今天终于要完成好久之前的一个约定了
~
在很久很久以前的
《如果风停了,你会怎样》
中,小夕提到了“深刻理解了
sigmoid
的同学一定可以轻松的理解用
(
假
)
深度学习训练词向量的原理”,今天就来测测各位同学对于
sigmoid
的理解程度啦
~
习惯性的交待一下前置铺垫:
1
、词袋模型、独热与词向量概念扫盲
2
、
sigmoid
到
softmax
(至关重要)
3
、逻辑回归
4
、逻辑回归到神经网络
总之,请务必清楚词向量的概念,深刻理解
softmax
的概念和公式内的意义。尤其是要理解
softmax
函数具有“
两向量的‘亲密度’转条件概率
”的功能:
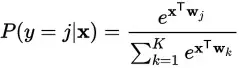

嗯。。。还是开篇扫盲一下。可能有的同学觉得是深度学习兴起之后才有的“词向量”,实际上,最早用来做词向量的模型并不是神经网络,而是更加传统的机器学习算法,如以线性代数中的
SVD
(奇异值分解)为核心
LSA
(隐性语义分析),还有后来的以贝叶斯理论为核心
LDA
(隐含狄利克雷分布,一种
NLP
中经典的主题模型)。
一方面,小夕下面要讲的确实是作为一种用神经网络(人们为了提高逼格,更喜欢叫用深度学习
xxx
)训练词向量的基本理论和方法,但是实际上,小夕并没有把它当神经网络看,因为理解了小夕讲的
softmax
后,这种方法不过是用了一下
softmax
而已,还不如叫“基于
softmax
分类器”或者“基于改良的逻辑回归”呢。。。当然啦,对外还是要称之为神经网络的。
首先,我们来想一下,凭什么可以训练出
《词向量概念扫盲》
中描述的这么棒的可以编码语义的词向量呢?其实呀,只要是用无监督的方法去训练词向量,那么这个模型一定是基于
“
词共现
”
(word co-occurrence)
信息来实现的。
设想一下,“萌”的语义跟什么最相近呢?有人会想到“可爱”,有人会想到“妹子”,有人会想到“小夕”(
\(//∇//)\
)。为什么呢?因为很大程度上,这些词会同时出现在某段文本的中,而且往往距离很近!比如“萌妹子”、“这个妹子好可爱”、“小夕好萌吖”。正是因为这种词共现可以反映语义,所以我们就可以基于这种现象来训练出词向量。
既然语义相近的两个词(即差别很小的两个词向量)在文本中也会趋向于挨得近,那如果我们可以找到一个模型,它可以在给定一个词向量时,计算出这个词附近出现每个词的概率(即一个词就看成一个类别,词典中有多少词,就是多少个类别,计算出给定输入下,每个类别的概率),那么训练这个模型不就把问题解决了嘛。是不是突然觉得
softmax
函数简直是为这个任务量身定做呐
~
我们就将词典大小设为
D
,用
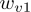 、
、
 、
...
、
...
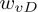 表示词典中的每个词。
表示词典中的每个词。
如下图:
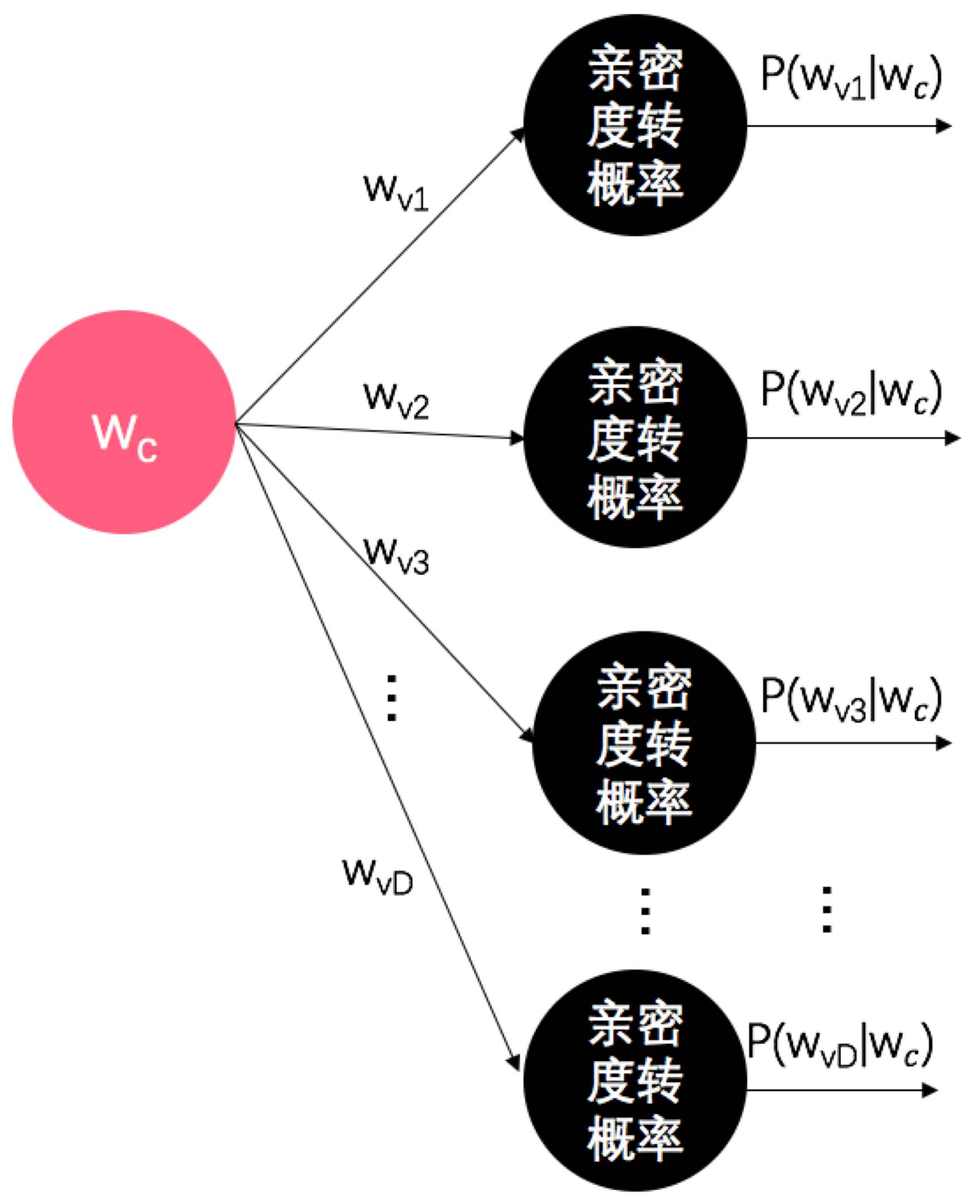
看,这不就是简单的
softmax
分类器嘛
~
所以这个
model
的假设函数就是简单的:
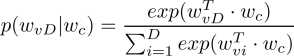
从这个
model
中也能看出,模型的输入不仅是输入,而且是其他输入的参数!所以这个
model
的参数是维度为
D*embed_dim
的矩阵
(每行就是一个用户定义的
embed_dim
大小的词向量,词典中有
D
个词,所以一共有
D
行),而且输入也是从这个矩阵中取出的某一行)。
假设函数有了,那么根据
《一般化机器学习》
,我们需要定义
损失函数
。当然,根据前面所说的词共现信息来定义啦。
为了好表示,我们将模型输入的词称为
中心词
(central word)
,记为
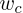 ,将这个词两边的词记为
目标词
(objected word)
,记为
,将这个词两边的词记为
目标词
(objected word)
,记为
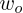 ,假如我们只将中心词附近的
m
个词认为是它的共现词(也就是中心词左边的
m
个词以及中心词右边的
m
个词),那么目标词一共有
2m
个,分别记为
,假如我们只将中心词附近的
m
个词认为是它的共现词(也就是中心词左边的
m
个词以及中心词右边的
m
个词),那么目标词一共有
2m
个,分别记为
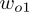 、
、
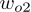 、
...
、
...
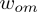 。(下文将会看到,在整个句子的视角下,
m
被称为
窗口大小
)
。(下文将会看到,在整个句子的视角下,
m
被称为
窗口大小
)
如果我们令
m=1
,那么对于下面这个
长度为
T=10
句子:
今天 我 看见 一只 可爱的 猫 坐 在 桌子 上。
那么当我们将“猫”看作中心词时,目标词就是“可爱的”和“坐”,即
今天 我 看见 一只 【可爱的 猫 坐】 在 桌子 上。
我们就认为这两个词跟猫的语义是相关的,其他词跟猫是否相关我们不清楚。
所以我们要争取让
P(
可爱的
|
猫
)
、
P(
坐
|
猫
)
尽可能的大
。
讲到这里,最容易想到的就是使用似然函数了。由于这里类别特别多,所以算出来的每个概率都可能非常小,为了避免浮点下溢(值太小,容易在计算机中被当成
0
,而且容易被存储浮点数的噪声淹没),更明智的选择是使用对数似然函数。所以对于一段长度为
T
的训练文本,损失函数即:
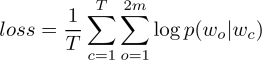
当然啦,这里要让长度为
m
的窗口滑过训练文本中的每个词,滑到每个词时,都要计算
2m
次后验概率。而每次计算后验概率都要用到
softmax
函数,而回顾一下
softmax
函数,它的分母是很恐怖的:
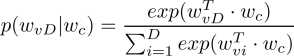
类别越多,分母越长。而我们这里类别数等于词典大小啊!所以词典有
10
万个单词的话,分母要计算
10
万次指数函数?所以直接拿最优化算法去优化这个损失函数的话,肯定会训练到天长地久(好像用词不当)。那怎么办呢?
一种很巧妙的方法是将原来计算复杂度为
D
的分母(要计算
D
次指数函数)通过构造一棵“
胡夫曼二叉树
(Huffman binary tree)
”来将原来扁平的“
softmax
”给变成树状的
softmax
,从而将
softmax
的分母给优化成计算复杂度为
log D
。这种树形的
softmax
也叫
分层
softmax(
Hierarchical Softmax
)
。
还有一种优化方法是
负采样(
Negative Sampling
)
,这种方法可以近似计算
softmax
的对数概率。对使用分层
softmax
和负采样优化模型计算复杂度感兴趣的同学,可以看下面这篇论文:
Mikolov,T., Sutskever, I., Chen, K., Corrado, G., & Dean, J. (2013, October 17).Distributed Representations of Words and Phrases and their Compositionality.arXiv.org
诶诶,说了这么多,这个看起来这么简洁优美的
model
叫什么名字呢?
它就是
Mikolov
在
2013
年提出来的
Skip-gram
(简称
SG
)
,这也是大名鼎鼎的开源词向量工具
word2vec
背后的主力
model
之一(另一个模型是更弱鸡的连续词袋模型,即
cBoW
)。
说些题外话,
SG
和
cBoW
是
Mikolov
在
2013
年的一篇论文中提出来的
(Mikolov, T.,Chen, K., Corrado, G., & Dean, J. (2013, January 17). Efficient Estimationof Word Representations in Vector Space. arXiv.org.)
并且在同一年,
Mikolov
又在更上面那篇优化
SG
计算复杂度的论文中开源了
word2vec
这个词向量工具,可谓是深度学习应用于自然语言处理领域的里程碑式的成果。当然啦,要说
NLP
的超级里程碑,还是要数
2003
年
Bengio
大神的这篇论文的,这也是词向量概念的鼻祖论文:
Bengio Y, Ducharme R,Vincent P, et al. A neural probabilistic language model[J]. Journal of machinelearning research, 2003, 3(Feb): 1137-1155.
关于在准确度表现上基本可以完爆
SG
和
cbow
的
model
,参考
GloVe
模型(
Global Vector
),有兴趣的同学可以看一下论文:
PenningtonJ, Socher R, Manning C D. Glove: Global Vectors for WordRepresentation[C]//EMNLP. 2014, 14: 1532-1543.
当然啦,建议在读之前先熟悉一下文首提到的LDA模型
,否则可能阅读有点难度哦。






