本文共分为四部分：生存分析的概念、生存分析的SPSS实践操作、生存分析的R语言实践操作，生存分析的在线工具介绍等四部分。欢迎转发收藏。
1、生存分析的概念
生存分析（survival analysis）是对生存时间进行分析的统计技术总称。
既考虑结果又考虑生存时间的一种统计方法，并可充分利用截尾数据所提供的不完全信息，对生存时间的分布特征进行描述，对影响生存时间的主要因素进行分析。
生存分析的基本目的就是刻画生存时间的分布。
生存分析相较于其它多因素分析的主要区别点：生存分析考虑到了每个研究对象出现某一结局所经历的时间长短。
（一）基本概念：
1.起始事件(initial event)：反应生存时间起始特征的事件，如疾病确诊、
某种 疾病治疗开始等。
2.失效事件(failure event)：在生存分析随访研究过程中，一部分研究对
象可 观察到死亡，可以得到准确的生存时间，它提供的信息是完全的，
这种事件称为失效事件，也称之为死亡事件、终点事件。
3.生存时间（survival time）：从规定的观察起点到某一特定终点事件出
现的时间长短。
其中根据研究对象的结局，生存时间数据可分为两种类型：
1)完全数据：在规定的观察期内，对某些观察对象观察到了终点事件发
生，从起点到终点事件所经历的时间，称为生存时间的完全数据
（complete data）。用符号“ t ”表示。
2)删失数据（截尾数据）：规定的观察期内，对某些观察对象，由于某种
原因未能观察到病人的终点事件发生，并不知道其确切的生存时间， 如
病人生存时间在未达到规定的终 点就被截尾一样，称为生存时间的删失
数据，又称截尾数据，用符号“ t+ ”表示。
产生删失数据的常见原因有：
1)研究结束时终点事件尚未发生；
2)失访；
3)死于其它原因；
4)由于严重药物反应而终止观察或改变治疗措施。
4.死亡概率（probability of death）：表示某单位时段开始存活的个体，在 该时段内死亡的可能性；如年死亡概率。
注意：如果年内有删失，则分母用校正人口数（有效数目）：
校正人口数 = 年初人口数—删失例数/2
5.生存概率（probability of survival） ：单位时段开始 时存活的个体，到该时段结束时仍然存活的可能性。（注意：若年内有删失，分母用校正人口数。）
6.生存率（survival rate） ：0 时刻存活的个体经历 tk时个单位时间段后仍存活的可能性。
1)若资料中无删失数据时：
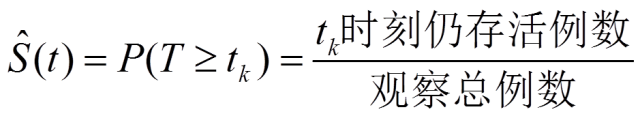
2)若资料中有删失数据，则须分段计算生存概率，再应用概率乘法定理将分时段的生存概率相乘得到生存率：
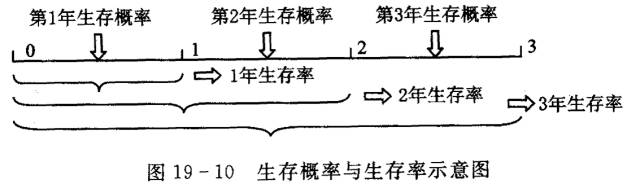
故生存率又称为累积生存概率（cumulative probability of survival )，它是随着时间的变化而变化着的，是关于时间的函数，称为生存函数（survival function）。
3)区分：生存率与生存概率
生存概率是针对单位时间而言的；
生存率是针对某个较长时段的，是生存概率的累计结果。
4)生存率的标准误：
其中：dj为第 j 个时间段内死亡人数；nj为第 j 个时间段期初人口数
5) 置信区间：
7. 中位生存期（median survival time） ：也称半数生存期，是生存时间中位数（M/P50），表示恰有50%的个体存活的时间，即生存率为50％时对应的生存时间，是描述集中趋势 指标。其中，中位生存期越长，表示疾病的预后越好。
8.生存期的四分位数间距： Q＝P75-P25
是反映离散程度大小的指标。
9.风险函数（hazard function）: t 时刻存活的个体在t 时刻的瞬时死亡率。
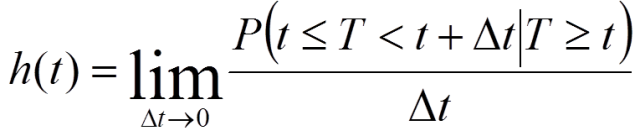h(t)近似地等于t 时刻存活的个体在此后一个单位时段内的死亡概率。
若h(t)是一种上升曲线，表示危险率随时间变化而增加，如患有急性疾病患者治疗无效其危险率随时间呈现增加趋势；
若h(t)是一种下降曲线，表示危险率随时间变化而减少；
若h(t)是一种稳定的危险率函数，则表示患者在稳定期，危险率基本不变。
10.生存曲线：以观察（随访）时间为横轴，以生存率为纵轴，将各个时间点所对应的生存率连接在一起的曲线图。
生存曲线是一条下降的曲线，分析时应注意曲线的高度和下降的坡度。平缓的生存曲线表示高生存率或较长生存期，陡峭的生存曲线表示低生存率或较短生存期。
（二）生存分析的特点：
1.生存资料特点：
1) 有结局和生存时间两个因变量;
2)生存时间分布不正态—非负且右偏;
3)可能含有删失数据（censor）
2.生存分析特点：
1)同时考虑结局和生存时间两个因变量;
2)可处理生存时间分布不正态的问题；
3)可处理删失数据。
3.处理删失/截尾数据时两种错误的做法：
错误1：只考虑确切数据，丢弃截尾数据（损失信息）；
错误2：将截尾数据当作确切数据处理（低估了生存时间的平均水平）。
4.在处理正偏态分布数据时两种错误的做法：
错误1：采用平均生存时间而不是采用中位生存时间来表示生存时间的平均水平。
错误2：采用常规 t 检验或方差分析进行组间比较。（应采用log-rank检验比较几组生存时间 ）
（三）绘制生存曲线方法：
大样本资料的生存分析方法—寿命表法（Life-table method）
2.小样本资料的生存分析方法：kaplan-meier法或称乘积极限法（product limit method）
并根据绘制出的生存曲线进行分析：Cox比例风险回归模型
常用工具：SPSS 、 R语言 、 SAS等。下节介绍。
2、生存分析-SPSS
常见方法有寿命表法、Kaplan-Meier分析法、Cox回归分析
一、寿命表分析
适用于大数据
示例：
若要研究性别对于肺病生存率有无区别，收集数据下列信息
time：生存时间（单位天）
status：0=存活，1=死亡
sex：1=男，2=女
操作步骤
按步骤将数据导入(lung数据集来自于R内置数据)
选定寿命表分析方法
对各选项进行设置（其中注意状态设置：选取表示事件已发生的值）
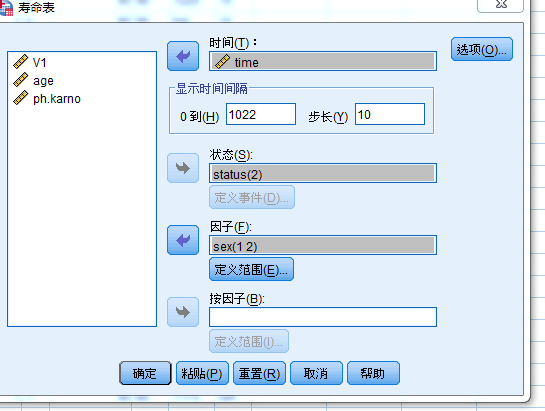
设置完所有选项后确认
得到结果（可进行导出）
1.得到存活表：该表给出了男女对应时间内存活和死亡人数，并计算了存活率、风险比等统计量
2.中位数生存时间：即生存率为50%时，生存时间的平均水平；
可知：生存时间的平均水平女士高于男士
3.生存函数：男士较女士累计生存率下降快
二、Kaplan-Meier分析
适用于小样本
示例：
若要研究药物治疗对卵巢癌生存率有无区别，收集数据下列信息
futime：生存时间（单位天）
fustat：0=存活，1=死亡
rx：1=未治疗，2=治疗
操作步骤：
按步骤将数据导入(ovarian数据集来自于R内置数据)
选定Kaplan-Meier分析法，并对选项进行设置
设置结束后确认
得到结果（可进行导出）：
1.生存表的均值和中位数、百分位数：可以看出治疗与未治疗有均值、四分位数略有差异
2.整体比较：检验结果p值>0.05,证明治疗组与非治疗组差异不显著
3.存活函数：治疗组较非治疗组生存结果好，但从假设检验结果来看差异不明显
三、Cox回归分析
示例:
若要研究结肠癌治疗方式对患者生存时间的影响，收集了下面所示的数据：
time：生存时间（单位天）
status：0=存活，1=死亡
rx：治疗方式，Obs=观察，Lev=方式1，Lev+5FU=方式2
obstruct：0=无阻塞的结肠肿瘤，1=有阻塞的结肠肿瘤
perfor：0=无结肠穿孔，1=有结肠穿孔
extent：传播程度：1 =黏膜下层,2 =肌肉,3 =浆膜,4 =相邻结构
操作步骤：
导入结肠癌colon数据（R中内置数据）
选定cox回归分析
参数设置：
协变量依次导入，方法按分析所需进行选择
点击"分类"，协变量依次选入分类协变量
点击"绘图"，勾选生存函数，主要变量为rx，将rx变量选入单线框中，绘制生存曲线
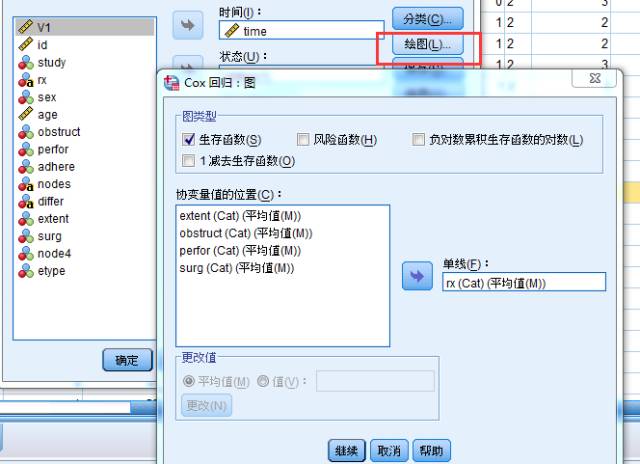
点击"选项"，设置输出RR的95%置信区间。
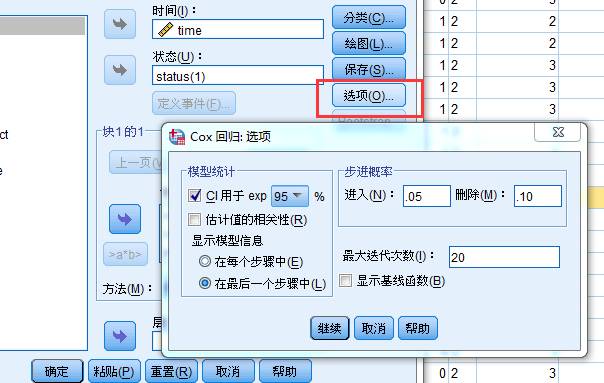
最后确定
得到结果（可导出）
1.案例处理摘要：1858个样本，其中920个死亡，938个存活，无缺失值存在
2.分类变量编码：分类变量编码方式及频数
3.拟合模型检验：原假设是“所有影响因素的偏回归系数均为0”，这里可以看出P<0.05拒绝原假设，认为有偏回归系数不为零的因素，值得进一步分析。
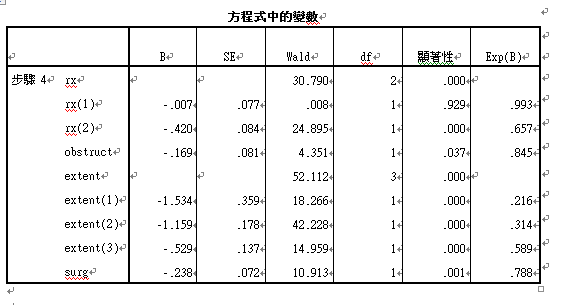
4.方程式中变量：多元回归结果，第二列B为偏回归系数，最后三列为OR值及其置信区间。
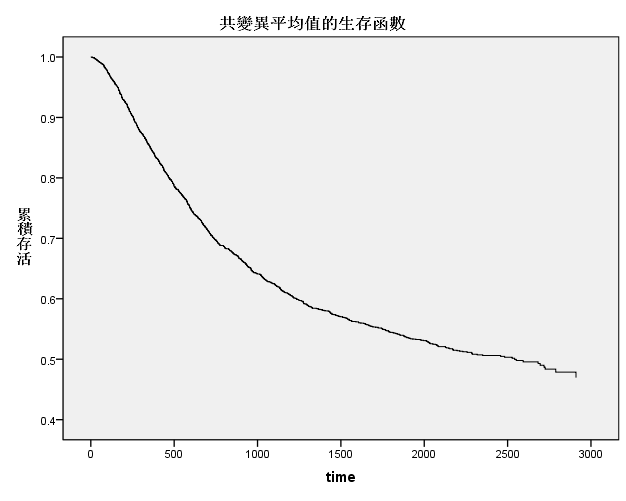
5.协变量均值处的生存函数：总体的生存函数。患者生存率下降较快
6.生存函数：在控制了其他变量后，有无治疗的生存函数对比，可以直观看出，接受Lev+5FU治疗的患者的生存情况优于未接受治疗Obs和接受治疗Lev的患者。
3、生存分析-R语言
生存分析方法分类
1.参数法：假定生存时间服从某个特定的分布，然后根据分布的特点对生存时间进行分析，常用方法有指数分布法、weibull分步法、对数正态回归分布法等。参数法通过估计的参数得到生存率的估计值，对于两组及多组的样本可根据参数估计对其进行统计推断。
早期应用于武器使用寿命的研究等。
2.非参数法：根据样本的顺序统计量对生存率进行估计，常用的方法有log-rank检验、似然比检验，对于两个及多个生存率的比较，其零假设为两组或多组总体生存时间分布相同，而不对其具体的分布形式及参数进行推断。
常用于随访资料医学研究。
3.半参数法：只规定了影响因素和生存状况间的关系，但是没对时间（和风险函数）的分布情况加以限定。
这种方法主要用于分析生存率的影响因素，属于多因素分析方法，起典型方法是cox比例风险模型。
Cox模型分析法以风险率函数作为应变量，以与生存时间可能有关的协变量或交互项作为自变量来分析生存率。
生存分析使用R包
install.packages("Survival")
library(survival)
survival包中自带数据集ovarian
head(ovarian)
futime fustat age resid.ds rx ecog.ps
1 59 1 72.3315 2 1 1
2 115 1 74.4932 2 1 1
3 156 1 66.4658 2 1 2
4 421 0 53.3644 2 2 1
5 431 1 50.3397 2 1 1
6 448 0 56.4301 1 1 2
其中包含生存时间futime、状态fustat、治疗组别rx、ECOG评分ecog.ps等信息
参数法——survreg()函数
survreg(formula, data, dist, subset)
参数解释：
formula形如Y~X1+X2+X3，但注意生存分析中的应变量Y通常为Surv()函数处理的生存时间；data是数据在R中的名字，subset可以对数据进行筛选。
dist为因变量的分布，包括weibull（weibull分布）、exponential（指数分布）、gaussian（伽马分布）、logistic（logistic分布）、loglogistic（对数logistic分布）和lognormal（对数正态分布）。
示例：
canshufasummary(canshufa)
Call:
survreg(formula = Surv(futime, fustat) ~ ecog.ps + rx, data = ovarian,
dist = "exponential")
Value Std. Error z p
(Intercept) 6.962 1.322 5.267 1.39e-07
ecog.ps -0.433 0.587 -0.738 4.61e-01
rx 0.582 0.587 0.991 3.22e-01
Scale fixed at 1
Exponential distribution
Loglik(model)= -97.2 Loglik(intercept only)= -98
Chisq= 1.67 on 2 degrees of freedom, p= 0.43
Number of Newton-Raphson Iterations: 4
n= 26
分析：p=0.43>0.05因此两条生存曲线分布无显著性差异
非参数法——survdiff()函数
survdiff(formula, data, subset, rho)
参数解释：
formula：形如Surv(time, status)~predictors；
data是数据在R中的名字，subset可以对数据进行筛选。
rho数量参数用以指定检验类型，0为log-rank法或Mantel-Haenszel法，1为Wilcoxon法，默认为0。
示例:
survdiff(Surv(futime,fustat)~rx,data=ovarian)
Call:
survdiff(formula = Surv(futime, fustat) ~ rx, data = ovarian)
N Observed Expected (O-E)^2/E (O-E)^2/V
rx=1 13 7 5.23 0.596 1.06
rx=2 13 5 6.77 0.461 1.06
Chisq= 1.1 on 1 degrees of freedom, p= 0.303
分析： p=0.303>0.05,两种治疗方式无显著性差异，所以两种对于卵巢治疗方式没有显著性差异
此外，我们还可以通过绘制其生存曲线来查看结果，所使用的函数为survfit():
示例：
feicanshuplot(feicanshu,col=rainbow(2),lty=1,xlab="生存时间/天",ylab="生存率",main="生存曲线")
legend("topright",c("rx=1","rx=2"),lty=1:2,col=rainbow(2))
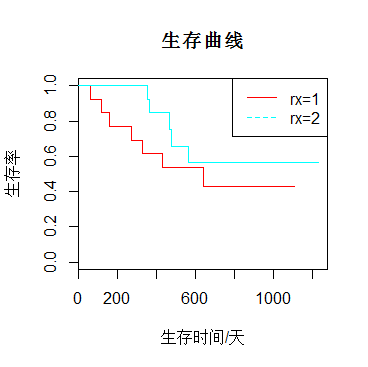生存曲线呈阶梯状：其中纵坐标为生存率，横坐标为生存时间，线上的短的竖线表示截尾值。
每一级阶梯代表一个死亡时间点(在结尾时间点无阶梯)；如果最大时间点是截尾则生存曲线不与曲线相交，否则与横轴相交。
半参数法——coxpy()函数
coxph(formula, data, subset)
参数解释：
formula，形如Y~X1+X2+X3+…+Xn，但Y必须为Surv()函数返回的结果;
data是数据集在R中的名称，subset可以对数据进行筛选
示例：
数据：pcb肝硬化数据
bancanshusummary(bancanshu)
Call:
coxph(formula = Surv(time, status) ~ sex + trt + ascites + hepato +
spiders, data = mydata)
n= 292, number of events= 125
(100 observations deleted due to missingness)
coef exp(coef) se(coef) z Pr(>|z|)
sexm 0.35806 1.43056 0.24070 1.488 0.136861
trt 0.05184 1.05321 0.18531 0.280 0.779660
ascites 1.65734 5.24533 0.25286 6.554 5.59e-11 ***
hepato 0.90319 2.46745 0.21273 4.246 2.18e-05 ***
spiders 0.65612 1.92729 0.19702 3.330 0.000868 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
exp(coef) exp(-coef) lower .95 upper .95
sexm 1.431 0.6990 0.8925 2.293
trt 1.053 0.9495 0.7325 1.514
ascites 5.245 0.1906 3.1955 8.610
hepato 2.467 0.4053 1.6262 3.744
spiders 1.927 0.5189 1.3099 2.836
Concordance= 0.762 (se = 0.028 )
Rsquare= 0.272 (max possible= 0.987 )
Likelihood ratio test= 92.83 on 5 df, p=0
Wald test = 111.7 on 5 df, p=0
Score (logrank) test = 145.8 on 5 df, p=0
分析：给出了风险比对数，风险比，标准误差，p值 ，风险比，置信区间和模型检验等信息
参数检验也基本表明，自变量ascites（腹水积液），hepato（肝肿大），spiders（皮肤血管畸形）对于结果有显著性影响(*表示显著程度)。
基本结果了解后，若要找到最佳模型，我们可以进行变量选择，这里采用逐步回归法进行分析
library(MASS)
bancanshu2
Start: AIC=1184.05
Surv(time, status) ~ sex + trt + ascites + hepato + spiders
Df AIC
- trt 1 1182.1
1184.0
- sex 1 1184.1
- spiders 1 1192.8
- hepato 1 1201.0
- ascites 1 1214.8
Step: AIC=1182.13
Surv(time, status) ~ sex + ascites + hepato + spiders
Df AIC
1182.1
- sex 1 1182.2
+ trt 1 1184.0
- spiders 1 1191.0
- hepato 1 1199.1
- ascites 1 1213.2
由最后结果可以知道，只包含变量ascites，hepato，spiders的模型是最佳模型。
summary(bancanshu2)
Call:
coxph(formula = Surv(time, status) ~ sex + ascites + hepato +
spiders, data = mydata)
n= 292, number of events= 125
(100 observations deleted due to missingness)
coef exp(coef) se(coef) z Pr(>|z|)
sexm 0.3568 1.4288 0.2407 1.483 0.138190
ascites 1.6417 5.1640 0.2465 6.659 2.75e-11 ***
hepato 0.9029 2.4669 0.2127 4.244 2.19e-05 ***
spiders 0.6584 1.9317 0.1970 3.342 0.000831 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
exp(coef) exp(-coef) lower .95 upper .95
sexm 1.429 0.6999 0.8915 2.290
ascites 5.164 0.1936 3.1852 8.372
hepato 2.467 0.4054 1.6258 3.743
spiders 1.932 0.5177 1.3130 2.842
Concordance= 0.756 (se = 0.027 )
Rsquare= 0.272 (max possible= 0.987 )
Likelihood ratio test= 92.75 on 4 df, p=0
Wald test = 111.9 on 4 df, p=0
Score (logrank) test = 145.8 on 4 df, p=0
绘制生存曲线：
plot(survfit(bancanshu2),col=c("black","darkred","darkgrey"),lty=1,xlab="生存时间/天",ylab="生存率",main="生存曲线")
legend("bottomleft",c("ascites","hepato","spiders"),lty=1:2,col=c("black","darkred","darkgrey"))
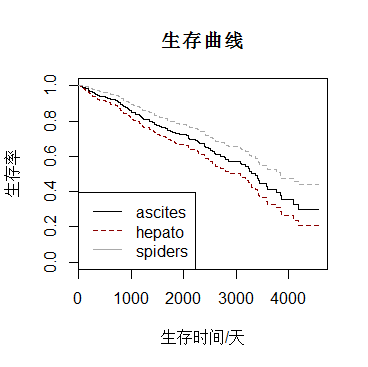
注：数据可能不恰当导致分析有所偏颇
4、生存分析——在线工具
生存分析除了采用R、SPSS等软件外，也可以应用在线工具
网址：http://kmplot.com/analysis/
下面简单介绍下这个在线工具KM plotter
打开界面：
KM plotter 应用一万余个癌症样本评估了五万多个基因对于生存的影响，其中样本来自于对乳腺癌、卵巢癌、肺癌、胃癌患者数十个月的随访，因此该网站可以进行乳腺癌、卵巢癌、肺癌、胃癌的mRNA表达和乳腺癌miRNA的预后分析。
下面以乳腺癌为例进行预后分析：
点第一个预选框进入breast canner的预后分析界面
1.输入Affy id 或者Gene symbol（例如：STAT2）
2.病人划分：中值、四分位值等（例如：median）
3.生存状态：RFS（无复发生存）、OS（总生存期）、DMFS（无病生存）、PFS（无进展生存）（例如RFS）
4.探针集合选项设置（例如：user selected probe set）
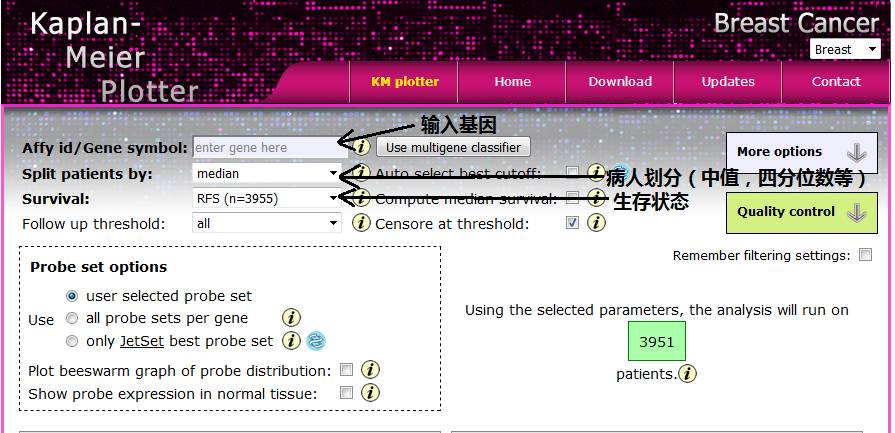
5.肿瘤分型设置
6.绘图
得到结果：
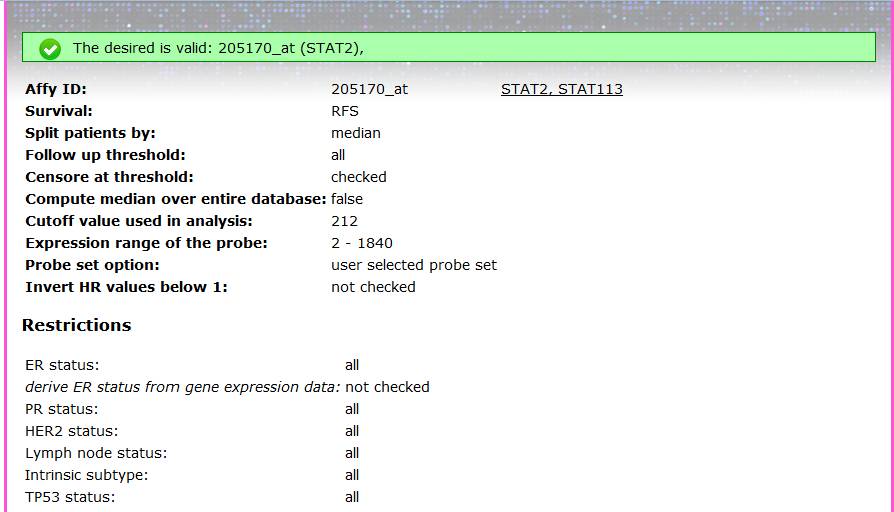
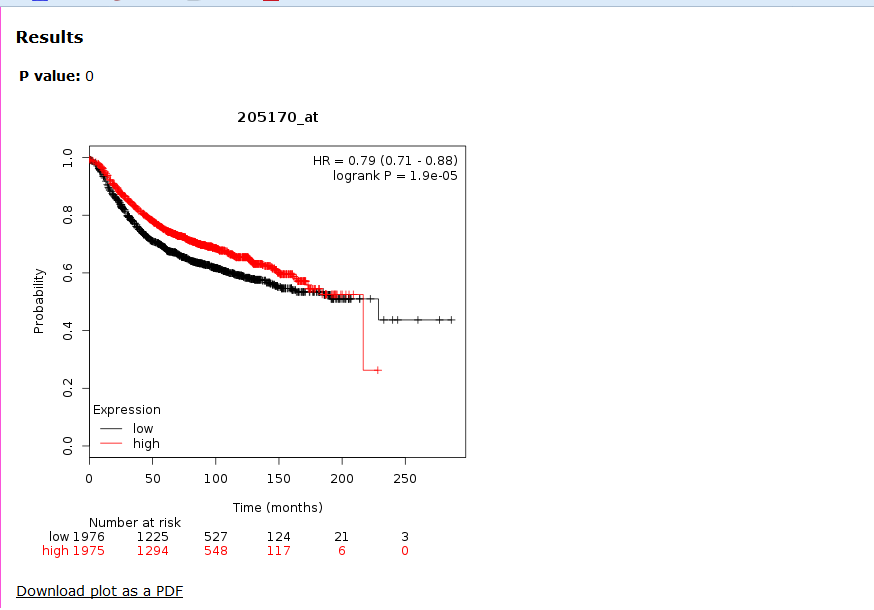
同理也可对其他癌症进行类似的预后分析并画出生存曲线。
欢迎留言补充其他工具。
