一分钟
记住走马灯数
作为数学系博士生，我常常告诉自己那些美丽有趣的自然数一定有它存在的意义，就像帅气逼人的超模君依然具有令人羡慕的才华。
但是，存在这么一些自然数，例如走马灯数一直被视为无用，一身正气的超模君决定找到它们的作用，为他们正名！
今天，超模君终于找到了它们的用处了，忍不住要跟模友分享！
142857，一个神奇的数字，最早发现于古埃及的金字塔内，是众多古埃及未解之谜之一。
为什么142857被称为走马灯数呢？根据超模君多年的分析经验，它一定与走马灯存在某种关系！
走马灯大家都知道吧，我们常常能在古装剧里面看到：
灯内点上蜡烛，烛产生的热力造成气流，令轮轴转动。轮轴上有剪纸，烛光将剪纸的影投射在屏上，图像便不断走动。因多在灯各个面上绘制古代武将骑马的图画，而灯转动时看起来好像几个人你追我赶一样，故名走马灯。
而142857的2~6倍的数，恰好存在着重新排列，你追我赶地这种走马灯的性质，所以也就被成为了走马灯数。
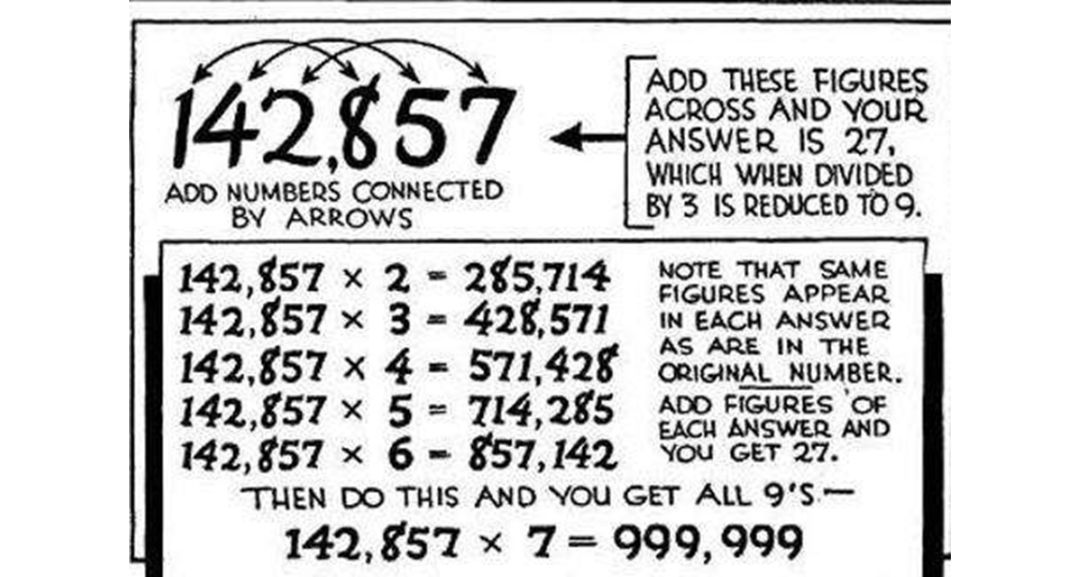
同时，它还证明了一周有七天，它的2~6倍所得结果是“124857”中的6个数字重新排列组合，依顺序轮值一次，到了7倍，它们就“放假”，结果为“999999”代班。
关于走马灯数有趣的还不止这些。前面说到了142857乘于7倍，结果为999999，那么7倍以后呢？
还有更有趣的平方拆和！
先平方，再拆解求和平方拆分后再加起来，又回到了142857的倍数。
关于走马灯数，还有很多有趣的规律，而超模君手机的开锁密码就在这些数字里面。
为了让广大模友也能用上这走马灯数，超模君决定传授大家一方法，一分钟记住走马灯数！
如何快速记住走马灯数？
第一步，记住142857，我们画一个圆，分成六份，依次把1、4、2、8、5、7按照顺时针排序，如图：
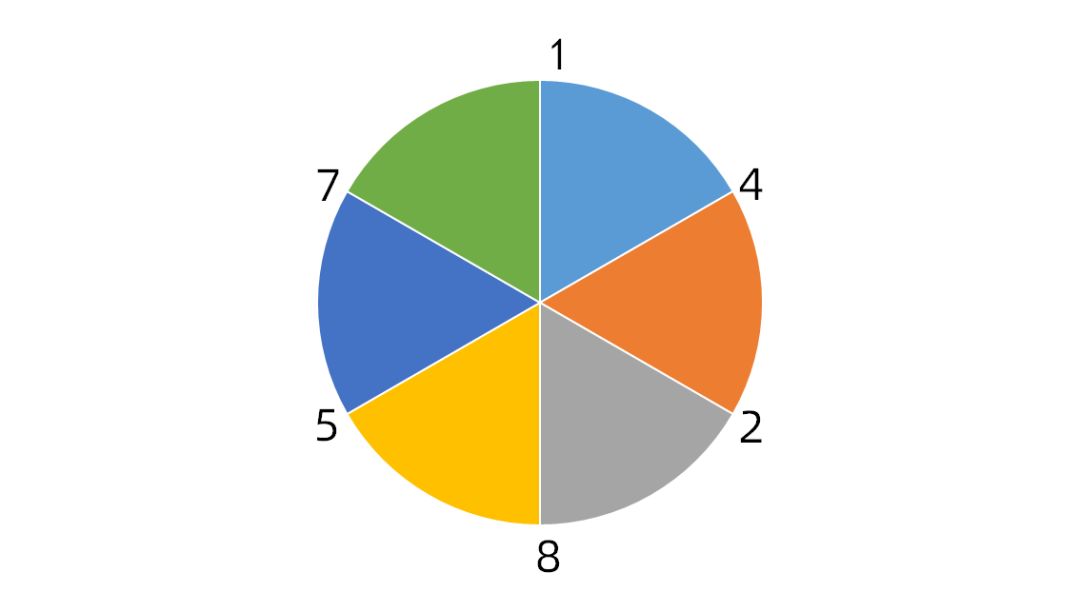
第二步，给142857从小到大依次标上序号（1~6），如图：
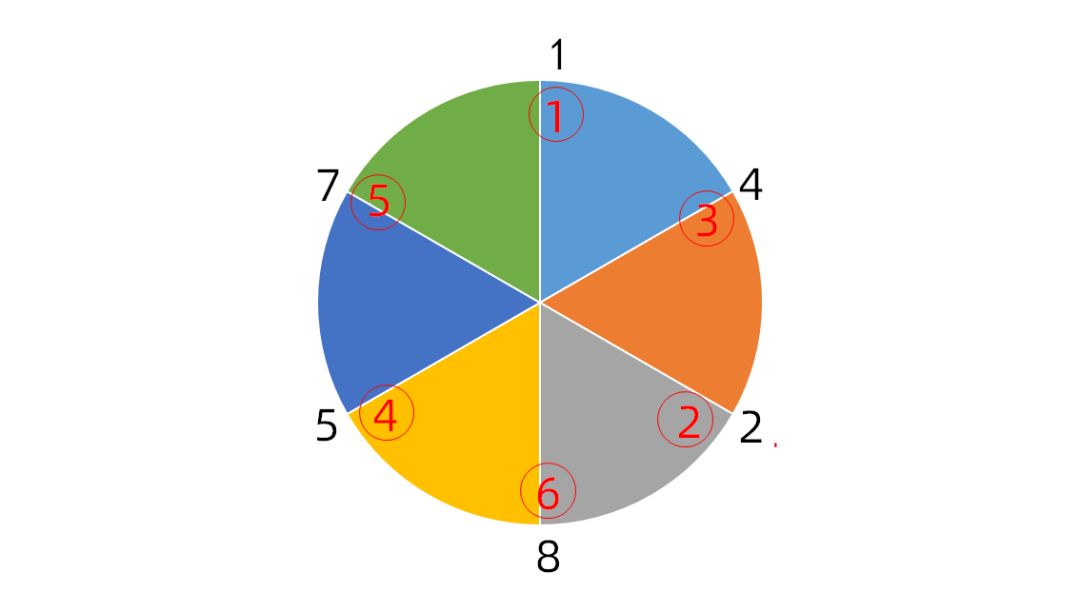
第三步，确定倍数，按顺时针数6个数，即可，例如2倍，结果是285714！如图：
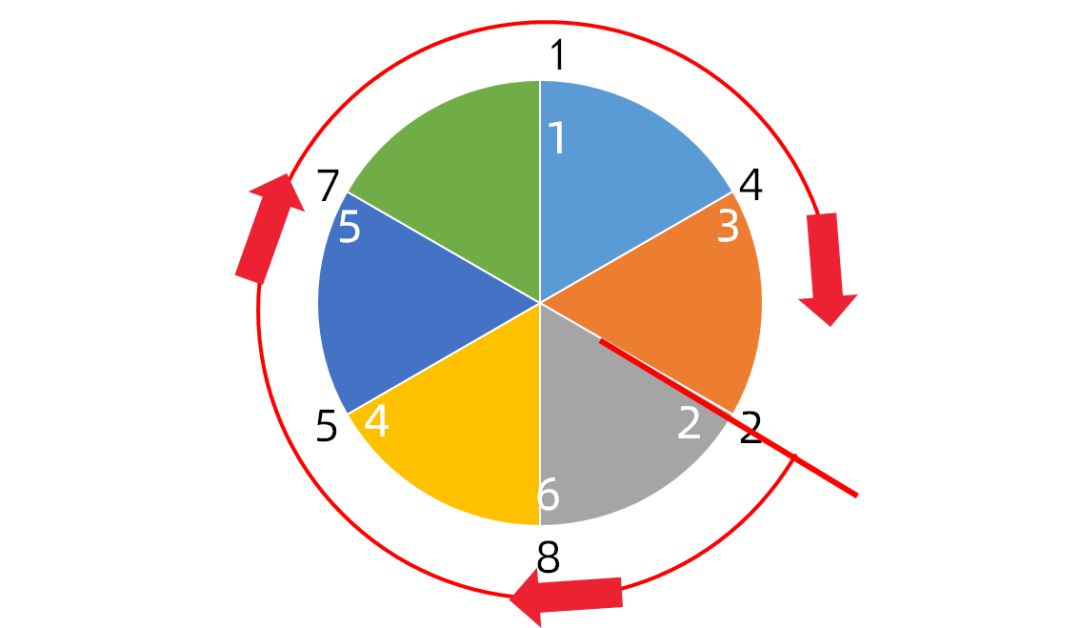
就这样，我们就可以快速把1~6倍的走马灯数拿下。
这个方法的关键是：记住第一个数142857，按顺时针排好位置即可！
一分钟记住走马灯数速成！
好了，记下了走马灯数，好学的模友会问，还有没有类似走马灯数这样的数字呀？
有，当然有！
比如说，缺“8”数。
9的平方是81，1/81=0.012345679...，在这个循环节中唯独缺少数字8，故称为“缺8数”。
“缺8数”正统的表示方法为：12345679，有许多奇妙的性质：
如
“清一色”
12345679*63=7777777
“三位一体”
12345679×12=148148148
12345679×15=185185185
12345679×57=703703703
......
还有“
回文数
”
如果一个自然数正着读和倒着读都一样，如121，32123等，叫回文数。
怎么得到回文数呢？
任意一个自然数，把它倒过来与原来的数相加，然后把这个和数与和数倒过来相加，一直重复这个运算，最后能得到一个回文数。
比如：
194+491=685
586+685=1271
1271+1721=2992
当然也有个别自然数目前还算不出回文数。比如说196这个数，按照上述变换规则重复了数十万次，仍未得到回文数。但是人们既不能肯定运算下去永远得不到回文数，也不知道需要再运算多少步才能最终得到回文数。
目前需要计算步骤最多的回文数需要261步计算，它是由一个19位数字1,186,060,307,891,929,990算出的。
再讲一个“雷劈数”
雷劈数也叫“分和累乘再现数”，又称卡普列克数，它被发现的灵感是来源于自然。
印度数学家卡普列克在一次旅行中，遇到猛烈的暴风雨，他看到路边一块牌子被劈成了两半：一半上写着30，另一半写着25。这时，卡普列克忽然发现30+25=55，55^2=3025，把劈成两半的数加起来，再平方，正好是原来的数字。
最小的奇雷劈数是81，最小的偶雷劈数是100。999，7777，9999，77778，22222，99999，142857，999999等等的平方数都是雷劈数。
关于有趣的自然数，我想应该是无穷无尽的，只是很多有趣的数还没有发现而已。
说了这么多有趣的数，它们有什么用呢？
很遗憾地告诉你，目前来说，它们在数学研究上没什么明显的实际作用。
但是它们长得好看，它们很美呀~
世间万物都有它存在的意义。
这些数既可以
