假说预警~~
具象的想象做不到，因为我们想象不出没有见过的世界。
比如我说，我有一只狗是绿色的。你说你没有见过，但是可以想象出来啊~
其实呢，狗你见过，绿色你也见过。你可以组合罢了。
但如果我说我有一只狗是你从没见过的“红橙黄绿青蓝紫黑白灰”之外的一个全新的颜色，你就傻眼了。因为你想象不出那个全新的颜色。
区别就在这里。
不过不要气馁，具象的想象无法进行，抽象的想象却是可以的。
我们可以用我们见过的东西，去构建一个类似的模型。
慢慢说，长文预警！！
让我们先从0维开始。什么是0维呢？可以理解为没有空间。
就像是一个点，一个想象出来的点。因为没有空间，所以它没有体积，没有大小。它即存在又虚无，空即是色，色即是空。本来无一物，何处惹尘埃。
那现在我们想象在它的右边出现了一个空间，这个点突然可以往右移动了。那么恭喜你，一维空间出现了。
一个点，从A移动到B，无论多长的距离，只要它动了。OK，这就是空间。
所以一维空间是一条线。而一个无限大的一维空间，就是一条无穷无尽，不知从哪里开始，也不知到哪里结束的直线。
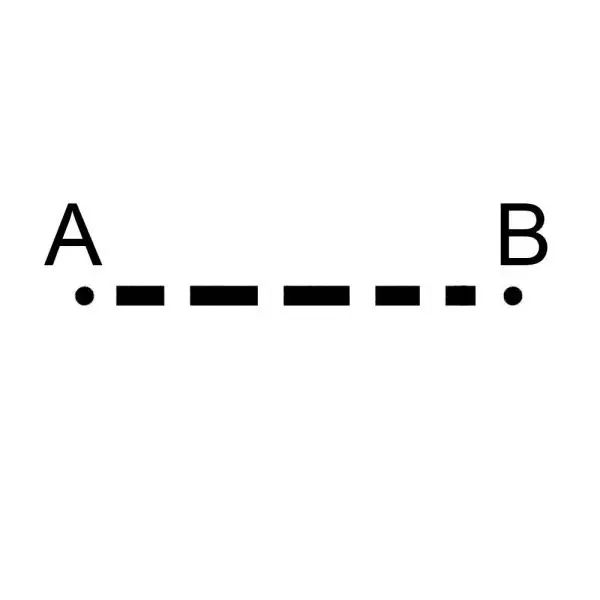
我们可以快速地进阶。现在想象一下有一个生物，它的概念里面只有长度，没有宽度。因为它生活在一维空间中，永远只能在一条直线上移动，左手右手一个慢动作……
比如一个一维空间的直线AB，假设A点是北京，B点是上海好了。
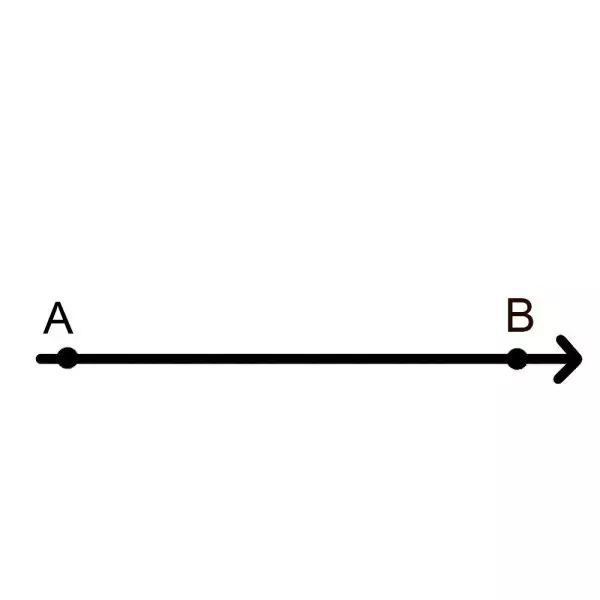
有一天这个空间在更高维度的空间，也就是二维空间上，发生了扭曲。变成了一个二维的图形，然后A点和B点重合了。
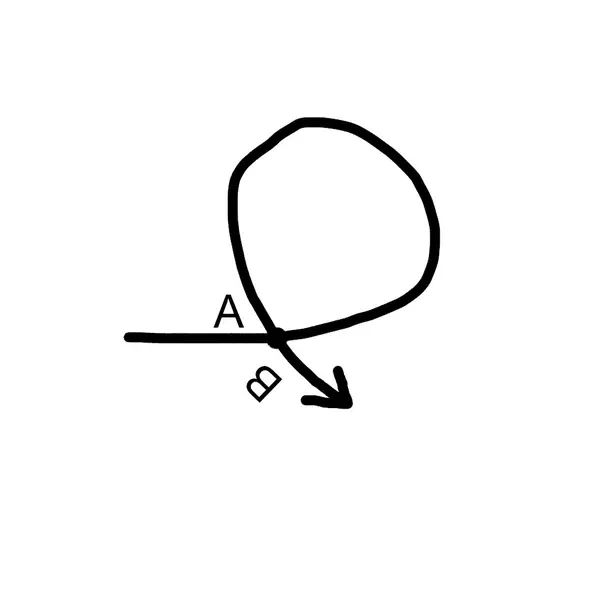
但是生活在直线上的一维生物并没有认知到二维。
那么在他们眼里世界发生了什么呢？有一个住在A点的人，他同时出现在了B点！A点B点都有他的存在，但是又只有一个他。于是所有人都为他献出膝盖，膜拜这个大神……
现在我们再进化到中学时期那个让我们无比头痛的平面几何中来。两条直线就能构成一个二维空间。
比如说直线X上的生物，X就是他们的世界。而对于直线Y上的生物来说，Y就是他们的世界。现在这两条直线在O点相会，于是就构成了一个二维的世界。
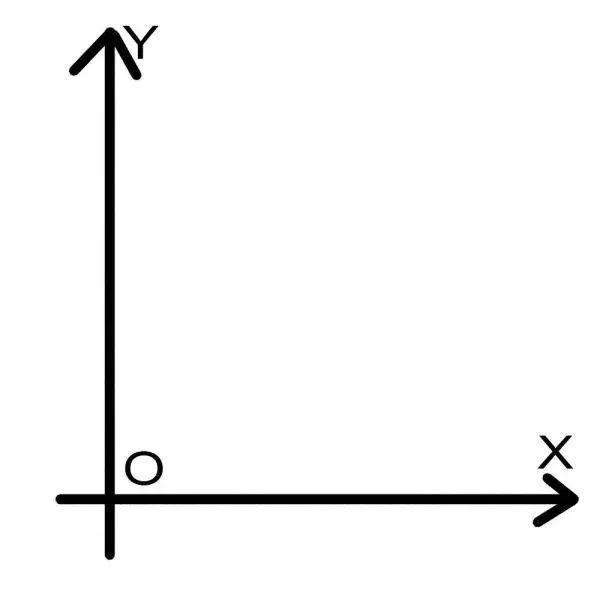
然后这些生物开始在二维空间过上了幸福的生活。
不过好景不长，一个三维空间的生物，突然沿着Z轴进入了这个平面。这哥们先在A点着陆，然后像一只鸟一样跳跃到了B点。这是一个在三维空间的运动。
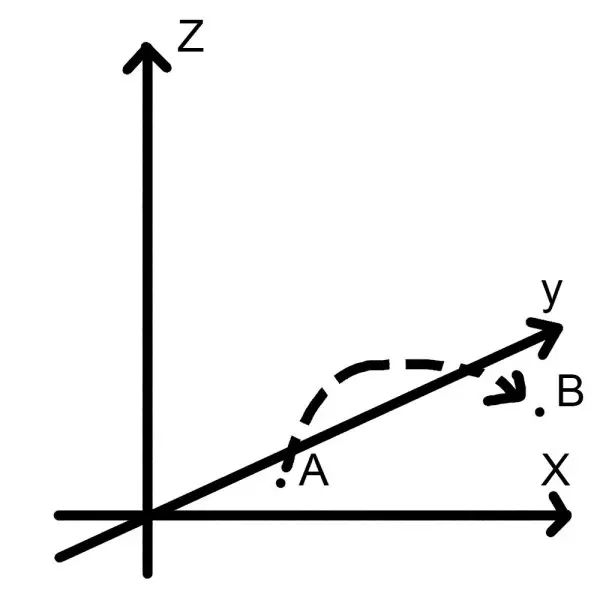
那么对于二维空间的人来说，这个家伙的运动意味着什么呢？
他从A点莫名其妙的消失了！然后又突然出现在了B点！二维空间的低等生物绞尽脑汁也想象不出这只鸟是怎么运动的，他们只能把这个三维空间的生物叫做不明飞行物，也就是UFO。
好了，从零维到我们熟悉的三维都很好理解。在我们开启第四维之前，首先得开一个脑洞，以便于更好的理解后面的维度。
接下来假说预警！！脑洞预警！！科幻预警！！玄学预警！！
如果你是严肃的物理党，请当作假说。如果你是普通的好奇党，请当作脑洞。如果你是严谨的数学党，出门左转……
让我们回到一维空间的直线X。现在假设这条直线从下往上运动，于是有了Y轴。
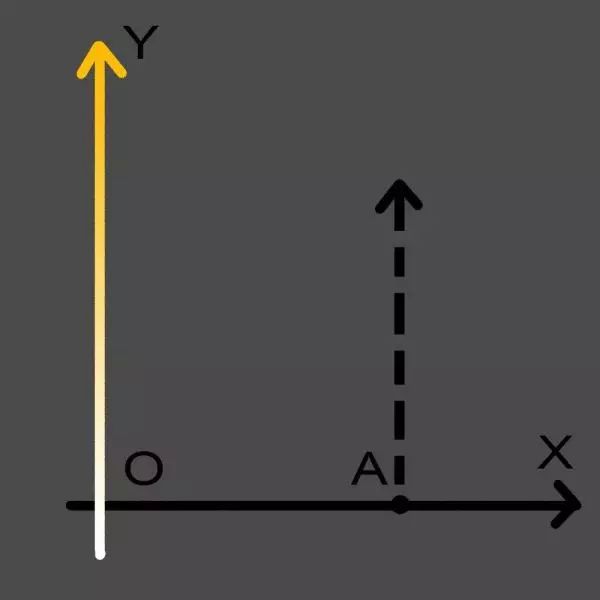
我们需要把Y轴涂成难看的黄白渐变色。
现在，生活在直线X上的低等生物A先生，它的世界还是一维空间，所以它认知不到一个完整的Y轴。
那条Y轴，在他的世界里永远都只是一个O点。
那么当X轴从下往上沿Y轴运动的时候，在A先生的眼里，左边的O点不是白色就是米色或者黄色。
所谓管中窥豹，所谓坐井观天。
OK，第一个脑洞开完，再回到我们最熟悉的三维空间。这个空间你可以想象成你的卧室，或者是整个宇宙，what ever，这不重要。
重要的是，我们现在要把你的卧室想象成一个点，排除掉暂时不虚要考虑的上下左右和前后。
那么如果我们的这个三维空间正沿着某一个轴运动的话，我们看到的就会如同A先生所看到的Y轴那样，一个白色的三维空间，慢慢地变成了黄色。
比如说你卧室里逐渐泛黄的墙壁，或者是窗外昼夜交替的天空。
也许这是一种比较好理解的方式。我们生活的三维空间，其实是在沿着一条线，从原点开始朝着固定的方向在运动。我们可以把这条维度理解为时间t。
物理学里面，可以把时间t轴作为一条维度去和其他的XYZ轴一起运算，并且在运算的过程中还可以和另外三条维度相转化。那这不是另一条维度是什么呢？
以至于很多抽象的宇宙模型都把时间作为一个维度去分析，不过它又不能等价于欧氏几何的维度。它很特殊……
简单一点说吧，我们的三维世界可以理解为一个漂浮在河水上面的落叶，大河向东流，天上的星星参北斗……而这条河的名字叫做时间。
不过它和其他的体积维度不同。我们没有能力逆流而上，而是只能沿着t轴的一个方向，从过去向未来运动着。
反观我们这些三维生物，对于这样一个高维度的认知，就如同刻舟求剑。
比如著名的双缝实验：
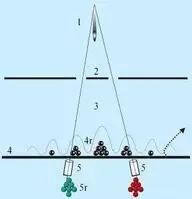
我们朝一个双缝发射一枚光子或者电子。按照传统的粒子观点，它要不走左边，要不走右边。
虽然我们用各种不同的实验，都无法观测到最终那个确定的结果。不过所有的实验观测都还是间接地指向了那个假想，这枚粒子同时穿过了两条缝。
它没有把自己一分为二，而是在那一时刻，它即在A缝，又在B缝。并且依然是一个完整的个体！
什么意思呢？科学家也不知道。
但是我们可以从空间的角度开一个脑洞。
假设一个情景好了。现在有一个一维的点，它在二维的直线上面相对于我们以光速飞行，从A点到B点。
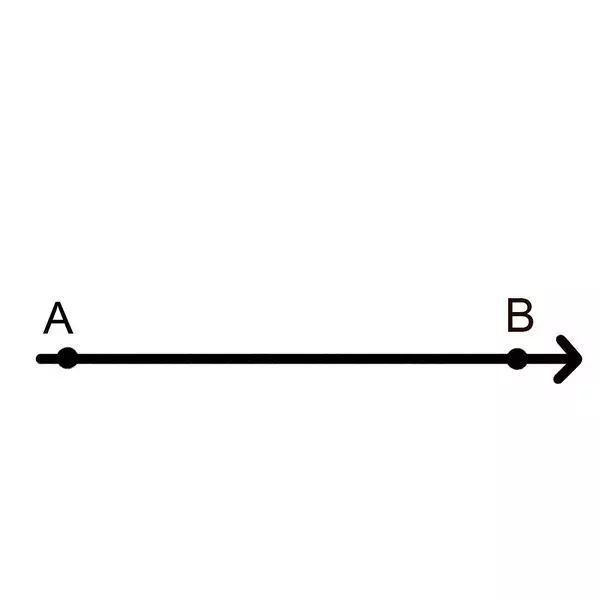
尽管理论上光速飞行做不到，但是我们可以畅想一下。
那么按照相对论，这家伙的时间相对于我们就静止了。也就是说，如果这家伙12:00从A点出发，同样是12:00就到达了B点。
同一个时刻，它处在A点到B点的每一个点上。
相对于我们在t轴上一分一秒地运动的生物来说，他在t轴上静止了。
结果就是一个零维的点，现在变成了一条一维的线。它升维了……
by the way……我没有说双缝实验的电子就是在以光速运动……这里只是提供一种如果。
再换一个脑洞好了。
我们现在需要把我们生活的三维空间想象成一条线。上下前后忽略掉暂时不需要考虑。
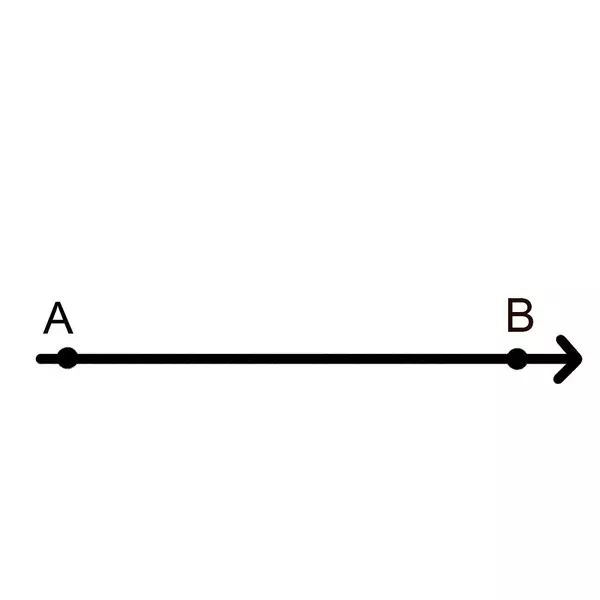现在，比方说A是左边的缝，B是右边的缝好了。
如果我们熟悉的三维空间，在更高维度中扭曲了，会发生什么呢？
是的，那个即在A点存在又在B点存在的神一般的哥们又出现了。
那这个空间通过扭曲进入的那个新的维度，可能是时间。
但是……但是了啊！！
这个扭曲的高维度，也可能是另外的维度哦～
于是我们的思想就进入t轴之外的，某一条维度。
还是要把我们的三维空间想象成卑微的一个点。我们沿着时间轴t，从A点出发。
假设A点是午夜十二点好了，然后我们一起等待凌晨一点钟的来临。这是四维空间。
那么有没有可能存在两个时间轴，比如t1和t2呢？
我们或者按部就班地沿t1轴走到B1点，也可能不走寻常路，沿着另外一条时间轴t2，走到B2点。
那么我们就可以在一个小时后之后到达B1，也可能在同样一个小时后到达B2。
B1和B2都是凌晨一点，却是两个不同的世界。
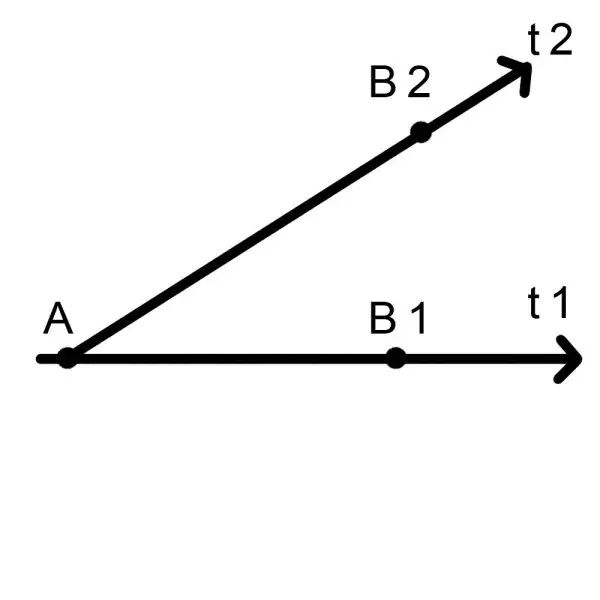
这是不是就是传说中的五维空间呢？
而第五条维度，专业一点的人叫它“速率指向”。拓展到宏观上面，通俗一点的话……我们给它起个名字吧，反正至今仍然没有确切的结果。
我们姑且叫它……“可能性”？
may be。
简单地说，宏观地说。现在不是粒子，是你。你曾经有两个选择，一个是成为工程师，另一个是成为会计师。如果你选择走T1的话，你就是工程师。而如果你选择走T2，那么你就是一个会计师。
于是乎，对于一个生活在五维空间的生物A的话。他就能同时看到那个工程师的你，以及会计师的你。
这个脑洞深入下去会变得更加诡异。我们还是把三维空间想象成一个点。那么四维空间就是一条直线。
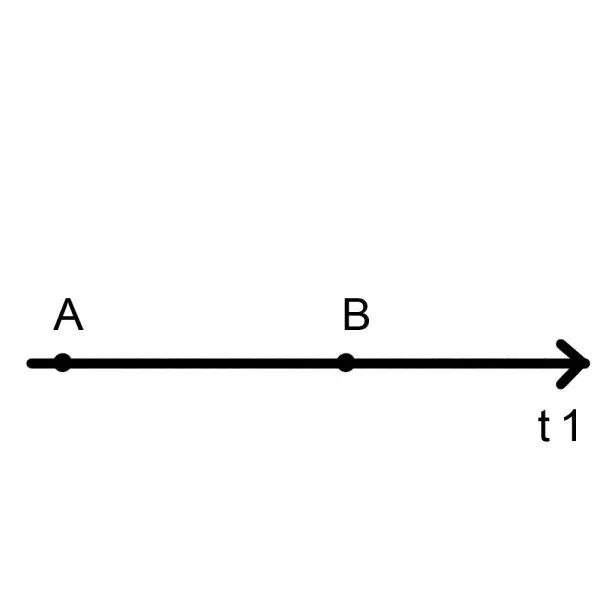
A点是你出生的时间，B点是你死亡的时间。
现在我们把t1轴扭曲一下，A点和B点在更高维度也就是五维空间里面重合了。
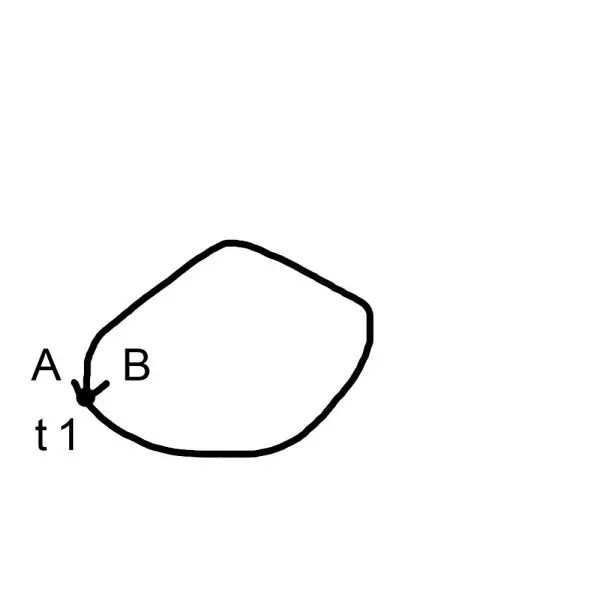
那么此时的你，就同时处在A点和B点。
你此时既处于A点的生存状态，又处于B点的死亡状态……
你看，大名鼎鼎的薛定谔的猫来了。
事情是这样的。量子物理学家们发现，某一个电子，在被某种射线照射的情况下，有一定概率被激发出来，也有一定概率不被激发出来。
这和我们一般理解的概率不一样，这枚电子的状态不是或，而是且！就像是一枚硬币，它既是正面朝上同时又是反面朝上！这是一种没有因的结果。只不过我们观测不到而已。
牛逼的来了。
这枚电子，它同时处于激发与不激发这样矛盾的，神一般的存在！
反常识吧？著名物理学家薛定谔也觉得这个理论太他妈扯淡了吧。甚至包括爱因斯坦也表示质疑。比如那句“上帝不会抛骰子”的话……
然后呢，薛定谔给出了一个反例。或者说悖论。
他假设有这样一个仪器：如果这枚电子激发出来，那么这个仪器就发出毒气，毒死一只猫。反之如果这枚电子没有被激发，那么就不发出毒气，喵星人依然欢快地活着。
那么，你们这些量子物理学家所说的电子处于即激发并且又不激发的情况。是不是等于在说，这只猫现在处于即活着，同时又死了的状态呢？
你们确定不是猴子请来的逗逼吗？
然而量子物理学家们也很无奈啊，他们认为通过实验结果，得到的推论就是这样啊！
然后这个脑洞今天成为了量子力学的入门小故事……
其实双缝实验也好，薛定谔的猫也好。我们今天也不确定这些实验和高维度到底有多少联系，只不过他们的现象和我们关于高维空间的脑洞如此类似。。。
比如说。。。我们回到双缝实验中来，见证一个更加更加更加诡异的奇迹。
激发一枚电子或者光子，前方有个双缝AB。我们通过一系列复杂的实验仪器来检测它到底走A还是走B。比如量子擦除实验。
实验比较复杂，我也记不住……
总之，我们如果开启这个仪器，这枚电子就无耻的不让我们测量它的粒子性了！然后我们就无法知道它到底是走A还是走B！
如果我们不开启这个复杂的实验系统，它就老老实实的保留它的波粒二象性。但如果我们开启了这个复杂的仪器，它就羞羞地压抑自己的天性，只表现波性或者只表现粒子性！
这枚粒子就像是有思想一样，它在干扰我们的实验。
也就是说，在我们现有的水平上。如果我们没有测量它，推导结果就是它同时处于A和B的位置。但如果我们去测量它到底是走A还是走B，它就改变实验结果！“塌缩”为确定的A或者B。
而且我们无法观察到这个过程到底是怎样的。
什么意思呢。。。
回到我们的主题高维空间来。
现在有一个三维生物O，羞耻的被我们视为了一个点。
然后有代表第四维度的时间轴t1和t2。
这样两条t轴就构成了一个五维空间。
为了方便我们想象，这个五维空间被视为一个平面。
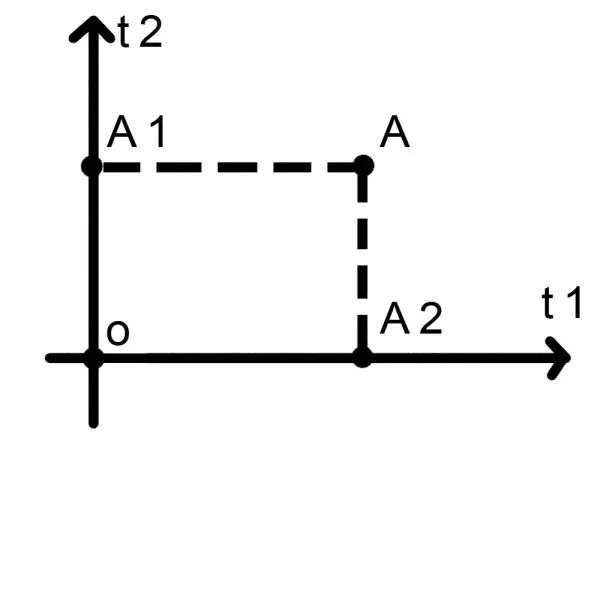
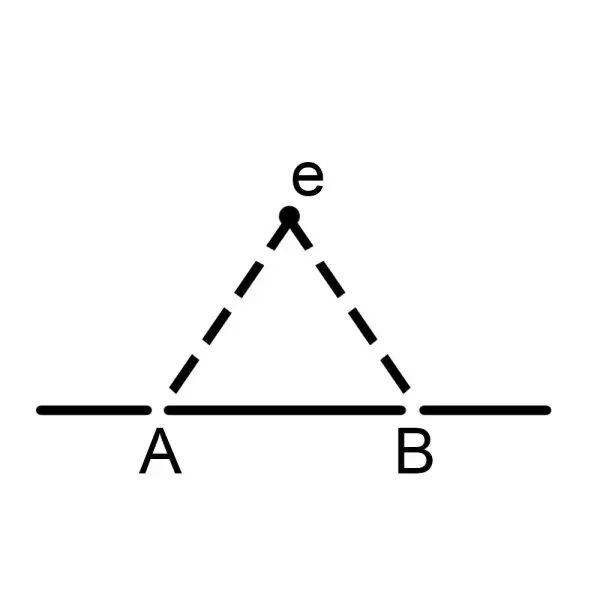
那么接下来，一个四维生物：“e”，就应该是一条直线。如图：
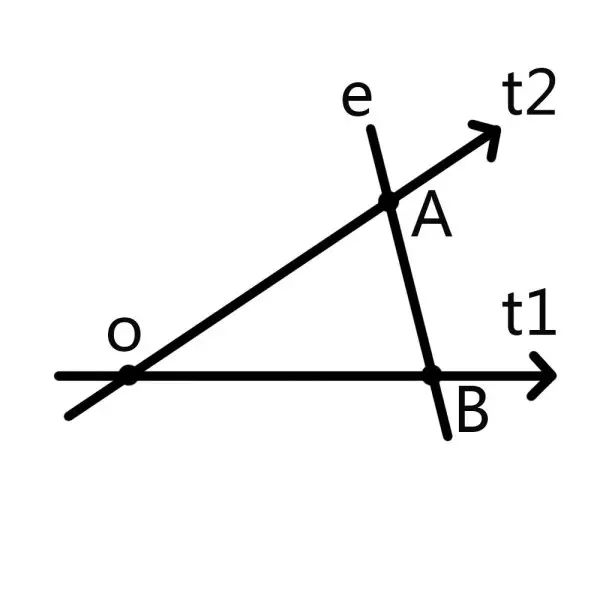
现在四维的e，在这个五维空间里面就和t1，t2各有一个交点A&B。那么同样是一点钟，在t1上它是B状态，但是在t2上它是A状态。
这两个状态都存在，但是我们这些愚蠢的三维生物只能苟且地观察到一种状态……非A即B。
因为我们只能在这条四维的直线上观察。
假设我们不服，试着在同一个时间去观察AB两种状态的话，e就会“塌缩”到我们的三维空间来，成为我们世界中那个确定的A点或B点中的一个。而另外一个遥远的交点，它依然存在，只不过是在高维空间中。
世界上最远的距离不是生与死的距离，而是你就在我身边我却不知道——泰戈尔
就像是薛定谔的猫，如果我们打开那个仪器，猫就要么活着要么狗带。但如果我们不打开那个仪器的话，猫就是生并且死的状态。
还是莎士比亚说得好啊。To be or not to be，thats a question……
你看question来了吧。那么answer是不是就是：电子和光子其实就是生活在高维空间的物体呢？
不知道……
因为以上的所有解释都只是假想而已。仅仅是我们试着用想象中的高维空间来解释那些粒子实验中反常识的现象。但是法治社会，我们却没有证据……
爱因斯坦自称证明了时间轴的存在，我们姑且相信他老人家。
不过很遗憾的，目前还没有实验及观察能证明在时间之外，第五条维度的存在。
其实我们甚至连真正的一维二维空间，都没有见过！
所以，上面的一切，从零维到所有维！都只是没有证据的假说。
说白了就是科学家自己编的一套理论，仅仅是在逻辑和概念上成立而已。并没有得到验证。
好了不要累觉不爱。。。至少我们还可以继续在逻辑和概念上，再开启一下六维空间。
还是一个低等的三维生物，自觉地被我们视为卑微的一个点。
假设在下图A点的时候，上帝抛了一枚硬币。走t1的话他就当工程师，走t2的话他就当会计师。
多出来的这个人生的岔路口就形成了一个五维空间。
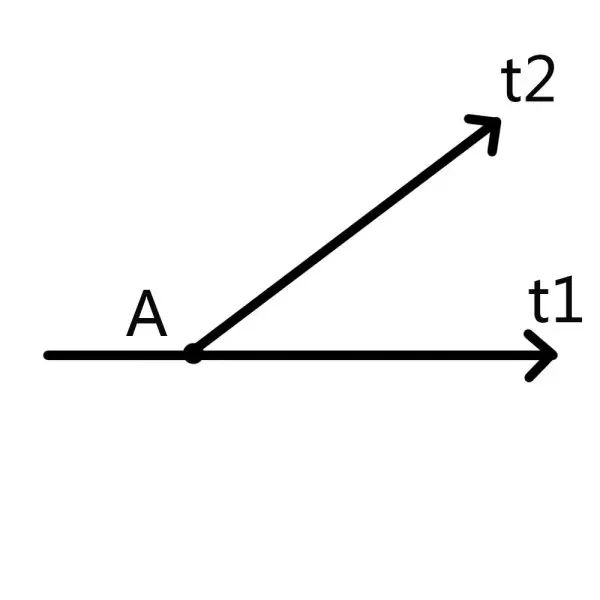那么问题来了，这个岔路口只能从这个方向长出来吗？如果上帝抛的不是一枚硬币，而是一个骰子呢……
比如这样：
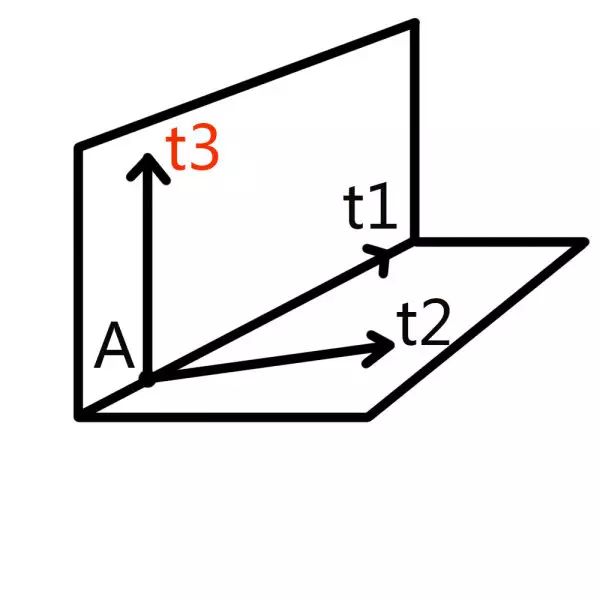
那这大概就是我们对于六维的理解。
依然是所谓的“速率指向”，不过我们刚才起了个更通俗的名字叫做“可能性”。
他还是你的各种可能，比如警察，比如黑社会。然后有一个胖子跟你说，路怎么走，你自己选。最后你说你还是想做一个好人……
但是这些都在第六维中。
接下来还是不要深入了……
因为在你看完上面的内容，并且接受了一切反常识的现象之后。
我们似乎可以继续把六维空间再视为一个点，那么它再继续沿一个未知的轴移动，那就是第七个维度。具体我就不展开了。
总之这里面有无数个你，无数次出生又无数次死亡。然后他们不是你的可能，他们是确定的另外一个你。
你可能是工程师，可能是会计师。他们也可能是工程师师，或者会计师。不过那些工程师也好会计师也罢，并不是六维空间的你，却依然是七维空间的你。。。
慢慢体会……不要绞。
那么现在我们完全可以在另外的方向再来一条直线啊，就像五维到六维的过程一样。那这不就是周杰伦的专辑《八度空间》了吗？
八维空间终于来了，一切却并没有结束。我们完全可以再把它视为一个点啊，然后再来一条直线代表九维空间，就这样无限叠加下去……
宇宙是不是就是这样无限叠加下去的无限维度呢？
答案依然是不知道……
虽然现在有大师自称找到了十一维。但是很难说这个构想将来会有怎样的变化。
所以呢……如果你和我一样，并不是一个专注于基础理论的孜孜不倦的学者，那么就停留在卑微的三维好了。
☞ 哈尔莫斯：怎样做数学研究
☞ 扎克伯格2017年哈佛大学毕业演讲
☞ 线性代数在组合数学中的应用
☞ 你见过真的菲利普曲线吗？
☞ 支持向量机(SVM)的故事是这样子的
☞ 深度神经网络中的数学，对你来说会不会太难？
☞ 编程需要知道多少数学知识？
☞ 陈省身——什么是几何学
☞ 模式识别研究的回顾与展望
☞ 曲面论
☞ 曲面论（第二讲）
☞ 曲面论（第三讲）
☞ 自然底数e的意义是什么？
☞ 如何向5岁小孩解释什么是支持向量机（SVM）？
☞ 华裔天才数学家陶哲轩自述
☞ 代数，分析，几何与拓扑，现代数学的三大方法论
算法数学之美微信公众号欢迎赐稿
稿件涉及数学、物理、算法、计算机、编程等相关领域。
稿件一经采用，我们将奉上稿酬。
投稿邮箱：[email protected]
