
本文来自作者
耀升
在
GitChat
上分享「常见的七种排序算法解析」,
「
阅读原文
」查看交流实录
「
文末高能
」
编辑 | 乔巴
1. 选择排序
实现原理
首先从未排序序列中找到最小的元素,放置到排序序列的起始位置,然后从剩余的未排序序列中继续寻找最小元素,放置到已排序序列的末尾。所以称之为选择排序。
代码实现

案例分析
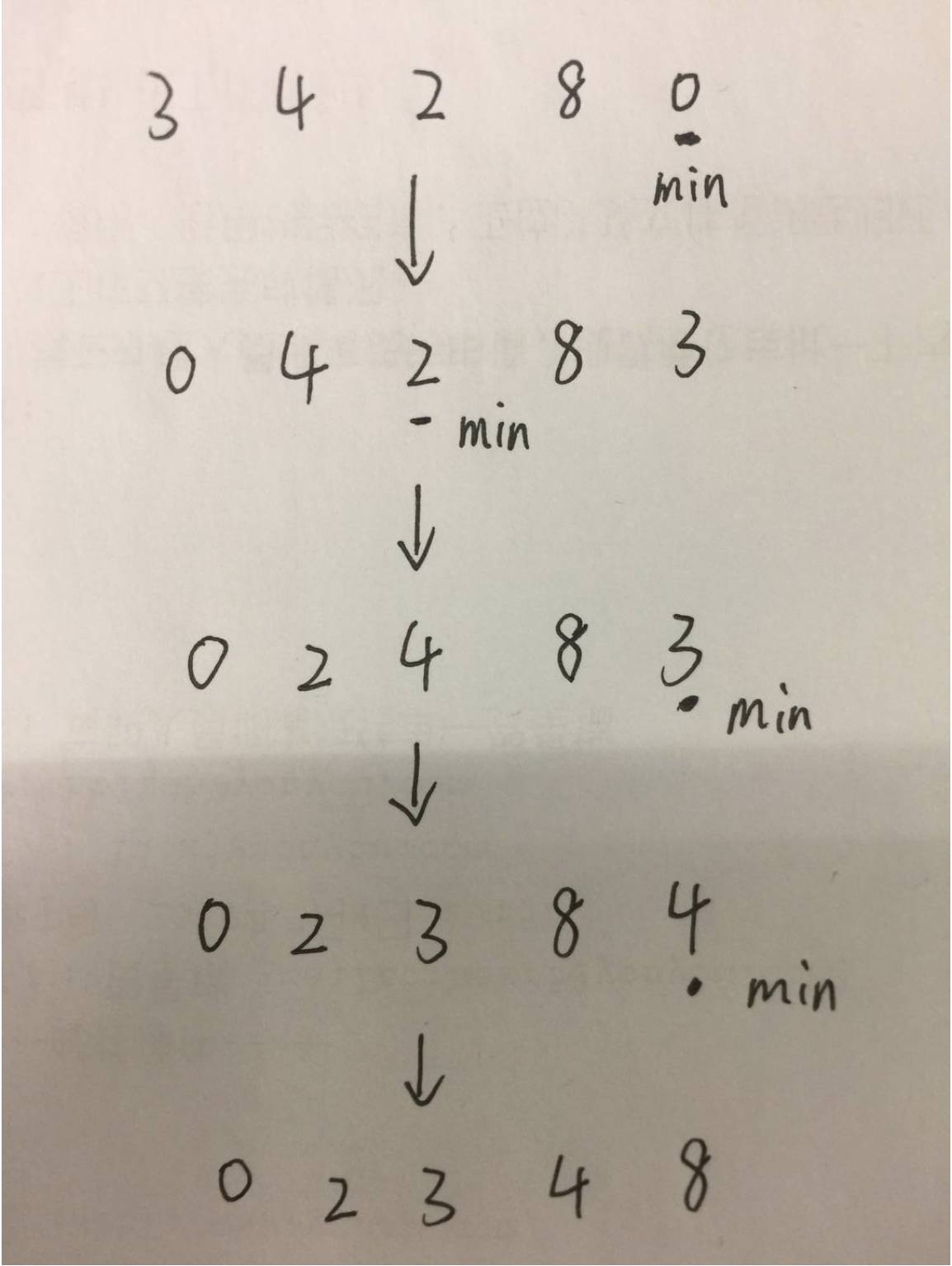
时间复杂度与空间复杂度
每次要找一遍最小值,最坏情况下找 n 次,这样的过程要执行 n 次,所以时间复杂度还是 O(n^2)。空间复杂度是 O(1)。
2. 快速排序
实现原理
-
在数据集之中,选择一个元素作为”基准”(pivot)。
-
所有小于”基准”的元素,都移到”基准”的左边;所有大于”基准”的元素,都移到”基准”的右边。这个操作称为分区 (partition)。
操作,分区操作结束后,基准元素所处的位置就是最终排序后它的位置。
-
对”基准”左边和右边的两个子集,不断重复第一步和第二步,直到所有子集只剩下一个元素为止。
代码实现

案例分析
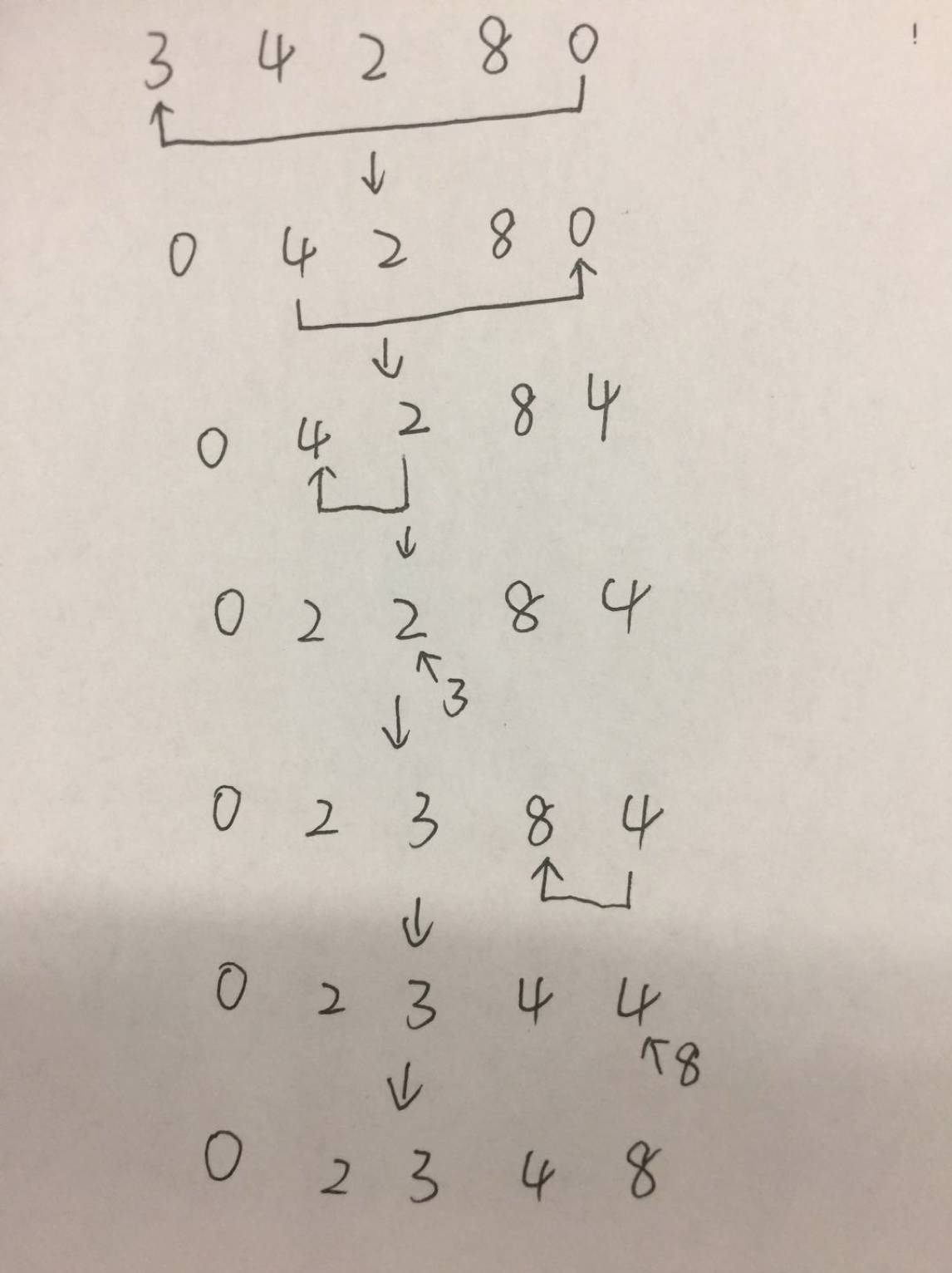
时间复杂度与空间复杂度
快速排序也是一个不稳定排序,平均时间复杂度是 O(nlogn)。空间复杂度是 O(logn)。
3. 冒泡排序
实现原理
依次比较相邻的两个元素,如果第一个元素大于第二个元素就交换它们的位置。这样比较一轮之后,最大的元素就会跑到队尾。然后对未排序的序列重复这个过程,最终转换成有序序列。
代码实现

案例分析
以数组 arr = [3 4 2 8 0] 为例说明,加粗的数字表示每次循环要比较的两个数字:

时间复杂度与空间复杂度
由于我们要重复执行n次冒泡,每次冒泡要执行n次比较(实际是1到n的等差数列,也就是 (a1 + an) * n / 2),也就是 O(n^2)。 空间复杂度是O(1)。
4. 插入排序
实现原理
代码实现

原理图解
案例1
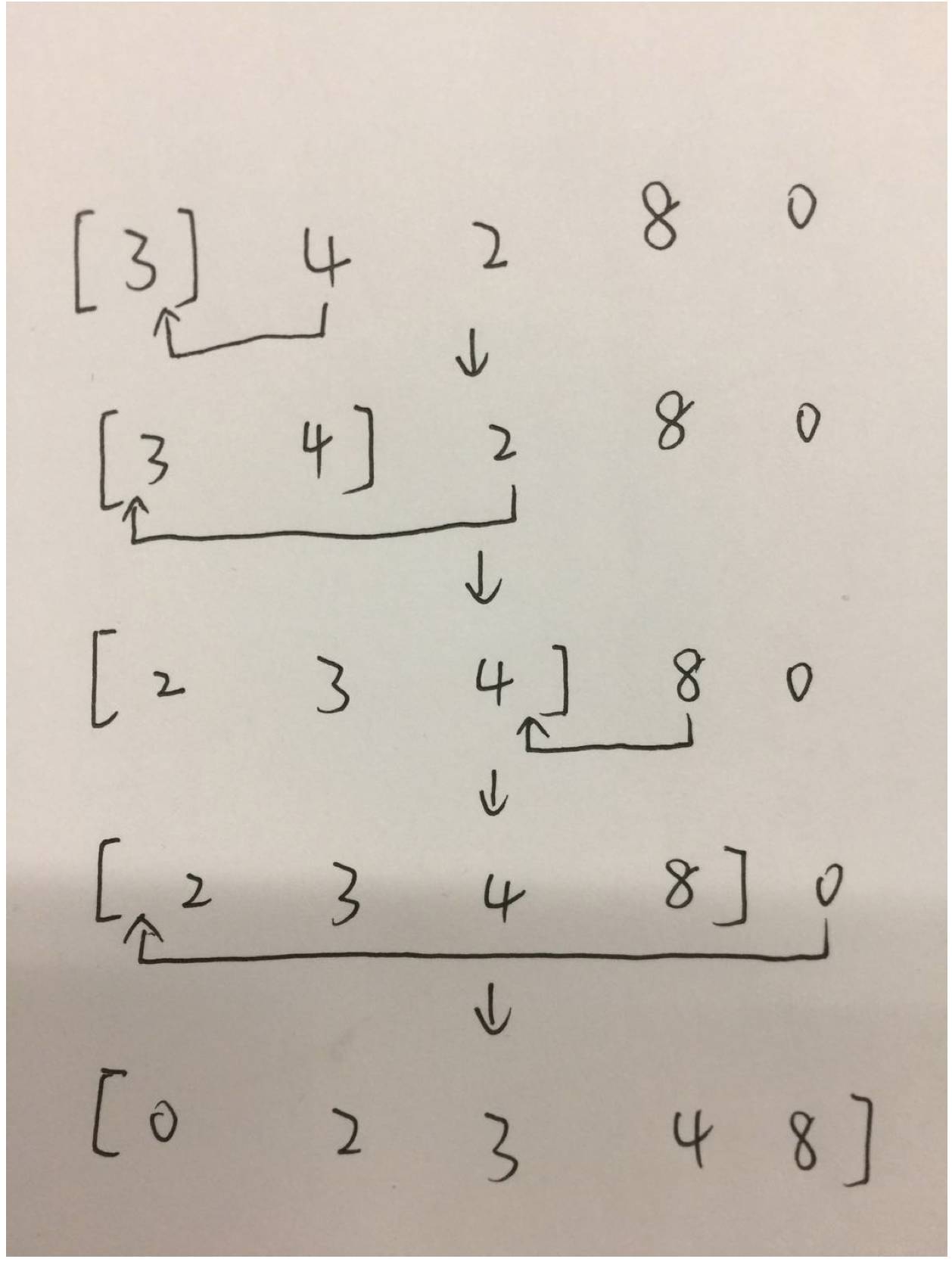
案例2
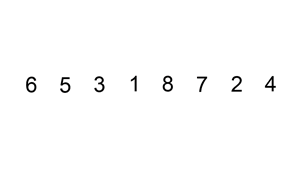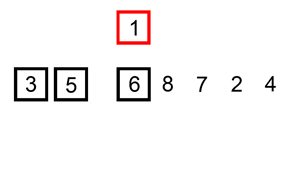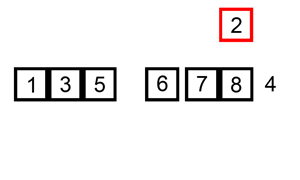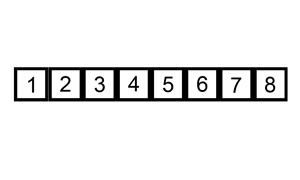
时间复杂度与空间复杂度
因为要选择 n 次,而且插入时最坏要比较n次,所以时间复杂度同样是 O(n^2)。空间复杂度是 O(1)。
5. 希尔排序
实现原理
代码实现

案例分析
假设有数组
array = [80, 93, 60, 12, 42, 30, 68, 85, 10]
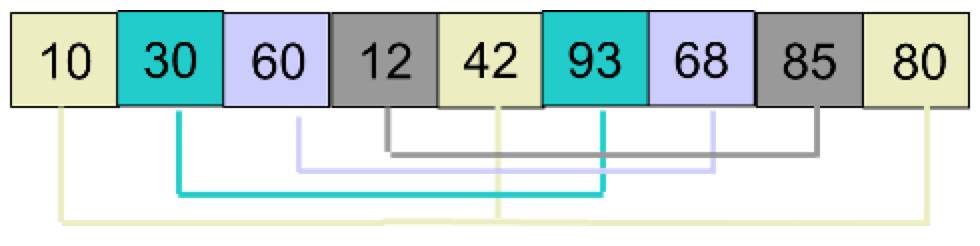
,首先取 d1 = 4,将数组分为 4 组,如下图中相同颜色代表一组:
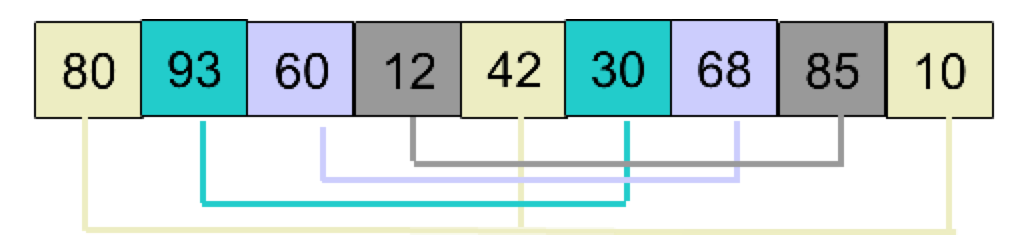
然后分别对 4 个小组进行插入排序,排序后的结果为:
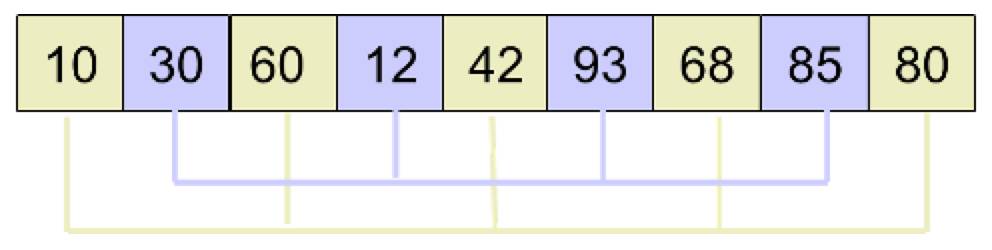
然后,取 d2 = 2,将原数组分为 2 小组,如下图:
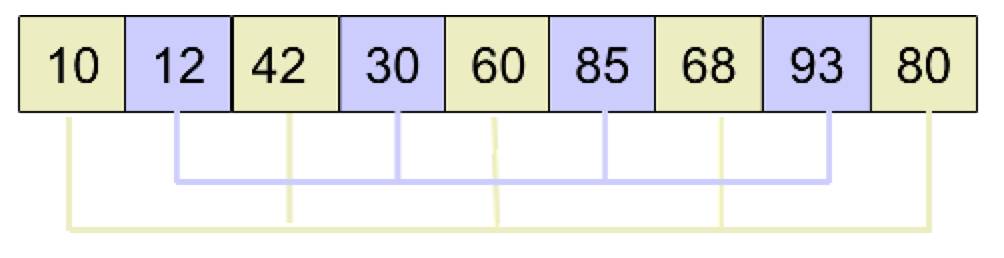
然后分别对 2 个小组进行插入排序,排序后的结果为:
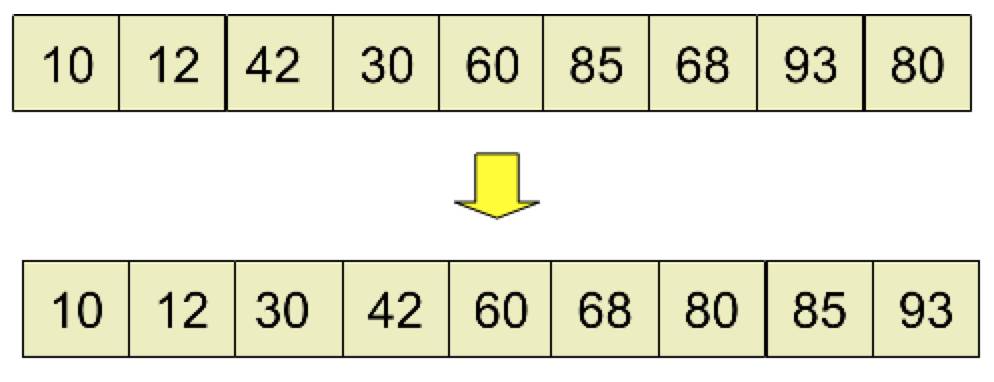
最后,取 d3 = 1,进行插入排序后得到最终结果:
时间复杂度与空间复杂度
希尔排序的时间复杂度受步长的影响,平均时间复杂度是 O(n log2 n),空间复杂度是 O(1)。
6. 归并排序
实现原理
总而言之,归并排序就是使用递归,先分解数组为子数组,再合并数组。
代码实现
public static int[] mergeSort(int[] arr){
int[] temp =new int[arr.length];
internalMergeSort(arr, temp, 0, arr.length-1);
return temp;
}
private static void internalMergeSort(int[] a, int[] b, int left, int right){
//当left==right的时,已经不需要再划分了
if (left
案例分析
案例1
以数组
array = [4 2 8 3 5 1 7 6]
为例,首先将数组分为长度为 2 的子数组,并使每个子数组有序:

案例2
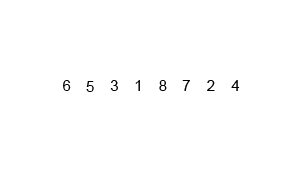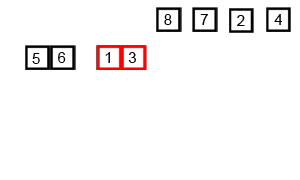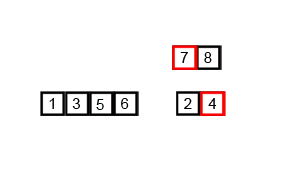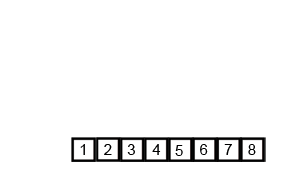
时间复杂度与空间复杂度
在合并数组过程中,实际的操作是当前两个子数组的长度,即 2m。又因为打散数组是二分的,最终循环执行数是 logn。所以这个算法最终时间复杂度是 O(nlogn),空间复杂度是 O(1)。
7. 堆排序
实现原理
堆排序就是把最大堆堆顶的最大数取出,将剩余的堆继续调整为最大堆,再次将堆顶的最大数取出,这个过程持续到剩余数只有一个时结束。在堆中定义以下几种操作:













