The receptive field is
perhaps one of the most important concepts in Convolutional Neural
Networks (CNNs) that deserves more attention from the literature. All of
the state-of-the-art object recognition methods design their model
architectures around this idea. However, to my best knowledge, currently
there is no complete guide on how to calculate and visualize the
receptive field information of a CNN. This post fills in the gap by
introducing a new way to visualize feature maps in a CNN that exposes
the receptive field information, accompanied by a complete receptive
field calculation that can be used for any CNN architecture. I’ve also
implemented a simple program to demonstrate the calculation so that
anyone can start computing the receptive field and gain better knowledge
about the CNN architecture that they are working with.
To
follow this post, I assume that you are familiar with the CNN concept,
especially the convolutional and pooling operations. You can refresh
your CNN knowledge by going through the paper “A guide to convolution
arithmetic for deep learning [1]”. It will not take you more than half
an hour if you have some prior knowledge about CNNs. This post is in
fact inspired by that paper and uses similar notations.
The fixed-sized CNN feature map visualization
The receptive field is defined as the region in the input space that a particular CNN’s feature is looking at (i.e. be affected by).
A receptive field of a feature can be fully described by its center
location and its size. Figure 1 shows some receptive field examples. By
applying a convolution C with kernel size k =3x3, padding size p = 1x1, stride s = 2x2 on an input map 5x5, we will get an output feature map 3x3 (green map). Applying the same convolution on top of the 3x3 feature map, we will get a 2x2 feature
map (orange map). The number of output features in each dimension can
be calculated using the following formula, which is explained in detail
in [1].
Note
that in this post, to simplify things, I assume the CNN architecture to
be symmetric, and the input image to be square. So both dimensions have
the same values for all variables. If the CNN architecture or the input
image is asymmetric, you can calculate the feature map attributes
separately for each dimension.
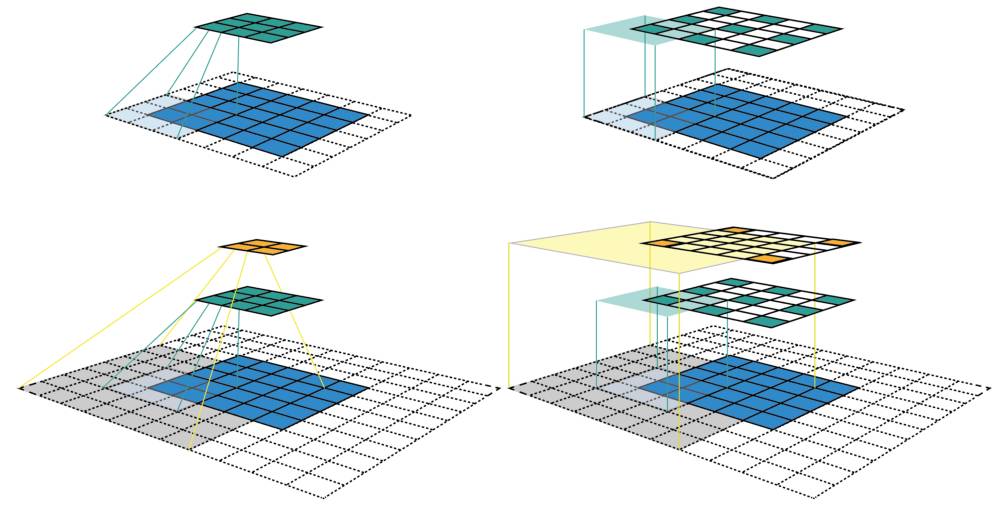
Figure
1: Two ways to visualize CNN feature maps. In all cases, we uses the
convolution C with kernel size k = 3x3, padding size p = 1x1, stride s =
2x2. (Top row) Applying the convolution on a 5x5 input map to produce
the 3x3 green feature map. (Bottom row) Applying the same convolution on
top of the green feature map to produce the 2x2 orange feature map.
(Left column) The common way to visualize a CNN feature map. Only
looking at the feature map, we do not know where a feature is looking at
(the center location of its receptive field) and how big is that region
(its receptive field size). It will be impossible to keep track of the
receptive field information in a deep CNN. (Right column) The
fixed-sized CNN feature map visualization, where the size of each
feature map is fixed, and the feature is located at the center of its
receptive field.
The left column of Figure 1
shows a common way to visualize a CNN feature map. In that
visualization, although by looking at a feature map, we know how many
features it contains. It is impossible to know where each feature is
looking at (the center location of its receptive field) and how big is
that region (its receptive field size). The right column of Figure 1
shows the fixed-sized CNN visualization, which solves the problem by
keeping the size of all feature maps constant and equal to the input
map. Each feature is then marked at the center of its receptive field
location. Because all features in a feature map have the same receptive
field size, we can simply draw a bounding box around one feature to
represent its receptive field size. We don’t have to map this bounding
box all the way down to the input layer since the feature map is already
represented in the same size of the input layer. Figure 2 shows another
example using the same convolution but applied on a bigger input
map — 7x7. We can either plot the fixed-sized CNN feature maps in 3D
(Left) or in 2D (Right). Notice that the size of the receptive field in
Figure 2 escalates very quickly to the point that the receptive field of
the center feature of the second feature layer covers almost the whole
input map. This is an important insight which was used to improve the
design of a deep CNN.
Figure
2: Another fixed-sized CNN feature map representation. The same
convolution C is applied on a bigger input map with i = 7x7. I drew the
receptive field bounding box around the center feature and removed the
padding grid for a clearer view. The fixed-sized CNN feature map can be
presented in 3D (Left) or 2D (Right).
链接：
https://medium.com/@nikasa1889/a-guide-to-receptive-field-arithmetic-for-convolutional-neural-networks-e0f514068807
原文链接：
http://weibo.com/1785748853/EDjvmvu04?from=page_1005051785748853_profile&wvr=6&mod=weibotime&type=comment#_rnd1491560422638
