今天我想讲四个应用,它们看起来很不相关,但是我会讲讲它们是怎样连在一起 的,特别是你可以用图来表示不同的应用。我会介绍一些机器学习里比较前沿的方法,那就是怎么把图表示成向量的结果。
 第一个应用是关于材料科学,或者是应用到药品的设计方面。
第一个应用是关于材料科学,或者是应用到药品的设计方面。
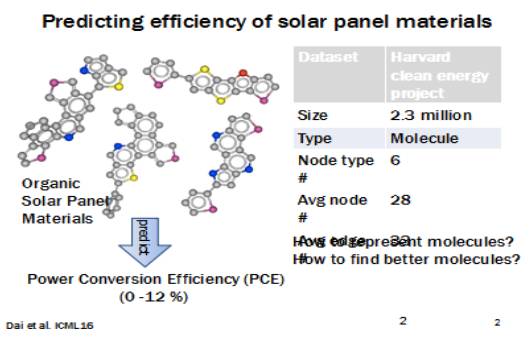
这个材料是一些分子结构,每一个节点都是不同的原子。显然它能通过图的形式联结在一起,问题就是分子的空间很大,怎么寻找有用的分子去制药,或者去做很好的材料?如果用机器学习的方法做,那么怎样去学习表达这 些分子结构,怎样通过这些表达的特征来学习一个非常好的预测模型,从而帮你找到很好的药物。
 第二个应用是关于推荐系统。
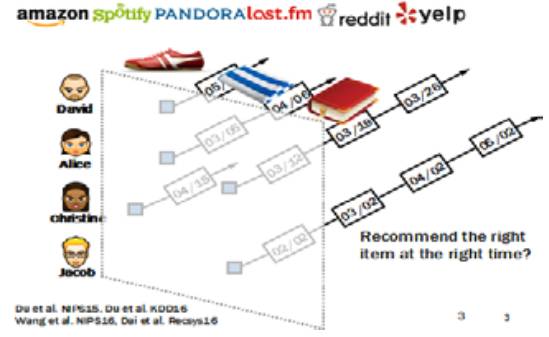
第二个应用是关于推荐系统。
通常情况下,对于推荐系统你会很自然地想到矩阵分解的方法,但是在这里面,我们也可以使用在图上推理的方法,用这种方法解决这个问题。
 第三个问题和知识推理有关系。
第三个问题和知识推理有关系。
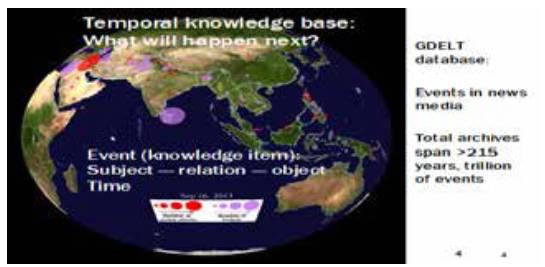
特别地,我会在一个带有时间的知识库上,有一个叫做 GDELT,也就是从实时新闻抽取一些知识,每个抽取知识包括subject(一个关系),还有一个Object以及知识点的时间。知识的图是随时间进行变化的,那怎么在上面进行建模和推理?
 第四个是关于医疗方面的。
第四个是关于医疗方面的。
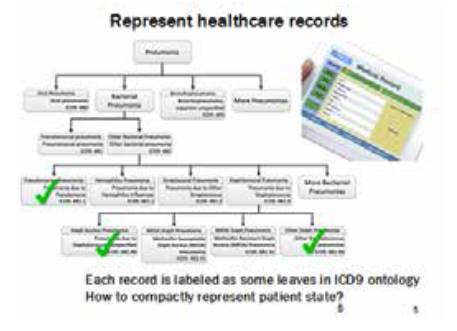
很多情况下现在医疗的records都是记录了一些每次你 去医院的病征,所谓Medical Record,这些病征是通过图联系在一起的,你也希望通过图进行表征向量,进行推理。
我会从第一个开始讲,当然还有很多其他问题,这里不涉及。这都是和图有关的,需要对这些图上的节点和边进行向量表征进行推理。有时图不仅是图,实际上很多 情况下在图上还有一些动态信息。比如, 你有一个社交网络,人并不是一个死的节点的人,会产生很多事件,很多时间上的一些信息。这时我们同时也想对这个图结 合时间上的信息进行建模。我这里要讲的就是一个通用的方法,对图甚至图上的动态信息进行一个向量化的过程。
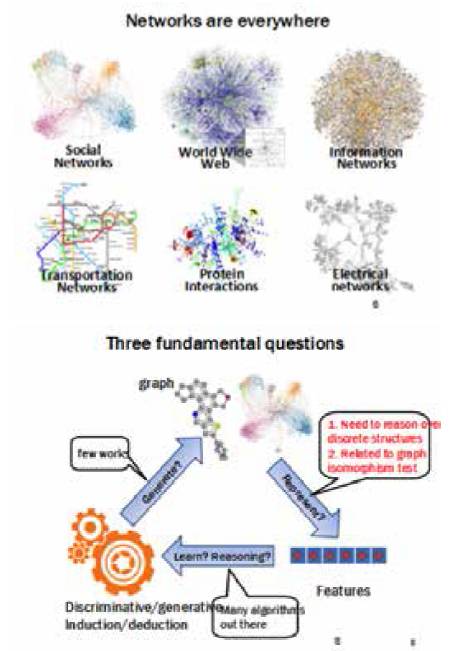
大多数的机器学习方法都是基于向量的数据进行建模和学习的。而图是一种组合优化的离散结构,一开始不容易用那些机器学习的方法来建模。那么,我们首先要解决的问题就是怎么把图这样的离散结构表达成一些向量结构。这和计算机或者 是数学里的一个非常基本的难题有关,就是Graph Isomorphism 的问题——比较两个图是不是不同,有多少不同。
原文链接:
http://mp.weixin.qq.com/s/HiZCb9qdra7XnHcc8_KxJA





