平时见得最多的也许是柱形图了，但我个人最喜欢的却是散点图。在讲散点图之前，我先阐述一个不太严谨的个人观点。我认为，所有的数据图表都可以分为两类，一类是偏重于展示，一类是偏重于研究。如何理解？偏重于展示的图表，往往是将某个指标所蕴含的信息更为直观地表达，即该类图表中获取得的信息，是可以直接应用于业务决策的。比如某公司全国各省的销售员人均销售业绩的柱形图，孰高孰低被展现得很明显，那么哪些地区需要努力，或者哪些地区需要裁员，就可以进行决策了。
偏重于研究的图表，往往是显现出指标间的某些隐藏的关系，从图中得到的信息往往需要进一步的研究，才能落地为具体的业务判断或执行策略。比如某公司人均销售业绩与员工离职率的散点图，你或许能看到两者存在某种数学关系，但你并不能获得显性的结论，而是需要通过进一步的研究，比如回归建模，才能提取出这种关系。
研究型的图表就像一扇门，经常能帮助我们打开另一番天地，获得的信息价值也更高；但相对的，也有更高的风险，许多时候你投入很多时间，获得的结论却没有价值。
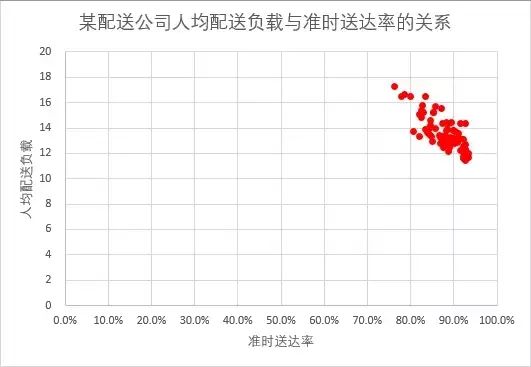
散点图最核心的价值在于发现变量之间的关系，千万不要狭隘地将这个关系理解为线性回归关系。指标间的关系有很多，如线性关系、多项式关系、指数关系、对数关系等等，当然，没有关系也是一种重要的关系。最基本的散点图我们来看一个典型的散点图，下图展示了一家外卖配送公司配送员人均负荷（一天需送掉的订单量）与订单的准时送达率。
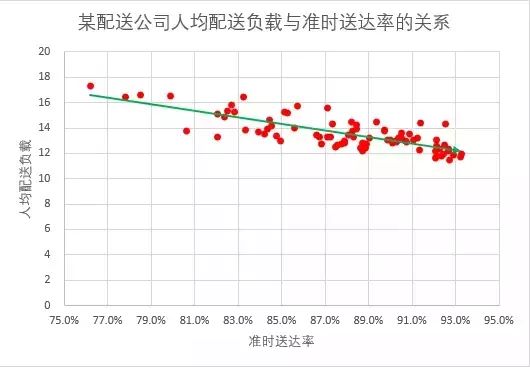
散点图的基本元素就是点，即通过两个变量（纵坐标轴和横坐标轴）的数值，将点打在图表对应的位置上，通过散点的分布，来观察两个变量之间的相互关系。通过上图我们就能直观地看到，人均配送负载和订单的准时送达率是负相关的关系，即人均配送负载越高，准时送达率越低，而人均配送负载越低，则准时送达率越高。我们通过添加一条趋势线，来使得这个关系更为明显。
对于一家外卖配送公司，这个结论似乎是一个常识，当一个人一天要配送的订单越多，则他就越难准时将所有订单送到。其实，这个逻辑未必是成立的，真正的解读是：如果订单是循序渐进，在时间分布上平缓地递交给配送员，那么单再多，配送员能一单单送完，则超时率是依旧平稳地；但实际情况并非如此，外卖配送需求都是在高峰时间段脉冲式增长，这就导致配送压力大时，配送员同时承接了多个订单，这就导致了手头总有一部分订单会因为绕路配送而超时，这才导致了如下散点图上的反映。
其实散点图的制作只需要三部操作：1.点出散点图制作控件；2.选择数据；3.调整图表参数首先点击“插入”选项卡下的“图表”模块，在左边的图表选择项中，选择“XY（散点图）”，暂时先选择第一种类型，后面的几种类型会慢慢介绍。如图2-2，点击“确定”按钮后，就会生成一个空的散点图。如图2-3，右键点击图形，选择“选择数据”，就会出现如图2-4的数据源选择框，在这里点击“编辑”按钮，进入如图2-5显示的“编辑数据序列”界面。在“编辑数据序列”这个界面当中，我们需要设置三个数据，第一个是图标标题，你可以选择某个单元格，会出现对你选中单元格的绝对引用参数；第二个是X轴上要显示的指标，你可以操作鼠标在Excel表中圈选，也可以自己输入绝对引用语句；第三个是Y轴上要显示的指标，方式与第二个相同。
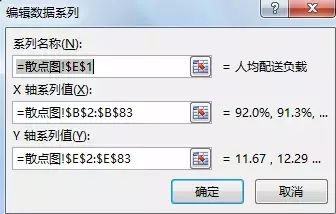
选好数据后，一个最初级的散点图就会展现在你面前了。需要注意的是，最初的这个图往往没有你想象的漂亮，经常你会发现散点集中在某几个较小的区域。如图2-6，不要惊慌，这样的原因往往是你没有调整好横纵坐标轴的“坐标轴选项”。双击坐标轴，将数据展现区间调整好合适的范围。如图2-6，原来的横坐标轴区间是0.0-0.95，但是我们大部分的点集中在0.75-0.95之间，因此我们将横坐标轴区间调整到0.75-0.95，这样图表看上去就美观多了，更重要的数据间的关系也被清晰地呈现出来了。除了对坐标轴缩放的操作，我们还经常会用到“坐标轴选项”里的“单位”和网格线的格式，因为有时我们需要调整坐标轴的颗粒度，以使得散点的位置展示得更为精确。当散点较多且较为细密时，我们需要将网格线调整为虚线并弱化颜色，使得散点间的关系能更为突出。
散点图只表达了两个变量的关系？不是的，我们还可以在点上做文章。可以用点的大小来衡量另一个变量。这样，散点图就变成了气泡图。为什么叫气泡图？答案非常直观，有大有小的圈圈，最像的就是气泡了。且我们在制作气泡图时，往往会设置颜色的透明度，以展示气泡的密集程度。这么一来，气泡图就更直观了~
如图2-8，我们用气泡的大小来表示配送费收入，这样我们就可以观察三个变量之间的关系了。我们看到，无论从人均负载的角度还是准时送达率的角度，配送费都没有呈现出与其他两个指标的相关关系。小结一下，从图2-8中，我们能够获得的认知有如下几条：1. 人均配送负载与准时送达率有明显的负相关关系，即一个指标随着另一个指标的增长而减少。2. 每单的配送费与人均配送负载和准时送达率都没有呈现出明显的相关关系。3. 样本点大部分集中在准时送达率87%-93%，人均负载11-15的区间范围内，说明配送员的一般状态就在这个范围内。
通过以上几点，相信大家以及能领略到散点图的强大了。我们更近一步，给散点图再增加一个变量，即用气泡的颜色来代表另一个变量。需要注意的是，用颜色代表的变量，不适合再用连续型变量了，最好是用类型变量或有序变量。在Excel中，我们不能直接通过导入数据来用颜色来代表某个变量。这是一点小小的遗憾，但我们依然可以手动将效果做出来。
如图2-9，四种气泡的颜色代表了四个配送团队。我们会明显的看到，红色的配送团队的准时率显著领先于其他团队，但在人均配送负载上则比较低，说明红色团队的工作量不是很大，因此效率较高。黑色团队的人均配送负荷较高，准时送达率较低，与红色团队的状况正好相反。蓝色团队的成员则分布非常分散，有的人负载高准时率低，有的人负载低准时率高，可见蓝色团队的管理方式和其他三个团队或许非常的不同，值得进一步的调查分析。
通过从散点图到气泡图的应用，我们不断地窥探出数据指标间的关系，并且挖掘出了许多新的信息，这真的是一个欣喜的发现过程。所以，你们应该能理解为什么我喜欢散点图了吧。
End.
作者：胡晨川（中国统计网特邀认证作者）
关注“数据与算法之美”
获取更多最全数据集
-----这里是数学思维的聚集地------
“超级数学建模”（微信号supermodeling），每天学一点小知识，轻松了解各种思维，做个好玩的理性派。30万数学精英都在关注！
