当我们踏上机器学习的征程时,往往会被一系列复杂而强大的算法所深深吸引。然而,在这庞大的算法海洋中,有一位简单而卓越的"先驱"引领着许多初学者迈出他们奇妙的机器学习之旅——那就是K最近邻算法,简称KNN(k Nearest Neighbors)。这个算法因其直观而易于理解的特性而备受青睐,成为许多学习者迈入机器学习领域的第一步。KNN不仅在分类问题上独具优势,还能轻松应对回归任务,为机器学习课程中的首个算法注入了生机与活力。在我们深入了解KNN的原理和应用之前,让我们先迎接这位"机器学习初探之旅的导师",一同揭开KNN算法的神秘面纱。
什么是k近邻
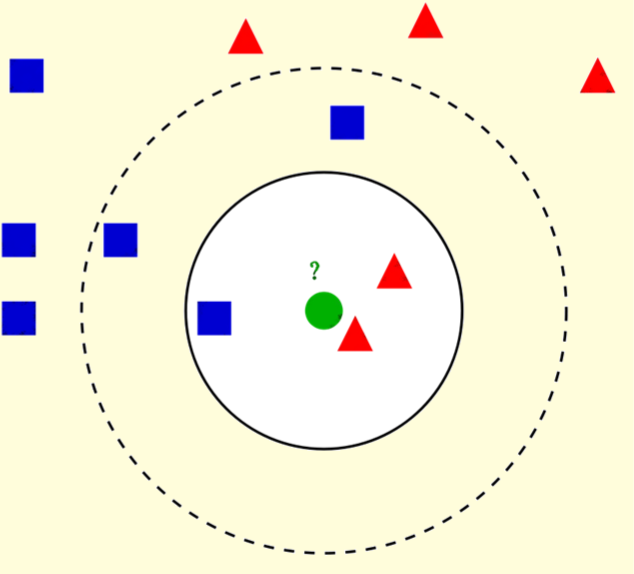
现在,想象一下你有一个新的、未知的样本,你希望知道它属于哪一组。这时,你自然会考虑周围的点。然而,结果实际上取决于你选择观察的范围有多广。如果你只考虑最近的3个点,那么(实心圆)绿点将被归类为红色三角形。但如果你进一步扩大观察范围,那么(虚线圆圈)该点可能会被重新分类为蓝色方块。
这正是k最近邻(kNN)算法的工作原理。根据设定的k值,该算法通过考虑最近的k个邻居中占多数的类别,对新样本进行分类。对于回归任务,算法则是取最近k个邻居的平均值来预测新样本的实际数值。如此简单,就是kNN的魔力所在。
k近邻的特性
k最近邻(kNN)被归类为一种惰性算法
这在机器学习术语中意味着与其他算法相比,它缺乏显著的训练阶段或训练阶段非常短。然而,这种惰性算法的明显缺点在于其预测阶段的速度相对较慢。由于kNN在训练阶段不会明显记住数据,它会在短时间内快速完成训练。然而,预测阶段的速度却相对较慢。在进行预测时,算法需要计算新样本与数据集中每个数据点之间的距离。然后,它会选择k个最小距离,并根据这些邻居的多数投票对新样本进行分类。因此,尽管在训练方面它表现得迅疾,但在生成预测时,kNN会以一种更为谨慎的方式处理数据。
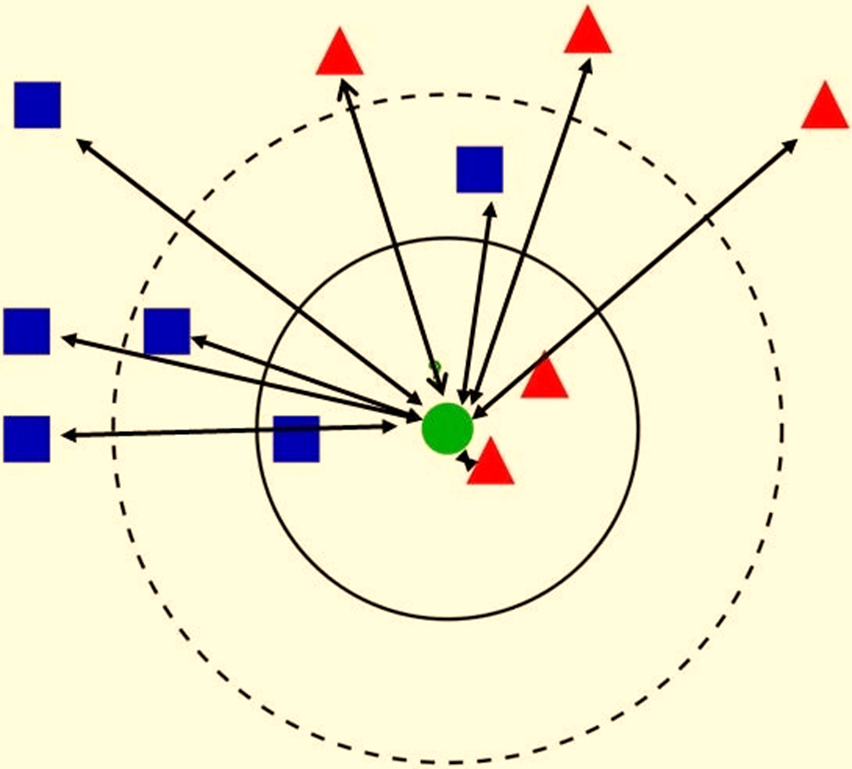
对于人眼来说,标记绿点完全没有问题。但是,如果不计算每个点之间的距离,算法就无法找到最近的邻居。
距离本身是使用 3 个距离度量之一计算的:
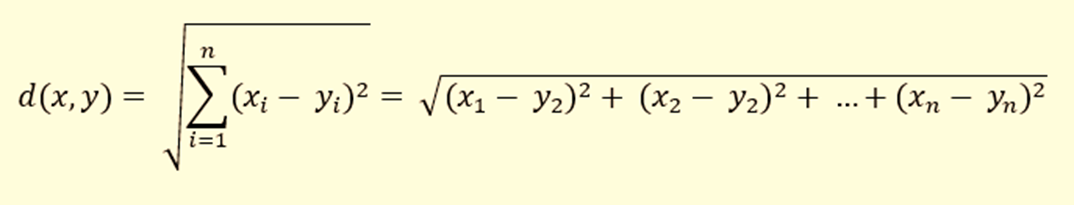
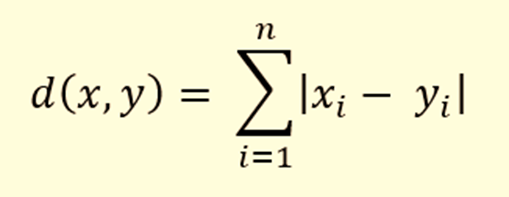
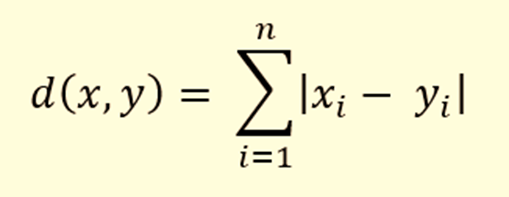
kNN也是一种非参数算法
k最近邻(kNN)也属于非参数算法的范畴,这意味着它对数据的形状和分布没有严格的要求。与假设特征和目标存在线性关系的线性回归不同,kNN不对数据做出这样的假设。正是因为这一特性,kNN被认为是最简单的模型之一,并且在接受适当的数据训练后,其开箱即用的效果非常显著。如何选择k的值
我想您已经意识到,k最近邻算法的结果完全取决于k的值。因此,一个显而易见的问题是:“我们如何选择最佳的k值呢?”不幸的是,这并没有一个明确的答案,因为最佳的k值会随着每个数据集的不同而变化。您的任务是找出能够最大化性能指标(例如准确性)的k值。然而,您可以遵循一些一般的趋势,以在选择k的可能值时做出明智的决策。
首先,选择较小的k值可能会导致过拟合。例如,当k=1时,kNN分类器使用与最近邻居相同的标签来标记新样本,这样的分类器在测试中可能表现不佳。相反,选择较大的k值可能会导致欠拟合,并且会增加计算成本。
重要的是要了解,当您使用不同的k值时,k最近邻(kNN)算法的性能会发生怎样的变化。
在实际应用中,您可以借助诸如GridSearchCV等工具来选择最佳的邻居数量,也可以通过绘制模型复杂度曲线来直观地选择最适合的k值。这样的工具和可视化方法可以帮助您在模型的性能和计算成本之间找到平衡,从而更好地调整k的取值,使其在实际问题中发挥最佳效果。
使用 KNeighborsClassifier 进行分类
对于分类问题,新样本的标签是由最近的k 个邻居中的多数票来识别的。解析来一个示例进行使用kNN进行分类。数据集使用Kaggle 的帕尔默群岛企鹅数据(https://www.kaggle.com/datasets/parulpandey/palmer-archipelago-antarctica-penguin-data)。该数据集包含 3 个企鹅物种的特征:Adélie、Gentoo 和 Chinstrap。我们将利用企鹅的身体测量数据构建一个 kNN 分类器:

import pandas as pd penguins=pd.read_csv("penguins_size.csv").dropna()penguins
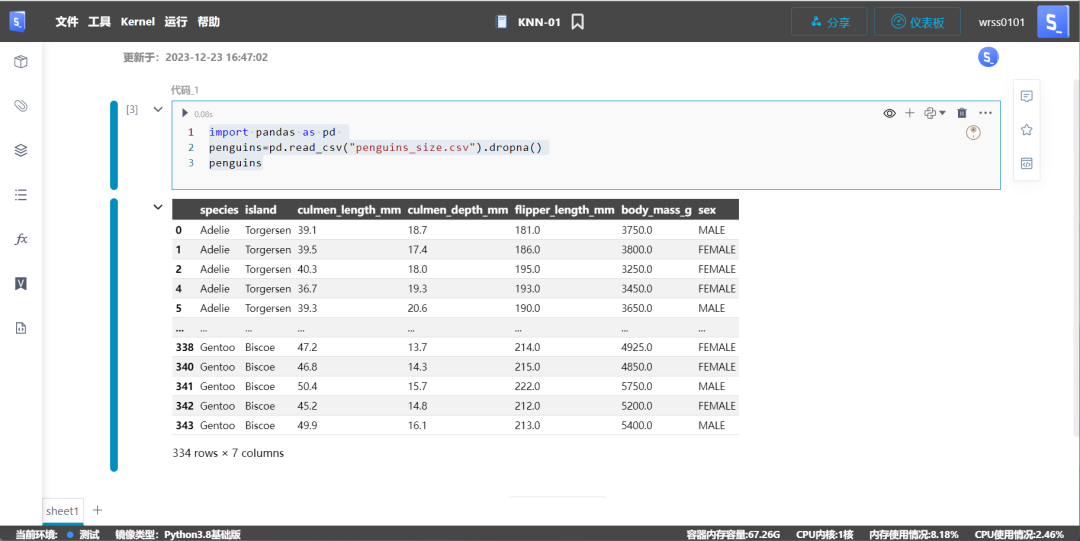
使用 4 列作为特征(culmen_length_mm、culmen_depth_mm、flipper_length_mm、body_mass_g)构建第一个分类器:
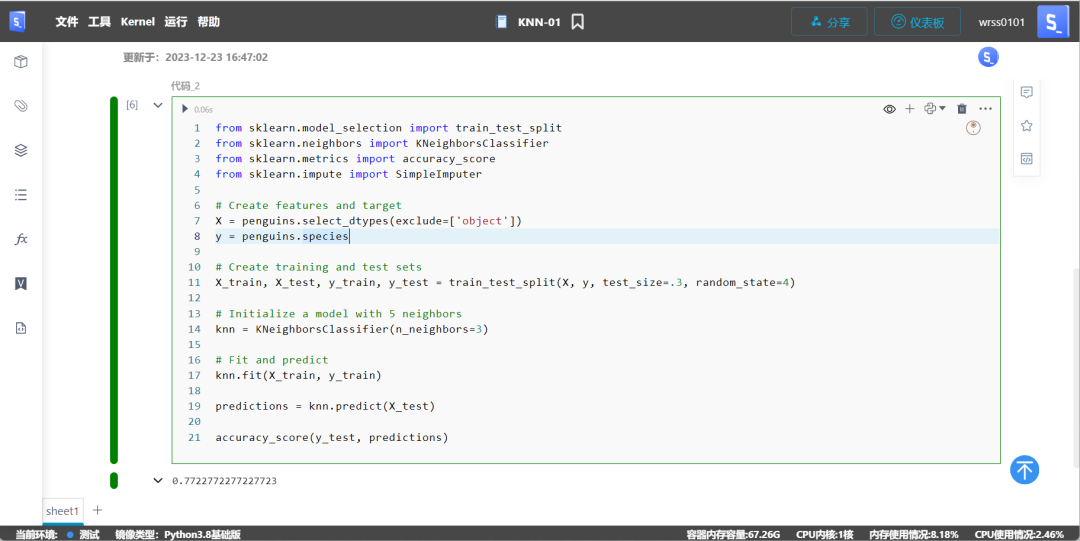
from sklearn.model_selection import train_test_splitfrom sklearn.neighbors import KNeighborsClassifierfrom sklearn.metrics import accuracy_scorefrom sklearn.impute import SimpleImputer
X = penguins.select_dtypes(exclude=['object'])y = penguins.species
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.3, random_state=4)
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)
predictions = knn.predict(X_test)
accuracy_score(y_test, predictions)
模型复杂度曲线(Model Complexity Curves)
尝试不同的k值,并根据它绘制我们的性能指标的结果。一旦你看到它,就会更有意义。函数plot_complexity_curve,它将邻居的可能数字、模型本身和数据作为参数。然后,对于每个k,它在训练集和测试集上对给定模型进行初始化、拟合和评分。在训练集和测试集上对模型进行评分将使您很好地了解哪些值会导致过度拟合和欠拟合:
def plot_complexity_curve(k_list, knn_model, x_train, x_test, y_train, y_test): train_scores = [] test_scores = [] for k in k_list: knn = knn_model(k) knn.fit(x_train, y_train) train_scores.append(knn.score(x_train, y_train)) test_scores.append(knn.score(x_test, y_test))
fig, ax = plt.subplots() ax.plot(k_list, train_scores, label='Training Accuracy', color='red') ax.plot(k_list, test_scores, label='Testing Accuracy', color='black')
ax.set(title='k-NN with Different Values for $k$', xlabel='Number of Neighbors', ylabel='Accuracy') ax.legend()
以上函数重复不同k值进行预测,计算准确度。
import matplotlib.pyplot as pltneighbors = np.arange(1, 15)
X = penguins.select_dtypes(exclude=['object'])y = penguins.species
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.3, random_state=4)
plot_complexity_curve(neighbors, KNeighborsClassifier, X_train, X_test, y_train, y_test)
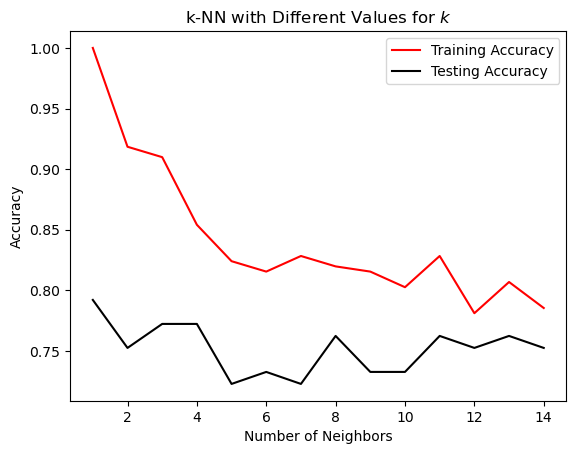
从图中,我们可以看到 3 或 4 个邻居是过度拟合(非常高的训练分数和低测试分数)和欠拟合(训练和测试分数都很低)之间的甜蜜中间点。
特征标准化(Feature Scaling)提升kNN性能
kNN 是一个非常挑剔的算法。它需要一定的数据质量才能正常工作。kNN 的第一个要求是数值特征应该具有相同的尺度。如果您注意的话,身体质量指数栏的比例与所有其他身体测量值有很大不同。一般来说,所有特征都应该进行缩放,使其范围在 0 到 1 之间。MinMax 缩放(称为标准化)的方法来完成。对于分布中的每个数据点,它减去最小值并除以 (max-min):
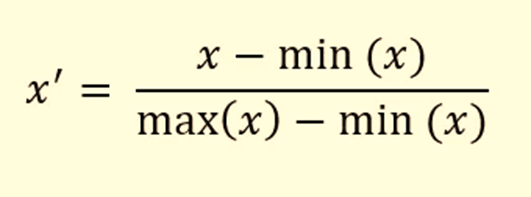
接下来进行数据标准化后进行输出模型复杂度曲线:
from sklearn.preprocessing import MinMaxScaler
X = penguins.select_dtypes(exclude=['object'])y = penguins.species
scaler = MinMaxScaler()
X_prepped = scaler.fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X_prepped, y, test_size=.3, random_state=4)
k_list = np.arange(1, 15)
plot_complexity_curve(k_list, KNeighborsClassifier, X_train, X_test, y_train, y_test)
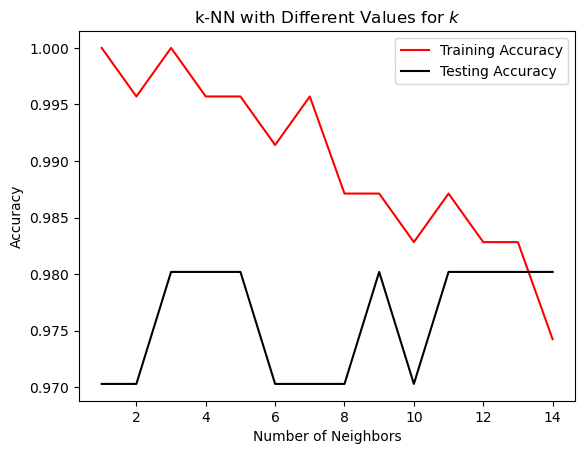
现在所有分数都高于95%了。看看特征缩放对性能的提升有多大。从图中可以看出,保持欠拟合和过拟合之间平衡的k值为 12 或 13。
kNN 的优缺点:
- 直观简单: 算法非常简单,易于理解和解释,使其成为机器学习入门的理想选择。
- 快速训练: 训练阶段通常很快,因为它仅仅是将数据存储起来,而没有显式的学习过程。
- 多功能: 可以用于回归和分类问题,为不同类型的任务提供了灵活性。
缺点:
预测慢: 在预测阶段,由于需要计算新样本与所有训练数据点的距离,速度相对较慢。
内存占用大: 由于存储了所有训练数据点,对内存的使用较大,尤其是对于大型数据集。
大小敏感: 对特征的尺度敏感,因此需要进行特征缩放以避免某些特征对距离计算的主导影响。
对异常值敏感: 容易受到异常值和噪声的影响,可能导致不稳定的预测结果。
维度诅咒: 随着数据维度的增加,计算距离变得更为复杂,这被称为维度诅咒,可能导致性能下降。
K最近邻(kNN)算法以其简单直观、易于理解的特性成为机器学习入门的理想选择。它在分类和回归任务上表现出色,但预测阶段相对较慢,对内存占用大,对特征尺度敏感,容易受异常值干扰,且在高维度数据上可能受到维度诅咒的影响。通过特征缩放可提升性能,选择适当的k值至关重要。在实际应用中,kNN展示了其多功能性和易用性。

















