
上周,有一位粉丝在柴柴的一条微博下面问了这么一个问题。
看完这个问题之后,柴柴脑海中马上浮现出一只乌龟的身影。
那就是被称为“物理学四大神兽”之一的“
芝诺的乌龟
”。

公元前五世纪(中国的春秋战国时期),希腊哲学家芝诺提出了一系列哲学问题,人们称其为“
芝诺悖论
”。
而“
芝诺的乌龟
”就是其中最出名的三个悖论之一。
这个悖论的内容是酱紫滴:
假如阿基里斯和乌龟一起赛跑。
阿基里斯
身为希腊神话中的英雄(特洛伊战争中的希腊将领),不仅骁勇善战,而且奔跑速度极快。

希腊神话中,在阿基里斯还是婴儿的时候,他娘将他带到了冥河,提溜着他的后脚跟把他泡进冥河水里。这让他的身体除了没被泡到的后脚跟之外,其他的地方都刀枪不入,但最后阿基里斯还是在战争中被毒箭射中后脚跟挂掉了。在英语中,跟腱就叫阿基里斯(Achilles)。
那么阿基里斯跑得有多快呢?我们假设他的速度是乌龟的十倍(好像也不是很快?)。
在比赛中,阿基里斯让乌龟开始领先100米,然后奋起直追。
阿基里斯会先跑完开始的100米,但乌龟在这段时间里也向前跑了10米。
当阿基里斯跑完这10米时,乌龟同时又向前跑了1米。
当阿基里斯跑完这1米时,…………
……………………

也就是说,每一次阿基里斯跑到乌龟之前所在位置的时候,乌龟都已经又向前跑了一小段距离了。
所以,阿基里斯永远也追不上这只乌龟。

“芝诺悖论”中还有和乌龟类似的悖论。
二分法悖论
假如一个人要前往一个1公里外的地方。
他会先走完一半的路程。
然后走完剩下一半路程的一半。
再走完一半的一半的一半……
………………

所以,这个人永远到不了目的地。

飞矢不动
一支在空中飞行的箭,在每一个瞬间都会占据空间内的一个特定位置。
它既不会移动到别的位置(因为时间还没流逝到),也不会移动到已经在的位置(因为它已经在那了)。
也就是说这支箭在这一瞬间没有移动,它是在空间中静止的。
而时间是由一个个瞬间组成,也就是说箭其实是静止在每一个瞬间。
换句话说,这支箭没有在移动。

当时的人们意识到这仨悖论绝壁有问题,但又说不清它们到底错在哪里。
特别是前两个……
按照人们的常识,阿基里斯最终一定会追上乌龟,路人最终也一定会到达目的地。
但按照芝诺的描述,这两个过程显然都可以划分成了无穷多份,
那么无穷的过程怎么会有完成的一刻呢?
亚里士多德
最先发现了问题所在,他在自己的书中驳斥道:
虽然通过了无穷多段路程,但通过每段路程的时间也是随着路程变短而变短的
。
于是问题就变成了:
无穷多个大于零的数相加,结果为什么不是无穷大?
过了100多年,
阿基米德
(撬地球那个)发现了一种方法,可以把无穷多个大于零的数的求和得到一个有限值。

最大的黑色快是整个正方形面积的1/4,第二大的黑色块是整个正方形面积的1/4²……白色、灰色同理,而三种颜色加起来等于大正方形面积,所以我们可以得到以下结论:
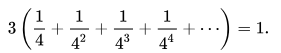
而直到芝诺悖论出现了两千年之后,微积分出现了。

现代微积分被认为是在17世纪由牛顿和莱布尼茨提出,但直到19世纪才发展完善。
不得不说,只要看看大学里
每年
的挂科人数,我们就会发现微积分真的“很能打”。
它确实可以给这类涉及无限过程的问题一个数学上的解释。
所以,现在经常会有人这么说:
“芝诺的龟早已死在了牛顿和莱布尼茨的微积分手里了。”
真的是这样么?我们是否已经真正解决“芝诺悖论”了呢?
也许并没有……
让我们来重新认识一下“芝诺悖论”的提出者~

芝诺,希腊哲学家,亚里士多德称其为“辩证法”的发明者
注意~芝诺是一位哲学家……
“芝诺悖论”也并不仅仅是一个数学问题。
从某种程度上讲,“芝诺悖论”所陈述的问题非常简洁。
而“非常简洁”同时也意味着“非常模糊”。
因此,芝诺悖论就像是
罗夏测试
中的墨迹一样。
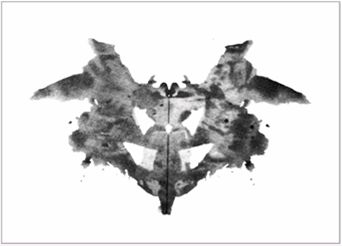
罗夏测试:参与者在观察10张类似于上图的墨迹后,回答这些墨迹看起来像什么,
由于墨迹的形象“非常模糊”,不同的人看完之后给出的答案也各不相同。人们会以此来
评估参与者在动机,反应,认知,情感方面的心理倾向。
同样一个问题,有些人听完会去思考“
阿基里斯到底能不能追上乌龟?
”
就跟我们之前说的那样,这是一个数学问题,已经被现代数学彻底解决了。
还有一些人听完会去思考一些更深层次的问题:
比如
时间、空间、和运动的本质


















