
文 | 黑爪
昨天到今天,估计不少同学都想起了概率课里讲到正态分布、二项分布时的一个经典应用:航班超额订票(overbooking)。MIT/ICAT(MIT国际航空运输中心,International Center for Air Transportation)的一名研究工程师将这种超售模式称为“收益管理的黑暗艺术”,因为迄今为止,航空公司利用数学魔法得出的超售额还并不能保证它永不出错。
我相信大部分人都知道我说的是什么事,但简单回顾下事件经过无妨:4月9日周日晚,芝加哥奥黑尔机场,美联航3411航班因超售导致座位不够,希望征得一名自愿者放弃本次航班,以400美元现金和一晚住宿作为赔偿,并改乘次日(周一)航班旅行。在无人自愿放弃的情况下,航空公司让所有旅客登机。而登机后的情况,则由只需1名自愿者放弃座位,升至4名。在仍无人自愿放弃的情况下,美联航工作人员隧随机抽取,之后动用保安采用强制手段,迫使一名旅客下飞机。引爆舆论。
按照维基辞典的定义:超额预售或预订,是在销售波动较大的商品或服务过程中,出售超过实际容量或产能的行为。
这在运输和酒店行业是惯例,其目的是降低由旅客取消预约(no-show)产生闲置座位而带来的收益损失。
因为联程航班前半段延误,或者其他种种原因,通常总会有旅客没有如期出现的情况。假设航空公司通过一名旅客获得的收入,只有在他/她实际乘坐了这趟航班时才产生,这种情况下,很简单每一个空座都是损失掉的收入。在明知会有旅客不能如期出现,航空公司通过多出售一定数量的机票,并希望到时出现恰恰装满一飞机的旅客数。对于一个在21世纪的头10年间损失高达600亿美元的行业,扭亏为盈比什么都重要。起飞时的空座只意味着一件事:收益损失。而飞机座位是有保质期的商品,就像水果,舱门关闭那一刻,座位也就过期了。于是就有了超售,这一航空公司希望最大化每一趟航班收益所采取的措施。
然而超售的风险也是显而易见的,并且时有发生,那就是出现的旅客数超过预期,飞机上没有足够的座位。这直接导致了本文所讨论热点事件的爆发。
因此
超售的比例就变得至关重要。使其既要最小化损失,又要最大可能地避免上述情形的发生。不单重要,这么多年下来,尽管这个应用案例都进入大学研究院概率课的教科书,人们利用各种概率模型,希望获得最安全的超售比例,然而既然是概率事件,概率再小也有发生的可能。
据2004年的统计数据显示美国航空业的爽约客比例一度高达15%—20%,在加重了爽约罚金之后,这个比例有所降低,但仍然高达10%—15%,
若无超额预订所带来的弥补,空座10%—15%要是发生在旅游旺季,航空公司的心理阴影面积真是很难估量。
然而有效的超额预订能带来的收入增量,却几乎等效于全价票的作用。这意味着,用大概率的收入增量,去弥补小概率的“拒绝登机”赔偿。从总量上看,超售肯定是赚的,赔偿损失对于超售带来的收益增加,只是极小的比例。因而航空公司的收益管理,基本上是围绕着超售模型在进行。企业关心收益是它的本分,这与关心顾客利益不冲突,只有满足了顾客的利益,它才会有长效稳定的收益。
来具体看一下决定超售机制的原理,先解决几个术语:
· CAP:物理容量,即实际可容纳旅客数,也就是实际座位数。
· AU:授权容量,可预售票数。
· BKD:已确认的预订数,它显然 <= AU。
· GS:提早到了机场,并希望搭乘去往同一目的地的更早航班的旅客。若更早航班有空座,这类旅客便可以按候补旅客(SB)的状态搭乘早班;否则超常搭乘其预订航班正常旅行。这类旅客被称作Go-show。
· SB:候补旅客,在没有预订特定航班的情况下,而希望搭乘该航班的旅客,被称作Stand-by。通常有两种情况,一是错过了预订航班,希望改乘下一班的旅客;二是前面一条所定义的早到GS旅客。
· NS:未如期出现并办理登记的旅客,被称为No-shows。
· SU:如期出现并办理登记的旅客,被称为Show-ups。
· NSR:未出现旅客率,no-show率。
· SUR:出现旅客率。
· PAX:登机旅客数。
· DB:被拒绝登机。
· SP:空置数。
以上变量在超售机制中存在如下关系:
1.PAX = min [ BKD - NS + GS + SB, CAP]。
登机的旅客数 =(已确认预订的旅客数 - 未出现旅客数 + 早到旅客数 + 候补旅客数,座位数)这二者中的最小量
= BKD + GS - NS + SB - DB
=确认预订旅客数 + 早到旅客数 - 未出现旅客数 + 候补旅客 - 被拒绝登机
2. BKD = NS + SU
确认预订的旅客数=未出现旅客数 + 出现旅客数
3. SU = PAX + DB - GS - SB
出现旅客数=登机旅客数 + 被拒登机数 - 早到旅客数 - 候补旅客
4. NSR = (BKD - SU) / BKD
未出现旅客率=(确认预订的旅客总数 - 出现旅客数)/确认预订的旅客总数
5. SUR = SU / BKD = 1.0 - NSR
出现旅客率=出现数/确认预订总数=1.0 - 未出现旅客率
6. SP = CAP - PAX
空置数=物理容量 - 登机旅客
这样,超售率,也就是OV> 1.00,从而 AU = CAP * OV,即可售票数=实际座位数*超售率。建立起一个合理超售机制的数学模型,难点显然在于,不出现旅客率存在着极大的不确定性。
按照MIT/ICAT(MIT国际航空运输中心,International Center for Air Transportation)的相关课程的讲解,民航业在发展过程中,经历过如下几个阶段的超售机制进化:
第一阶段,依赖人工判断来设定超售率。
它基于市场经验和最近期的no-show历史数据,倾向于选择 OV = 1+NSR (no-show率,或更低),倾向于避免出现DB(拒绝登机),显然稳妥而保守,但没有达到收益最大化的效果。
例如,CAP=100,平均 NSR=.20,那么:AU = 100 (1.20) = 120,可售120张票。
第二个阶段是基于近期历史数据,对于平均NSR进行估值。
假设BKD=AU(最坏的情况:确认旅客数=可售票数),求AU,以使得 AU - NSR*AU = CAP,也就是说,卖出去的票减去没出现的旅客数,恰恰等于实际座位数。或者,使得AU = CAP/(1-NSR),即,售票数=实际座位数/旅客出现率。
例如CAP=100 而 NSR=0.20, 那么 AU = 100/(1-.20) = 125
第三个阶段是概率/风险模型
,将NSR(no-show率)的不确定性纳入考虑:历史NSR的标准差STD。若默认NSR(no-show率)呈正态分布(就是常说的钟形曲线),求AU可售票数,使得DB=0,即,不会出现拒绝登机的情形。假设BKD=AU(确认订票旅客=可售票数),置信水平为95%,当BKD=AU(确认订票旅客=可售票数)时,使出现的旅客数少于或等于实际座位数,求SUR*(出现率SUR的均值),以使得 AU x SUR* = CAP(可售票数 x 出现率均值 = 实际座位数),且(可售票数 x 出现率均值”)大于 实际座位数的概率为5%(即:Prob[AU x SUR* > CAP] = 5%),按照正态分布,SUR* 将满足:Z = 1.645 = (SUR* - SUR)/STD
在给定CAP(实际座位数),SUR(旅客出现率),STD(标准差)的情况下,在95%的置信水平上,使DB=0(拒绝登机数为零)的最优AU(售票数):
AU = CAP /(SUR + 1.645 STD)
例如当标准差STD= 0.05时,AU = 100 / (1-0.20 + 1.645*0.05) = 113
标准差STD越大,分母越大,最优的售票数AU就越低,因为这时旅客不出现( no-shows)的风险/不确定性也越高。
在这个机制的基础上,航空公司可以通过以下几种方式来调整售票数:
1. 降低超过DB(拒绝登机)限制的置信水平,这样分母中的Z降低(上例中的1.645),可导致售票数AU的增加。
2. 寄望于自愿DB(VOLDB),来增加DB容忍度。这时上述公式里的分子变为 (CAP+ VOLDB),这也可导致售票数AU的增加。
第四个阶段是基于成本的超售模型。
这个模型里的售票数AU,需要最小化如下两个组成部分的成本:拒绝登机DB的成本 + 闲置SP成本
对于任何一个给定的售票数AU:
总成本 = $DB * E[DB] + $SP * E[SP]
其中,$DB和$SP分别为:每一个拒绝登机和每一个闲置座位的成本;E[DB] 为给定售票数AU 条件下,预期的拒绝登机数DBs;E[SP]为给定售票数AU 条件下,预期的闲置座位数SP。
这时的超售模型,便是在售票数AU的一个范围内,建立的一个数学模型用以寻找使得总成本最小的AU值。
用两张图来说明:
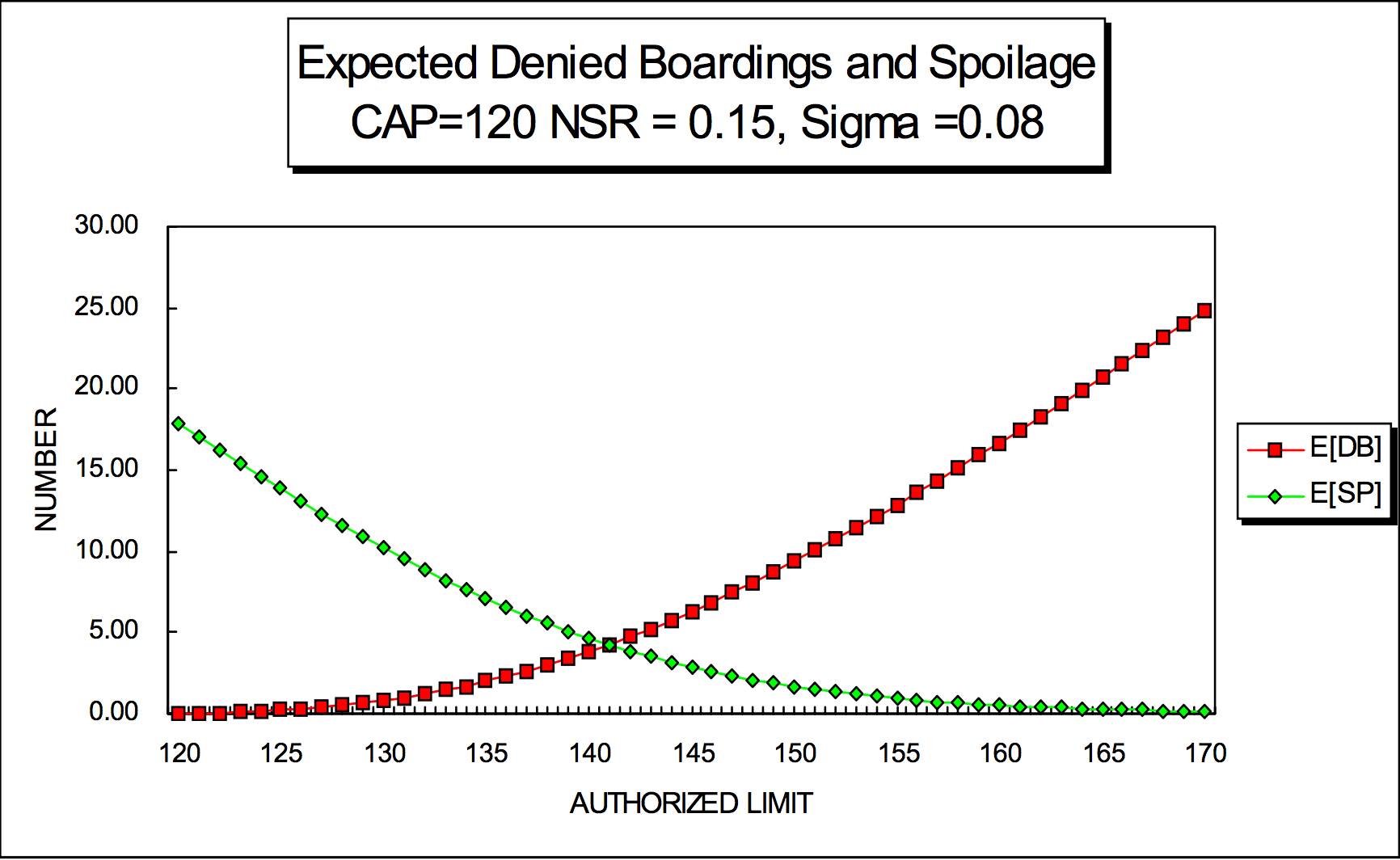
预期DB数和预期SP数关系图:横轴表示售票数;纵轴为指标衡量:绿色值代表预期闲置座位,红色值代表预期拒绝登机数。给定实际座位数120,no-show率0.15,标准差0.08。(图片来源:MIT/ICAT讲义)
这里其实便是一个有趣的优化问题。这120个座位,若航空公司出售120张机票,预期拒登机E[DB]为零,而预期闲置座位数E[SP]则最大,18左右。而如果航空公司出170张机票(如图),飞机倒是坐满了,但预期拒登机E[DB]则高达25个左右,发放免费旅行券和延误旅客的食宿开销又将引起收益降低,且不提商誉损失。所以,关键便在于找到那个让收益最大化的完美点,本图中的两条曲线在预售数为141左右相遇。
从成本角度,它说明了什么呢?
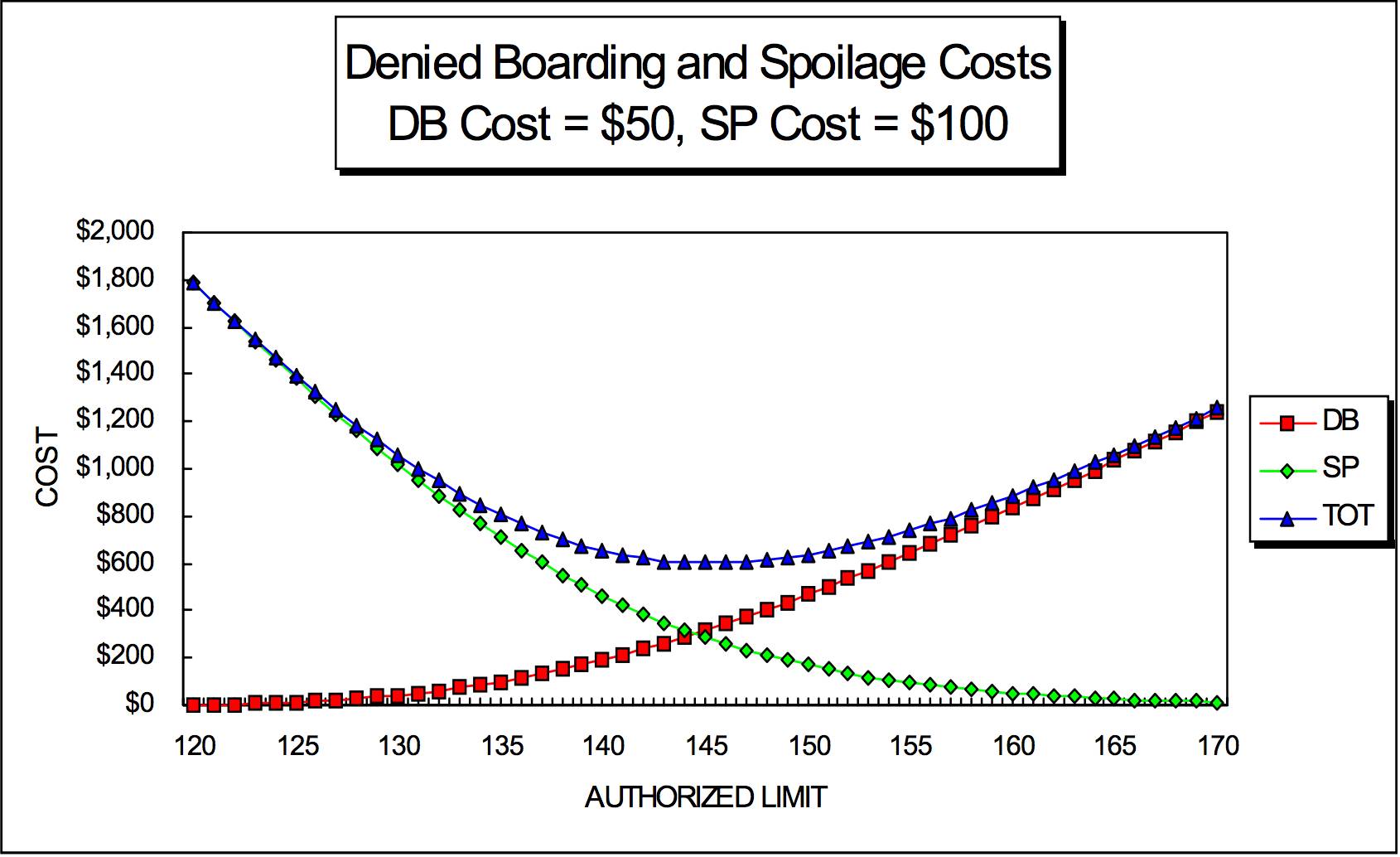
拒登成本和闲置成本关系图:该图横轴表示预售票数;纵轴为成本:绿色值代表闲置成本,红色值代表拒绝登机成本,蓝色代表总成本。给定单个拒绝登机成本为50美元,单个闲置成本为100美元。(图片来源:MIT/ICAT讲义)
图上显示,总成本在预售数为140到145这个区间时最低。
拒绝登机的成本究竟包含了哪些项目:
- 非志愿DB的现金赔偿;
- 志愿DB的免费旅行代金券;
- 未能如期飞行旅客的餐饮、住宿;
- 其他航空公司的座位;
- 商誉成本。
然而遗憾的是,成本所包含的项目虽然界定清晰,然后为模型提供准确的DB成本作为输入,却很多航空公司都没有很容易做到。
再来看,座位闲置成本,它表面上看上去非常简单,就是飞行航班里空座位原本可以有的收入。
但是怎样来计量这些损失的收入却同样不易:是采取该程的平均票价?还是因为停止预售以后,失去的往往是临时订机票,也就是高价位票的旅客,所以应该选用该程的最高票价?或者,因为高预售数意味着允许更多的特价票,而应该选用该程的最低票价?
从服务和商誉的角度,很多航空公司倾向于把大胆的超售视为负面影响,因为拒绝登机,无疑总是与低质量的服务和丧失商誉联系在一起的。然而问题在于,闲置座位带来的收入损失,可能比DB成本更高。
因而如何完善邀请自愿DB的方案,其实成为关键。也就是说,航空公司究竟应该对“自愿拒登”的旅客有多好?一个完善的自愿DB方案,需要训练有素的地勤人员,他们能够高效地在check-in环节甄别出可能的自愿乘客,并为之提供尽可能多的“软性”赔偿,以使乘客愉快满意。美国的航空公司过去从总体上来说,在处理拒绝登机的问题算是比较成功的,据一份较早(2004年)的统计,95%的DB均为自愿。但近年来寻求自愿者越来越难。
“善待自愿者,是制造商誉的良机。”这是MIT/ICAT(MIT国际航空运输中心)超售课程讲义的结语。从经济利益上讲,通过前面的分析可以看出,这不难。
与本周日事件中那位不幸的乘客一样,《纽约时报》2010年报道过一位叫蒂凡尼·塞姆林的女士的遭遇,她从加州弗雷斯诺出发,搭乘达美航空的航班在盐湖城转机,前往休斯敦参加她祖母的葬礼,不幸在盐湖城转机时被“非自愿拒绝登机”。航空公司给予她400美元的现金赔偿,以及次日的航班,但这就意味着她将错过葬礼。最终萨姆林女士辗转周折如期参加了仪式,但是并非航空公司主动为她提出的解决方案。

▲
讽刺漫画:什么意思,本次航班超售?我是机长。(作者供图)
航空公司在处理拒绝登机这个问题上是否平等,大概是争议最多也最受瞩目的焦点,答案自然是不平等:商务舱旅客和常旅客比其他人遭遇拒绝登机的可能性小很多。最可能被“非自愿拒登”的,是持打折票的观光客。另外,据说网络check-in似乎能减少你被“非自愿拒登”的机会。族裔肤色的说法很难令我信服,一个要去参加祖母葬礼的白人女子如何也被选中了呢?
本文原标题《
航空公司该对“自愿拒登”的旅客多好才叫好?
》
·END·
大家
∣
思想流经之地
微信ID:ipress
洞见 · 价值 · 美感

※本微信号内容均为腾讯《大家》独家稿件,未经授权转载将追究法律责任,版权合作请联系
[email protected]





