提到贝叶斯推断，就不得不提Bayesian Methods for Hackers 这本书，简单易懂，印刷精美。犹记得当年第一次见到ipython notebook 就是因为这本书就是用notebook写的，现在也有了中文版。中文版翻译的水平很高，当我拿着这本书的中文版准备跟大家分享时，看到第一章标题 “贝叶斯推断的哲学” 这句话时，我邪恶了一下。脑子里迅速闪过更衣室大战的哲♂学六边形
哲♂学六边形
我本来是想用 哲♂学 来讲解贝叶斯思想的，但是由于现在的时代主题是反♂腐，所以我还是以反腐为例子，以《人民的名义》，谈谈贝叶斯思想吧。
赵处长是人民公仆的概率
谈反腐之前，先介绍一下贝叶斯学派的哲学和经典学派有什么区别。书中给了一个这样的解释：经典统计学家眼中的概率，实际上是一连串长期发生的事件的频率，比如坐飞机失事的概率是多大？经典统计学家的套路是，找出近几年全球航班的飞行次数，作为分母。再找出对应时间范围内航班的失事次数，作为分子。于是失事的概率就是：
场景1：第一张搜查令
在跟着剧情，感受贝叶斯推断的哲学之前，我们得蒙一个先验概率。先验概率重要吗？其实比较重要，但不起决定性作用，所以可以蒙一个，只要不离谱。蒙多少呢？这一开始一帮检察官就去“社区送温暖”，应该不会冤枉他吧，八成有问题，那就蒙 20% 可能性是人民公仆吧。
社区送温暖得出0.2的先验概率
但是继续看下去，似乎不对，哎，这个赵处长，是腐败分子的话，怎么吃这么差，住这么破，而且住处最后搜半天啥都没有？人民公仆候处长活的也比他强啊！
来，我们把刚才的想法，用贝叶斯公式写一下。假如说，我去中纪委，翻了近几年腐败分子的所有卷宗，总结出腐败分子平时吃的如何、住的怎样，家里有没有问题，应该可以得出这样的一种分布
P(D|θ),θ=人民公仆or腐败分子" style="display: inline; line-height: normal; font-size: 20px; text-indent: 0px; letter-spacing: normal; word-spacing: normal; word-wrap: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border-width: 0px; border-style: initial; border-color: initial;">P(D|θ),θ=人民公仆or腐败分子P(D|θ),θ=人民公仆or腐败分子：
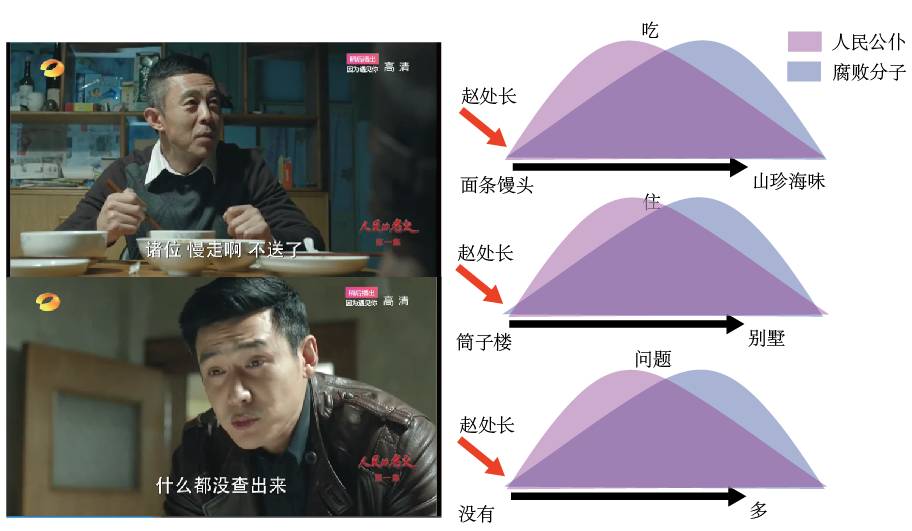同一剧情，腐败分子和人民公仆的不同可能性
什么？人民公仆也山珍海味？家里也一堆问题？忽略这个，只是举个例子而已，美术不好画不好那种曲线，哈哈，大家别举报我。假如啊，从我在中纪委的资料统计结果来看，可能只有 1% 的腐败分子吃的小于等于赵处长，而有 20% 的人民公仆吃的小于等于赵处长，再基于我们之前社区送温暖应该有问题、P(θ)=0.2" style="display: inline; line-height: normal; font-size: 20px; text-indent: 0px; letter-spacing: normal; word-spacing: normal; word-wrap: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border-width: 0px; border-style: initial; border-color: initial;">P(θ)=0.2P(θ)=0.2的先验概率，求第一张搜查令的剧情的概率：
提示：
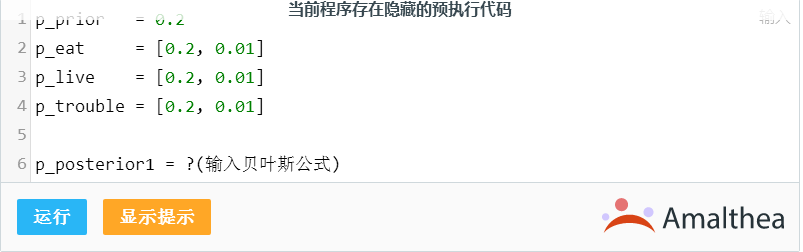
证据面前，我们发现，与先验概率不同的是，这很可能是个人民公仆啊！
场景2：第二张搜查令
没搜出啥，看起来候处长走了，到楼底下，亮出第二张搜查令，去搜赵处长办公室。搜出了些私房钱，半瓶五粮液，确实有点寒掺，都不如人民公仆。赵处长觉得火候到了，跟检察机关拍桌子瞪眼，结果检察机关果断亮出证据，你肯定有问题，我们没办过错案，然后赵处长忙中出错的交代了被人行贿的事实。
好了，我又去中纪委翻资料了，给出了这几个事件的概率：
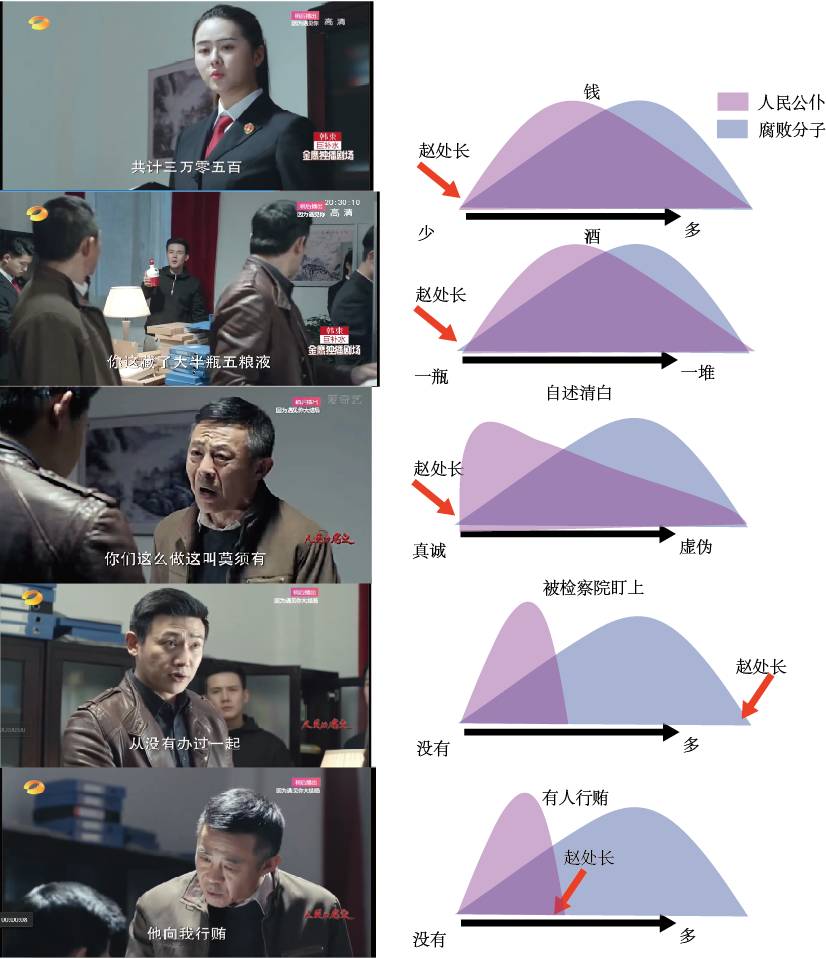同一剧情，腐败分子和人民公仆的不同可能性
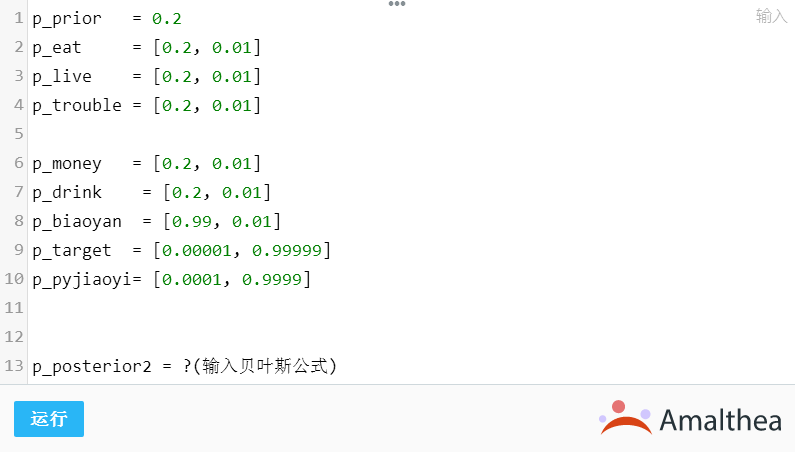
OK，结果显示，这人已经不像是个人民公仆了。原因很简单，我们相信被候处长盯上的人这么多年来都是腐败分子，除非是中了彩票(经过统计发现这种人通常 99.9% 有问题)。但是这也只是感觉而已，正如赵处长所言：
场景3：第三张搜查令
这个不用我仔细写了，我不用 0/1 表示，并非漠视法律，而只是为了防止无法计算而已。
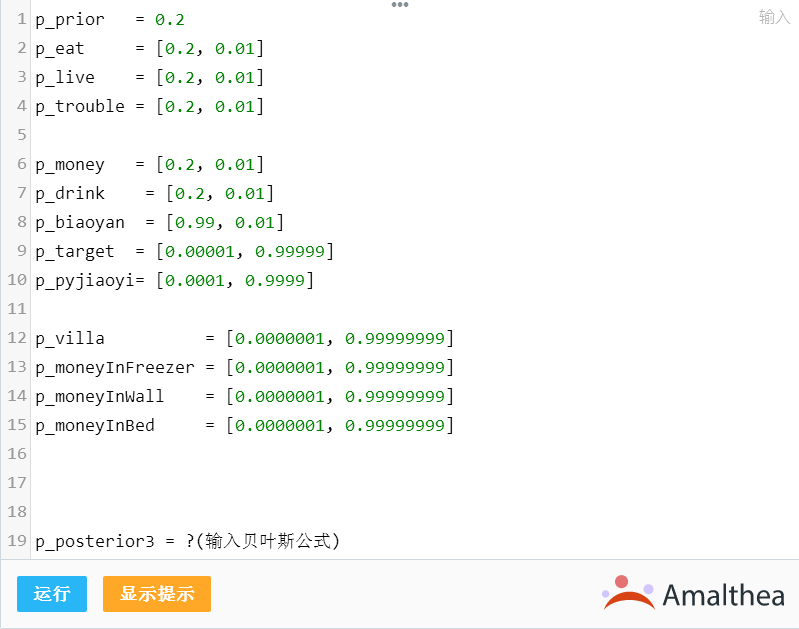
结果显示，是人民公仆的概率还有那么百分之几，就当是给他这么多年来辛苦表演的回报吧，确实，从这个角度上来说，他演的确实很像一个人民公仆。当然这个只是贝叶斯的哲♂学，不是法律的规定。我们这里把赵处长前面各种表演成分加进去，只是为了娱乐，法律决不允许腐败分子用演技逃脱罪责。
跟着贝叶斯的哲学，感受剧情的高潮迭起
综上，我们选用了这些关键剧情，构成了赵处长在前两集中，是如何先被怀疑，然后通过表演企图逃脱法律惩处，最后在铁一般的事实面前低头认罪。这一系列过程中，随着剧情发展，贝叶斯模型基于的数据也不断变化，导致贝叶斯先验分布经过数据估计得到的后验分布，也是随着剧情不断发展而跌宕起伏的变化的。这一过程如下：
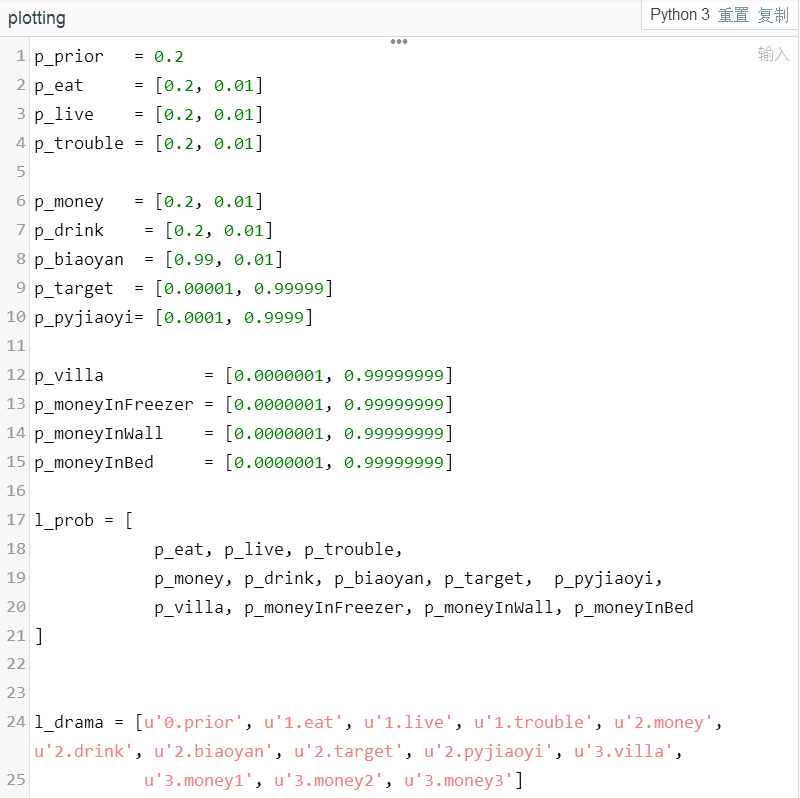
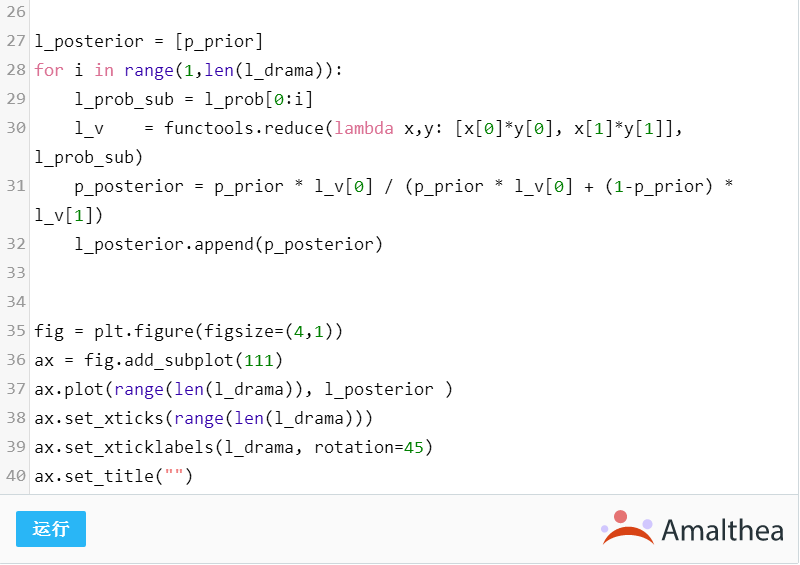
是的，根据贝叶斯的哲学，基于剧情分析的话，对赵处长进行的一系列搜查过程中，他的清白指数一直非常高，但是也并非完全没有问题，毕竟以往也有腐败分子这么清白。赵处长为了彻底坐实自己的清白，发挥了他的表演天赋，拍桌子瞪眼要去请律师，企图完全坐实自己是人民公仆的这个事实。他的目的也几乎达到了，他的真诚与愤怒让我们几乎都要相信他是个人民公仆了，直到猴子一句“我干了快二十年了，从没有办过一起冤假错案”，给了腐败分子当头棒喝，其清白指数直线下降，赵处长在这一过程中自乱阵脚，交代了被人行贿的事实，最终在第三场搜查中，彻底现行。
写在最后
这篇文章其实是我的深度学习系列文章的一个前传。贝叶斯推断对深度学习而言，至少是在调参的这一环节，是十分有用的，比如神经网络的框架定下来以后，具体每一层的参数怎么设定会得到最好的结果？比如卷积核大小、数量等，这些都是深度学习过程中不会被模型自动优化的、需要手动指定的参数，即超参数。
那么能不能再套一层，优化超参数呢？一篇非常经典的kaggle 冠军作品分享Kaggle大赛：债务违约预测冠军作品解析提到了四种超参数优化方式：网格搜索、随机搜索、基于梯度的优化以及贝叶斯优化，并且贝叶斯优化得到了最佳的结果。因此，这篇文章的主要目的，就是介绍贝叶斯参数估计与统计推断相关的基本知识。
媒体合作请联系：
邮箱：[email protected]
