把数学题变成
一顿饭
今天小天又双叒叕给超模君分享了一道题目。
上次超模君就是因为“求阴影面积”，被小天这个家伙套路了一顿饭。
这次超模君一定会汲取教训，决定把这顿饭给赢回来的！
如上图所示，现有各棱长均为 a 的一个正三棱锥和一个正四棱锥，当将它们的一个侧面完全重合地粘贴在一起后，新形成的几何体有几个外露面？
这不是超模君最爱的空间几何吗？看来这顿饭是十拿九稳了。
作为一个优秀的数学系毕业生，超模君一眼就看出来这道题并非是“4+5-2=7”那么简单了。
小天肯定以为我会回答 7 个面，殊不知超模君早已看穿一切，并且还想到了最便捷的解题方法。
首先，这两个椎体粘贴在一起后，粘合处的两个面变成了非外露面，所以我们初步判定：新的几何体最多 7 个外露面（4+5-2=7）。
紧接着就是这道题的关键所在了，“面AEF”和“面ABE”这两个面，超模君越看越不对劲。
于是超模君脑海里就出现了这一幕：
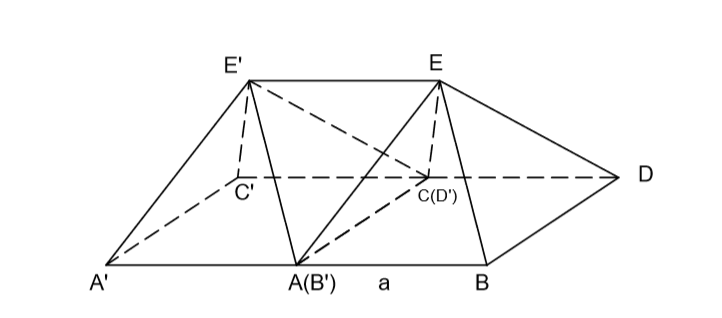
把两个正四棱锥并排放在一个水平面上，底边 B'D' 与 底边 AC 重合；
我们会发现两个锥体顶点距离 EE' 也等于边长 a ；
而两个正四棱锥中间的那个几何体 ACEE' 就正好是一个边长为 a 的正三棱锥；
此时，就可轻易地看出 面AEE' 和 面ABE 是共面关系了；
同理，面CDE 和面CEE' 也是共面的。
所以，最终结果是：新构成的几何体一共有5个外露面（4+5-2-2=5）。
于是，超模君拿着答案就找小天“要饭”去了。
可谁知道小天一脸坏笑：十八线网红呀，你又做错啦~
超模君看着屏幕里原题的答案：“4+5-2=7”。
怎么回事？
这是其中到底是哪个环节出了问题？
超模君的专业性居然受到了空前的质疑，看来今天必须要证明自己了。
果然，经过超模君的一番考究后，发现原来这是一道“历史难题”，这道题的出处最早可以追溯到1980年推荐阅读《写给青少年的数学故事》
当年美国举办的“全美初级数学能力测试”中就首次出现了这道题目，而且参加这场测试的是数以百万计的高中生。
美国有个“全美优秀学生奖学金计划”，就是从“学术能力测验”中选拔出15000名学生，然后再从中筛选出4700个名额，每年颁发250~2000美金的奖学金；
而“初等学术能力测验”就是“学术能力测验”的预考。
当时考试主办方给出的标准答案是：“7个面”，而且大部分考生写的答案也是“7个面”。
但是，有个叫丹尼尔·洛文的17岁小伙却写了“5个面”，并且认为自己的答案才是对的，而“标准答案”和绝大多数人都错了。
为了求证此事，丹尼尔把想法分享给了父亲（丹尼尔的父亲是一名杰出的工程师）。
在经过多次验证后，父亲也认同了丹尼尔的答案。与此同时，丹尼尔还用橡皮泥制作了模型验证、演示给老师们看，并将事情反馈给了主办方。
丹尼尔成为了多年以来第一个质疑主办方的高中生。
真理是不可磨灭的，几经周折后，主办方最终还是承认了丹尼尔的答案才是正确的。
事实上，当年那场考试有大约24万人给出的答案是“5个面”，因为丹尼尔这一闹，最后主办方都帮写“五个面”的考生加了分，但由于人员基数过大，写“7个面”的几十万考生们也没有被纠错、扣分。
也许就是因为当年主办方的“心慈手软”，导致“7个面”的答案如今还在流传。
所以，为了守护数学的严谨性，超模君打算用数学方法正式解答一遍，也好让小天输得心服口服。
为了计算方便，不妨设边长 a=2。
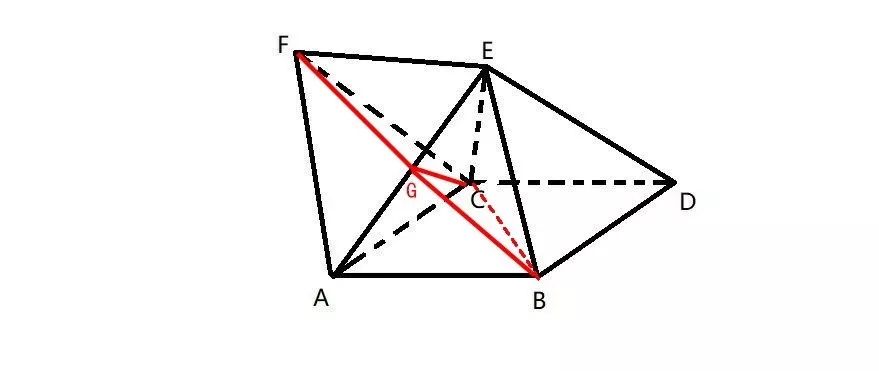
取 AE 的中点 G，分别连接 G 与 F、C、B 三个点；
显然 FG⊥AE，CG⊥AE，BG⊥AE；
所以，GF=GC=GB=√3，FC=2，BC=2√2；
再利用余弦定理（a² = b² + c² - 2bccosα）；
求得，cos(∠FGC)=1/3，cos(∠CGB)=-1/3；
所以，CG⊥GF，CG⊥GB（两个都为直角）；
显然，FAEB四点共面；
同理得，CDEF四点也是共面的。
终上所述，这道题的正确答案是：新形成的几何体共有 5 个外露面。
超模君看着小天：吃饭的地方，你挑还是我选？
在这里，超模君不定期会有脑洞大开，和你分享一些新研发出来的，小而美的，有故事的，有知识的理工创意产品，期待与您分享。微信又双叒叕改版了，还没把我们公号标星的读者，可能会越来越收不到我们的推送了
