期权交易中的关键之一是预测期权价格中的隐含波动率,简称“隐波”。这是因为交易员经常采取所谓的delta-neutral (德尔塔中性)策略,即在期权和现货两头分别做多或者做空,使投资组合的未来收益不随现货价格变动而变动,而只受到现货波动率变动的影响。
因此,德尔塔中性策略的收益取决于隐含波动率与未来已实现波动率之间的差。这个差也叫做“
波动率风险溢价
” (volatility risk premium)。通过德尔塔中性策略,交易员想要赚取的就是市场对其所承担的波动率风险的补偿。
从这个意义上,是否能够准确预测隐波便是德尔塔中性策略能否成功获利的主要因素。业界和学界都围绕这个问题进行了大量的探索。本文为你介绍我在这方面的三篇研究成果。其中第一篇已经在2014发表于国际衍生品专门期刊 Journal of Futures Markets 上,第二篇正在该杂志上进行小修改,第三篇在国际重要金融期刊 Journal of Empirical Finance 上进行修改。以下分别介绍。
同一现货对应着许多期权合约,这些合约有不同的敲定价格 K 和到期日 T。因此期权的隐波往往是一个随时间变化的曲面,称为“
隐波曲面
”。曲面相对于敲定价格的截面就是
隐波微笑曲线
,而相对于到期日的截面就是
隐波期限结构
。
对这个曲面的预测有两种途径:一种是结构化模型,通过理论比如无套利原则对曲面的动态变化进行建模;另一种是参数化模型,不需要理论,尽量让模型参数能够较好地拟合和预测真实数据即可。两种途径各有优缺点:前者有理论基础,满足无套利条件等,但建模非常困难。据我所知,目前尚无成熟的隐波曲面动态模型;后者简单易懂,往往预测效果好,但不满足无套利条件,因而在使用时也有一定的模型风险。其实这两者之间的差异不仅仅在期权里面存在,在任何资产定价问题中比如利率模型都有着同样的问题。
我跟合作者的第一篇论文(The Nelson-Siegel Model of the Term Structure of Option-Implied Volatility and Volatility Components, 见文末参考文献)的想法起源于一个市场观察:即隐波的期限结构与利率的期限结构颇有相似之处。比如,两者都分长短期,且长期端都会趋于一个平稳值,期限结构在市场正常环境下都是递增的凹函数。因此一个自然的问题是:
能够用于模拟利率期限的参数模型是否可以用来模拟隐波的期限结构呢
?
为了回答这个问题,我们借鉴了利率期限结构文献中比较成熟有效的模型——Nelson-Siegel Model(见下图)。该模型的优势在于简洁,仅仅只需要回归估计三个参数,并且这三个参数分别对应利率期限结构的水平、斜率和曲度。更难得的是,这个模型的实用性又很强。
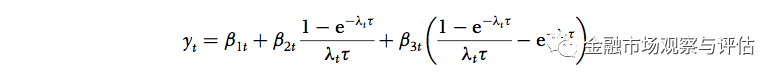
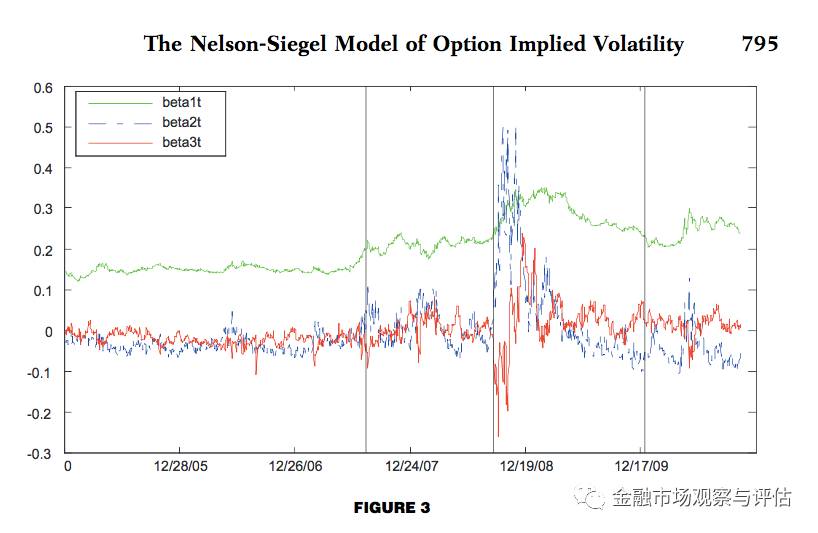
我们将这个模型对美国的指数期权数据进行拟合,发现了一些有趣的结果。比如,模型的第一个参数(下图绿线),估计出来以后发现跟隐波的平均值十分接近,可以被解释为长期隐波;第二个参数(下图蓝线),跟著名的VIX指数有超过 83% 的相关性,可以被解释为短期隐波;而第三个参数(下图红线)可以被看作是中期隐波。这三个参数可以决定一个隐波的期限结构。
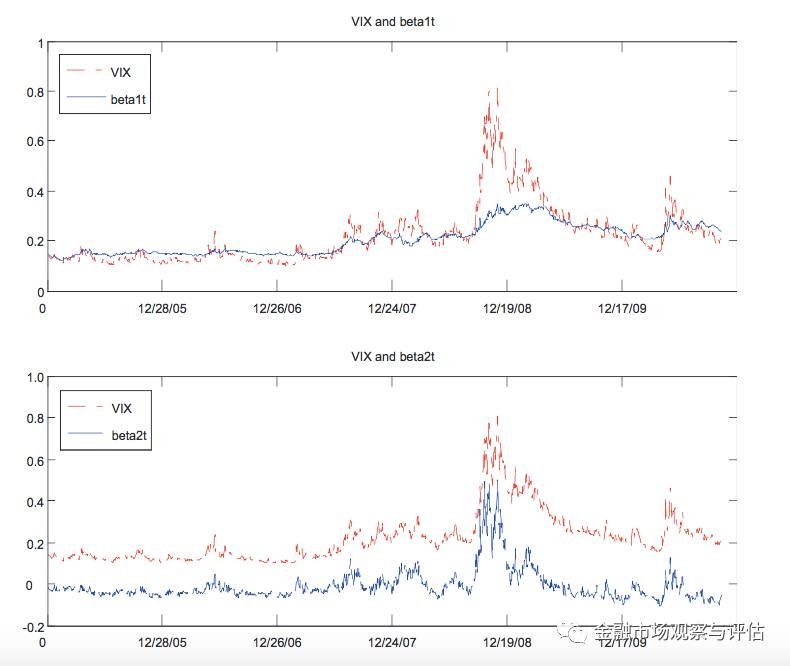
那么这个模型是否真的一点理论基础都没有呢?其实不然。我们在文章中证明,这个参数化模型其实对应于一个两因素的 Heston 随机波动率模型。即如果把传统的 Heston 模型中的随机波动率进一步拆分成一个长期均值项和一个中期项,那么这个两因素模型就等同于以上这个三因子的 Nelson-Siegel 模型。
当然我们最关心的是这个模型对预测隐波是否有益。为此,我们首先对提取出来的三个因子的时间序列进行建模,模型如下:
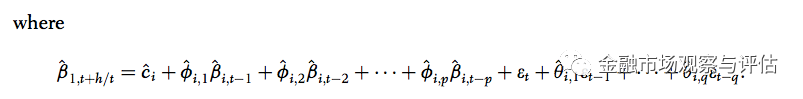
然后隐波的预测值就是:
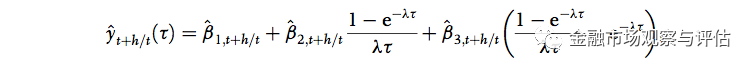
为了确认模型优势,我们将这些预测值跟两种模型进行比较。第一个模型是比较随意的一元二次方程,第二个是经典的随机游走模型,即假设隐波是不可预测的。样本外的结果显示,基于 Nelson-Siegel 模型的预测在统计上显著优于这两个模型。
总而言之,这篇文章发现,隐波期限结构可以通过一个Nelson-Siegel模型进行拟合和预测,模型中的三个因子分别对应于期限结构中的水平、斜率和曲度,也可以解释为长期、短期和中期隐含波动率。样本外的预测结果显示,隐波是完全可以被预测的。
下一期的文章将继续为大家介绍另外两篇论文。这两篇专门讨论隐波的预测,不但有统计意义上的预测,也有经济意义上的策略回测,对于实际交易具有很大的帮助。





