昨天《你要的数列放缩技术》谈到了两种常规的放缩方法.今天接着说说更有意思的放缩法——并项放缩法.
在不等式与数列求和的交汇处命制高考压轴题,成为某些地区高考数学卷的趋势.
所以,在两种基本放缩方法之上,还有很多变化.我们关于这一主题的系列文章会陆续谈到.
并项放缩法
看下面这样一个栗子.

从形式上分析,通项和等比数列比较接近,考虑朝等比数列去放缩,以利于求和.
可是,问题出现了.

奇数项和偶数项放缩的方向是相反的,我们无法逐项放大.
怎么解决呢?
我们把两项作为整体放缩——并项放缩.

下面要思考放缩方向.
根据题目要求,需要放大,则分母要缩小.
观察式子的特点,朝你要的数列放缩技术中的两种基本形式去放缩.

奇偶项讨论
注意到我们采用两项为整体分析的方法,所以求和时需要对n的奇偶分类讨论.

如果项数为奇数项,则最后一项保留.
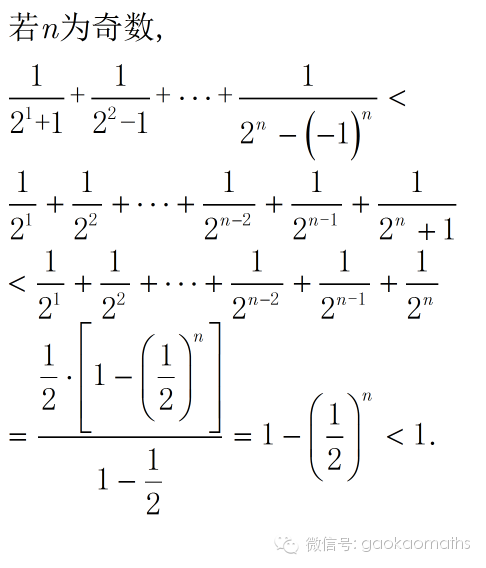
放缩法有很多变化,每篇文章积累一些,日积月累会逐步丰富自己的解题经验.
积累常见的用于放缩的不等式
今天要学习的放缩技术是:
1.若相邻两项或多项的放缩方向相反,可以把它们当做一个整体,研究这个整体的放缩方向,即并项放缩法
2.积累常用的放缩不等式.

如果把底数换成3呢?
思考1分钟.
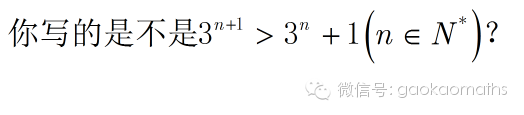
这个不等式没错,可是放的有些过了.

当然,我们也可以换一个放缩的角度.
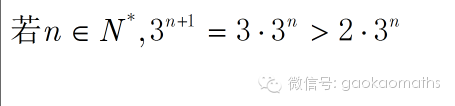
如果在实际解题中,发现这样放的过大,也可以往回收一些.

温馨提示:要获取微信公众号“高考数学左老师”的精华内容,可以回复“关键词”,你会获得一份关键词列表.根据这份列表,回复对应的关键词,就可获得内容.
推荐阅读:圆锥曲线综合题之定值问题
上一篇:二面角的平面角如何确定是锐角还是钝角?
--END--
苹果手机用户专属赞赏二维码






