惊！有人出生8年才第一次过生日！

很多脑筋急转弯的书上都有这样一个问题：有人出生4年之后才第一次过生日，这是怎么回事？

这个问题的答案不难：他是闰年的2月29日出生的。比如在2004年2月29日出生，以后连续三年（2005，2006，2007）都不是闰年，2月都只有28天，没有29日，他要等到4年之后的2008年2月29日才第一次过生日。

可是，如果我们说有人出生8年之后才第一次过生日。你相信吗？

如果你了解闰年的规则，就知道出生8年之后才过第一次生日也是可能的。比如，他在1896年2月29日出生。不但出生之后的连续三年（1897，1898，1899）不是闰年，而且第四年1900年也不是闰年，都没有2月29日，再后面的三年（1901，1902，1903）也不是闰年，直到他出生之后的第8年1904年才是闰年，1904年2月29日才第一次过生日。

闰年的规则是：如果年份数是4的倍数而不是100的整数倍，那就是闰年；如果年份数是400的倍数，那也是闰年。在其余的情况下，或者年份数不是4的倍数，或者年份数是100的倍数但不是400的倍数，那就不是闰年。

为什么要有这样的规则？我们知道，一年就是地球绕太阳公转一圈的时间。平均起来，一年等于365.2422天。在制定历法时，只能让一年的天数是整数，最接近一年的当然是365天，所以只能规定一年365天。但这样一来，每年就少了0.2422天，由1÷0.2422=4.12882知道：差不多每4年就少了一天。因此，每4年就补充1天。按照历法规定，当年份数是4的整数倍时，就在这一年的2月份末尾补充1天，就是2月29日，这一年就称为闰年。

但是，每4年少的天数实际上是0.2422×4=0.9688，每4年补充1天其实是多补了1-0.9688=0.0312天，经过1÷0.0312=32.0513个闰年之后，就多补了1天，应当将这一天扣除，也就是扣除一个闰年。每4年闰一次，经过32个闰年就是32×4=128年。这128年本应当有32个闰年，应当扣除1个闰年，只保留31个闰年。

如果规定每128年扣除1个闰年，这样的规定不容易记忆，使用起来不方便。所以采用了另一种方法：以400年为单位来计算闰年的天数。400年包含3个128年零16年。3个128年应当去掉3个闰年，因此，现行的历法规定，在这400年中，年份数是100的倍数的4个闰年中，只保留其中400的倍数但不是400的倍数的3个闰年去掉。

400年除了包括3个128年之外还剩16年没有加以考虑。经过128÷16=8个400年之后，积累起16×8=128年，从这128年的闰年之中应当再扣除1个。8个400年也就是3200年。不过，人类迄今为止使用公历的历史还远不到3200年。而且，真的经过3000多年之后的地球的转动速度也可能还会有微小的变化，一年是否仍等于365.2422天尚不清楚，所以现在去考虑那么遥远的未来的事情还为时过早，到时候自然会有办法。

这个问题的以上算法，其实与用最佳分数近似值去逼近π的算法类似。这里是用分母较小的分数去逼近1年的365.2422。首先是将1÷0.2422=4.12882用整数4作为近似值，得到

，

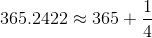产生4年1闰的规定。然后1-4×0.2422=0.0312的倒数

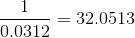
用整数32作为近似值，从而得到：

来源：选自《数学的神韵》，李尚志著，科学出版社。