原作者：Alon Amit ，来自：Quora，
翻译：南京大学科幻爱好者协会，镜子文明
https://zhuanlan.zhihu.com/p/33853851
一个常见题目，貌似易解的题目出发，发现背后竟然蕴藏了深奥的大道理。这其实是很多问题，尤其是数论题目的特点：很容易理解，但很难做。
在我碰到这道题之前，它已经被某人心怀恶意地发布在网络上，成为流行的朋友圈图片，肆意捉弄那些老实人
（Scridhar，这个人是不是你？）
。我根本没意识到我偶然看到的这道题到底是个什么样的怪物。它长这个样：
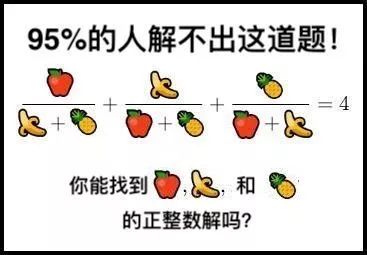
你可能已经在朋友圈看到过很多这样的图了，它们一般都是标题党的垃圾：什么“95%的麻省理工毕业生无法解决的问题”，这个“问题”要么很空洞，要么偷换概念，要么就是不重要的脑筋急转弯。
但这个问题不是。这张图片就是一个精明的，或者说阴险的圈套。
大概99.999995%的人根本没有任何机会解决它，甚至包括一大批顶级大学非数论方向的数学家。它的确是可解的，但那真的真的不得了的难。
（顺便说一句。发布的人实际上不是Scridhar，或者说不能怪他。）
你可能会这样想，如果所有的尝试都失败了，我们还可以直接用电脑计算大力出奇迹。这年头，写个电脑程序解决这种形式简单的方程真是太容易了，只要它真的有答案，那电脑最终一定会找出来。但很抱歉，大错特错。
用电脑暴力计算在这里毫无用处。
如果不把Quora的读者都当作椭圆曲线的入门者的话，我不知道怎么才能写出适合的答案。我在这能做的只是一个简要的概览。主要参考文献是最近Bremmer和MacLeod2014年在《数学和信息学年鉴（Annales Mathematicae etInformaticae）》上发表的一篇名为《一个不一般的立体代表性问题（An unusual cubic representationproblem）》的精彩论文。
让我们开始吧。
我们求解的是这个方程的整数解：
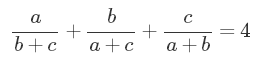
(为了与论文的变量名相适应，我把苹果、香蕉和菠萝修改过来了)
面对任何方程，你需要做的第一步是
尝试并确定问题背景
。这到底被划归到哪一类问题？嗯，我们被要求找到整数解，所以这是一个数论问题。就题而言，方程涉及有理函数
（多项式除多项式的函数形式）
，但很显然我们可以用通分移项的方法化成一个多项式函数，所以我们实际上解得是一个丢番图方程
（
Diophantine equation
）
。正数解的要求有一点不同寻常，接下来我们会看到这个要求会让问题变得多么难。
现在，我们有了多少变量？这个问题看起来很蠢：很明显，我们有三个变量，分别是a、b、c。让我们慢一点来。一个科班出身的数论学家第一眼就能察觉到，这个方程是齐次的。这意味着如果（a，b，c）是方程的一个特解的话，那（7a，7b，7c）都是它的解。你能看出为什么吗？给每一个变量乘一个常数没有改变方程的结构（7只是一个例子），因为分子分母全部都约掉了。
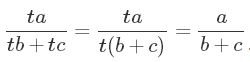
这意味着这个方程看上去像是三维的，但它实际上只有两维。在几何学中，它对应着一个面
（一个三元方程一般定义一个两维的面。一般来说，k个n元方程定义一个d维的流形，d=n-k）
。这个面是由一条过原点的线旋转形成的，可以通过截取的单平面来理解。这是一条投影曲线。
在大多数初等的情形，这种降维可以这么解释：无论解是什么，我们都可以分为两类，c=0的情形和c≠0的情形。第一类仅仅涉及两个变量（所以自然是二维的），而第二类情形我们可以对所有解同时除以c并得到一个c=1的解
（注：在上上一段，我们已经说明了这样一组解也一定是方程的解）
。因此我们可以在c=1的情况下寻找a和b的有理数解，只要乘以一个公分母，就得到了a，b，c的正数解。一般来说，齐次方程的整数解对应一个低一个维度的非齐次方程的有理数解。
接下来的问题是：这个方程的次数是什么？次数指的是各项中最高的幂次，对于涉及多个变量相乘的项，幂次就是各变量幂次之和。举个例子，如果某项为
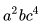，那此项的次数就是7=2+1+4 。
丢番图方程在不同次数难度完全不一样，宽泛地说：
一次的非常简单。
二次的也被理解得非常透彻，一般能用相对初等的方法解决。
三次的就是满山满海的深奥理论和数不胜数的开放问题。
四次的，嗯，真的真的很难。
我们这个方程是三次的。
为什么？嗯，去分母之后就很显然了：
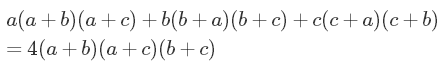
即使没有合并同类项，你也可以明白地看到次数为3：没有超过三个变量的乘积，最后我们得到的是类似a³ 、b²c、abc这样的项，而没有幂次超过3的。合并同类项后，方程整理如下
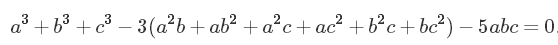
你可能会反对这样的变形：因为这样获得的解可能恰好使某个分母等于0，使得原方程没有意义。这是对的，我们的新方程的确有些解不与原方程对应。但这是好事。这个多项式形式给原方程打上了一些补丁使得它便于处理；对于我们找到的任何特解，只需要代入原方程检验一下分母等不等于0就可以了。
事实上，多项式方程很容易处理。比如说， a=−1 ，b=1, c=0。这是好事：我们有了有理数解，或者说有理点。这意味着我们的立体方程（3维）实际上是个椭圆曲线。
当你发现这个方程是椭圆曲线时，你会喜出望外，然后悲从中来
（注：这里不是大家熟悉的圆锥曲线中的椭圆，而是域上亏格为1的光滑射影曲线。对于特征不等于2的域，它的仿射方程可以写成：y^2=x^3+ax^2+bx+c。复数域上的椭圆曲线为亏格为1的黎曼面。Mordell证明了整体域上的椭圆曲线是有限生成交换群，这是著名的BSD猜想的前提条件。阿贝尔簇是椭圆曲线的高维推广。By 百度百科。）
，因为你发现椭圆曲线问题是个庞然大物（学渣哇的一声哭出来）。这个方程是一个展现椭圆曲线理论强大的经典案例，证明它可以被用来寻找一些爆难问题的解。
我们需要做的第一件事把椭圆曲线化成魏尔斯特拉斯
（注：Weierstrass，提起他最著名的成就就是严密化微积分的ε-δ语言）
形式。这是一个长得像这样的等式：
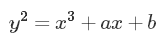
或者有时候也会化成
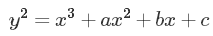
(这被称为长魏尔斯特拉斯形式。它并不是严格必需的，但有时候会带来一些便利)
众所周知，任何椭圆曲线都可以化成这种形式
（在特征为2或者3的域特别基础，如果你研究特征特别小的域，那结果就不一样了，我们此处不作讨论）
。如果想讲清楚怎么把椭圆曲线化成这种形式，那可就是长篇大论了（学渣的碎碎念：我信我信）。你只需要知道，这种变形是完全机械的操作
（关键在于方程至少存在一个有理数点，而我们已经确定了一个有理数点）
。现在有若干计算机函数包可以轻而易举地帮你搞定这件事。
但即使你不知道如何完成变换，验证它也是很容易的，或者说至少是机械的。对于我们而言，需要的变换由令人生畏的公式导出。
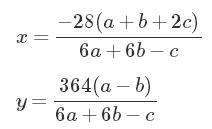
我知道这看上去就像随意的巫毒把戏
（注：巫毒，是目前最为人熟悉的非洲信仰，在西方文化中就是神秘力量的象征符号，可以类比国人心中的毒盅、赶尸和降头）
，但请相信我它不是。一旦你完成了这些变形，沉闷但异常直白的代数计算可以证明它是对的。
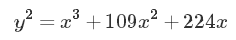
这个方程尽管看起来很原方程长得不怎么像，但确是如假包换的忠实模型。在图像上它长成这样，一条有着两个实部的经典椭圆曲线：
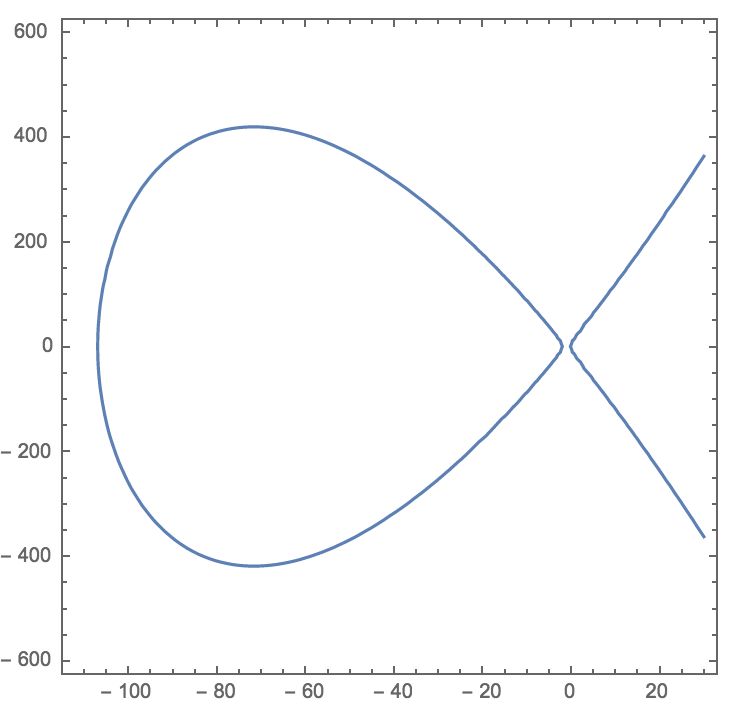
右边的“鱼尾”连续延伸至正负无穷。左边的封闭椭圆曲线也将给我们带来解决问题的惊喜。给定这个方程的任意解（x，y），你都可以通过下面的等式还原所求的a，b，c：
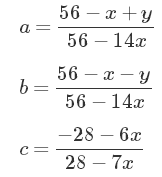
你需要记住，三元组（a：b：c）是用投影曲线理解的——无论你从这些方程中获得什么数值，你都可以随意乘上一个你想要的常数。
对于我们展示的两个图像，无论是从a，b，c到x，y还是反过来，都可以证明这两个方程从数论的角度是等价的：一个方程的有理数解可以导出另一个方程的有理数解。专业术语叫做双向有理等价
（
birational equivalence
）
，而这个概念在代数几何里面是一个非常基本的。如我们之前注意到的那样，可能存在一些不相互对应的特殊点，而情形是a+b，a+c 或者b+c恰好等于0 。这是构造双有理等价的必要代价，而不需要对此有任何担心。
让我们来看看手里的这个例子。它的椭圆曲线存在一个很好的有理数点：x=−100, y=260。可能找到这个点不太容易，但检验它在曲线上就很简单了：直接代入原方程检验等式两边是否相等（我不是随机摸的点，但各位不用关心这个问题）。我们可以简单地验证a，b，c代入的结果。
我们得到了a=2/7,b=−1/14,c=11/14，既然我们可以随意乘以一个公分母，那我们就可以变形为a=4,b=−1,c=11.
代入原方程，的确
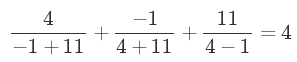
你可以很容易地验证。这就是我们原方程的一个简单整数解——但很遗憾，不是正整数解。找到这个解用手算不太容易，但用一点耐心即使不用计算机也不算太难。它将成为我们找到正数解的缘起之地。
现在，一旦你在椭圆曲线上找到了有理数点，如P（-100,260），你就可以利用弦切技巧进行加法，生成其它的有理数点（有理数的加法是封闭的，有理数加有理数还是有理数）。
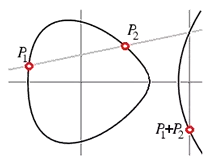
图解：椭圆曲线上点的加法
在任何情形下，在一个域（实数域R或者有理数域Q）中给定一个方程，解可以被视为位于R²
或者Q²的点（来自R²或者Q²的投影），而相加律就是弦—切结构的变形：
想要对两个点P₁和P₂做加法，首先构造一条过二点的直线（弦），若P₁，P₂重合，那么这条直线就是曲线的切线。找到直线与曲线的第三个交点P，对O和P重复上述操作，再次得到的交点就是P₁+P₂。当O点被选为无穷远处的点（一般都这么处理），图像就如上所示（注：至于O点是什么，这就涉及群论和更深奥的椭圆曲线知识，懂的自然懂，不懂的我也讲不懂，因为我也不懂）。更详
细的见原作者的Quora回答
previous
，再详细的请去翻代数几何。
一开始，我们可以通过作P点的切线，找到它和曲线再次相交的点，以此增加P点的值。结果看上变得有点吓人：
同样的，这个新的点也对应一组a，b，c的值：
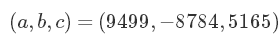
这个解用手算就很困难，但用电脑就是小意思了。然而，它还不是正的。
