
作者丨戴助教+本助教
编辑丨朱瑾
专栏丨九章算法
a. 给定一个无向图,这个图是在一棵树的基础上加上一条边构成的。问哪条边可以删掉使图重新变成一棵树?如果有多个答案那么输出输入的边中最后出现的那条。
b. 输入输出
Input:
[[1,2], [1,3], [2,3]]
Output:
[2,3]
Explanation:
The given undirected graph will be like this:
1
/ \
2 - 3
Input:
[[1,2], [2,3], [3,4], [1,4], [1,5]]
Output:
[1,4]
Explanation:
The given undirected graph will be like this:
5 - 1 - 2
| |
4 - 3
c. 注意给的边有顺序,当两个点已经有共同的根结点时候,这条边应该被删除
d. 输入保证[u,v] u
Ⅰ.
首先思考使用暴力方式解决问题,我们穷举那条需要删除的边,然后都过深度优先搜索(dfs)验证删完之后的图是否为一棵树,时间复杂度是O(n^2),虽然已经不错了,但这不是面试官预期的时间复杂度
Ⅱ.
我们换个思路考虑,遍历所有边,一边遍历一边将当前边加入到图中。如果我们发现,有一条边[u,v]还未曾加入到图中时,u和v就已经通过其他若干边相连,那么这就是我们要找的“多余”的边。
Ⅲ.
如果我们还是用dfs去判断u和v的连通性,那么是O(n)的时间复杂度,总的时间复杂度仍是O(n^2)。这里我们就要用到一种数据结构叫做
并查集
,可以在常数时间内两个元素是否在同一集合(查询操作)和把两个元素合并到同一个集合(合并操作)。在并查集中,每个集合都有一个代表元素,我们称之为祖先。
Ⅳ.
并查集的初始化
:在最初的时候,根节点都是自己,我们用一个数组parent[i]=i来表示这个关系。
Ⅴ.
并查集的查询操作:
每次给边的时候判断两个点的祖先节点,我们不停地通过调用parent函数向上寻找直到parent[i]==i
Ⅵ.
给出一条边,两个节点设置为l ,r 如果祖先节点father_l, father_r 不相同,说明此时l和r不向连,这条边信息有用(不是一条多余的边),我们就通过
并查集的合并操作
将他们连在一起
。
具体操作需要将祖先节点接在一起,令parent[father_r]=father_l。
Ⅶ.
路径压缩优化
:在做查询操作的时候我们将parent[now] = find_father(parent[now]),是为了压缩路径,因为一旦两棵树合并,其中一些节点不是直接指向根节点的,不合并每次搜索会浪费大量时间
Ⅷ.
我们认为总的时间复杂度是O(n),其中使用了路径压缩的并查集的常数非常小可以忽略
Ⅸ.
虽然题目强调如果有多个答案输出最后一条,但用上述方法只会找到一条“多余”的边,所以代码中是从前往后遍历所有边
http://www.jiuzhang.com/solution/redundant-connection/
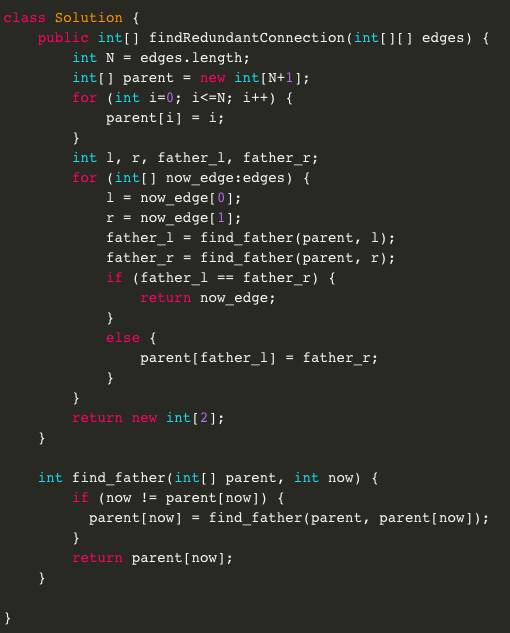
本题是一道中等偏简单难度的题目,
难点在于
用到了比较高级的数据结构:并查集,且需要把并查集应用在具体题目,来帮助我们快速的判断图中的连通性。
a. http://lintcode.com/en/problem/connecting-graph/
b. http://lintcode.com/en/problem/connecting-graph-ii/
c. http://lintcode.com/en/problem/number-of-islands-ii/

-
回复“简历”,查看简历撰写指南,获取“简历模板”
-
回复“冷冻期”,查看北美各大IT企业冷冻期信息和注意事项
-
回复“Career”, 查看Caireer Fair 攻略 check list
-
回复“薪资”,查看北美各大IT企业New Grades Engineer 薪资水平;
-
回复“项目”,查看7-14天可以搞定的小项目推荐
-
回复“评分”,查看系统设计评分指南
-
回复“behavior”,查看behavior interview指南
-
回复“晋升”,查看Engineer晋升机制
















