【
时间变更通知
:本周计算共形几何课程改至周六(2019年6月15日),上午9:00am-12:00pm,清华大学近春园西楼,三楼报告厅。敬请光临指导。】
在数学中,黎曼曲面理论玲珑剔透,精美雅致,从各个侧面体悟琢磨,都会有心得收获。一方面,黎曼面理论相对初等,可以从复变函数理论开始学习掌握;另一方面,黎曼面的初等理论可以用现代观点来重新审视和组织,从而让初学者得以登堂入室,领略现代数学的抽象概念。同时,很多基本数学分支在黎曼面理论上完美自然地融合:比如代数拓扑中的同调群、覆迭空间、纤维丛;微分几何的中的联络、曲率、陈类、Ricci流;偏微分方程中的椭圆型方程、热核、指标定理;代数中的域扩张理论、代数簇和理想理论,等等。
但是,由于人为的学科分割和专业壁垒,对于具有工程背景的学生而言,学习抽象的黎曼面理论依然有着本质的困难。如何将共形几何的精髓融入到计算机科学的知识结构之中,一直是老顾思考的一个问题。据老顾观察,理论物理专业学生掌握黎曼几何、纤维丛理论的速度要快于纯粹数学专业的学生。其根本原因在于物理的几何化发展使得物理专业的学生在脑海中储备了大量的实例,可以随时和抽象的几何概念加以相互验证。例如,纤维丛上的联络是费解抽象的概念,如果已经掌握了规范场的物理直观,理解联络就会直截了当。
令人欣慰的是,黎曼面理论中的重要概念和定理日益变得可计算,各种共形几何的算法不停地被发明出来,使得抽象概念的可视化程度不断提高,在工程实践中逐渐普及,很多工程应用触手可及,直观而频繁,这些都使得共形几何的学习难度有所下降。
老顾和很多学生深入交谈,他们都经历了长久的心路历程,困惑挣扎了数年,才逐渐认可内化了共形几何的语言体系和理论框架。在大家学习过程中,真正的转折点发生在动手编程,实现某个计算共形几何算法的时刻;或者在研究中遇到问题确实需要开阔思路的时刻。由此可见,动手实现算法,增加经验,学以致用是加快加深学习效果的不二法门。

图1. 基于共形几何的网格生成。
从工程角度而言,现实生活中的所有曲面都是黎曼面,很多工程问题的本质最终归结为共形几何。作为自然界的一部分,依随科技的发展、人类认识的加深,共形结构必然会在工程和医疗实践中发挥越来越重要的作用。例如在计算力学领域,有限元计算依赖于高质量网格,因此网格生成具有根本的重要性。如何将曲面进行三角剖分,使得每个三角形都接近等边三角形,一直是这一领域的基本问题。根据共形几何的单值化定理,物理世界中的所有曲面都可以保角地映射到平面区域。如果我们在平面上生成高质量网格,通过保角变换拉回到曲面上,就会生成高质量的曲面三角剖分。
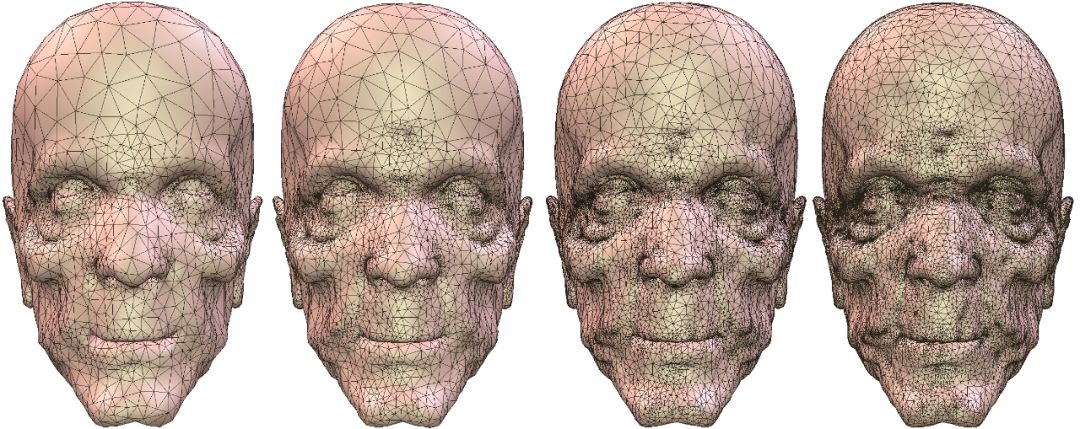
图2. 曲率测度收敛的离散曲面序列。
平面网格生成有很多算法,可以保证网格质量,例如Chow算法,CVT( Centroidal Voronoi
Tessellation)算法等等,因此,基于共形几何,我们可以生成高质量的三角网格,从而确保有限元计算的精度和稳定性。通过更为细致的分析,我们可以用
离散法丛的理论
证明如此得到的离散曲面,依随三角剖分的加细,其测地线、高斯曲率测度、平均曲率测度、Laplace算子都收敛到光滑曲面的相应几何量。
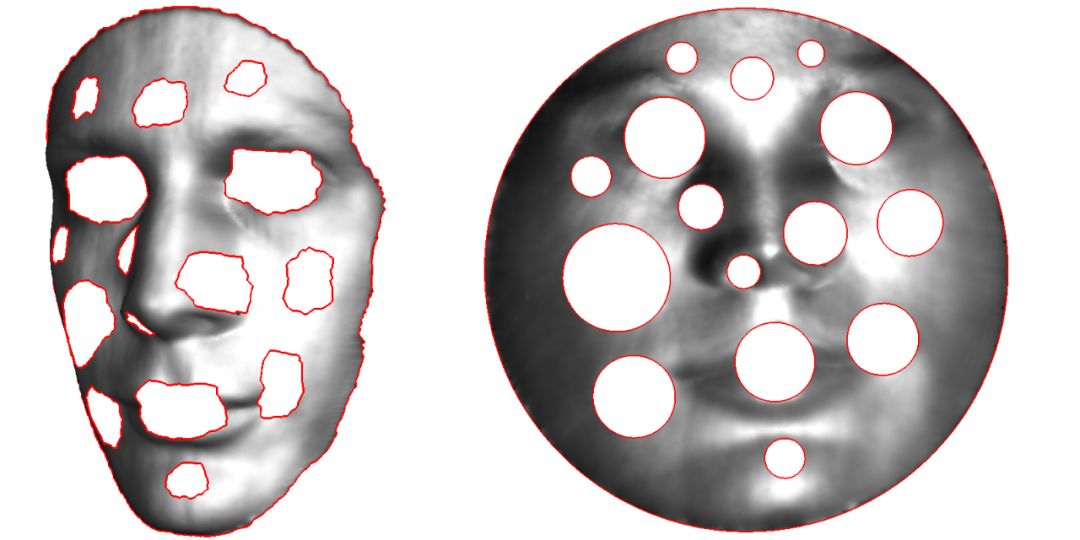
图3. 复杂拓扑曲面的共形映射。
目前,具有任意拓扑的紧度量曲面共形映射都可以计算。其中一类算法基于黎曼面的亚纯微分。黎曼面上具有给定零极点的亚纯微分存在性由黎曼-罗赫定理所保证。这次课程,我们来用初等方法来证明经典的黎曼-罗赫定理。虽然这一定理抽象深刻,其内在实质却是简单的线性代数。亚纯函数空间和亚纯微分空间都是线性空间,我们首先找到各自空间的基底,然后考察线性组合系数需要满足的条件,由此得到空间的维数。
黎曼面上有着丰富的亚纯函数,它们在加减乘除下封闭,因此构成一个域。如果两张黎曼面彼此共形等价,即存在保角微分同胚,当且仅当它们的亚纯函数域彼此同构。由此,我们看到共形几何与代数直接而深刻的联系。紧黎曼面上,如果两个亚纯函数具有相同的零点和极点,并且相应零极点的次数相同,则这两个亚纯函数之商为一常数。因此,亚纯函数的零极点包含了函数的几乎所有信息。
假设
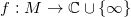 为一亚纯函数,在任意一点
为一亚纯函数,在任意一点
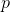 处的局部参数域内,其洛朗展开为
处的局部参数域内,其洛朗展开为
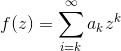 ,
,
如果
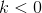 ,则
,则
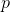 为阶数为
为阶数为
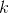 的极点;如果
的极点;如果
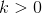 ,则
,则
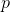 为阶数为
为阶数为
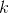 的零点。我们记
的零点。我们记
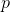 点的赋值为
点的赋值为
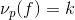 。
。
亚纯函数的除子为
 ,
,
这
 是函数在点p的赋值:在正常点处,赋值为0,在奇异点处,赋值为零极点的次数。给定一个除子
是函数在点p的赋值:在正常点处,赋值为0,在奇异点处,赋值为零极点的次数。给定一个除子
 ,这里
,这里
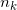 为整数,亚纯函数空间
为整数,亚纯函数空间
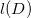 由所有的亚纯函数组成:
由所有的亚纯函数组成:
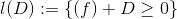 ,
,
这意味着亚纯函数的极点位置和次数由因子
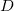 所限定。可以看出,空间
所限定。可以看出,空间
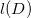 为有限维线性空间。我们类似定义亚纯微分空间:
为有限维线性空间。我们类似定义亚纯微分空间:
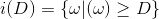 ,
,
同样
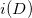 也是有限维线性空间。黎曼-罗赫定理给出这两个线性空间维数之间的等式:
也是有限维线性空间。黎曼-罗赫定理给出这两个线性空间维数之间的等式:
定理(黎曼-罗赫)
亏格为
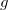 的紧黎曼面上,给定除子
的紧黎曼面上,给定除子
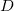 ,其决定的亚纯函数空间和亚纯微分空间维数满足等式:
,其决定的亚纯函数空间和亚纯微分空间维数满足等式:
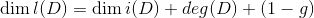 。
。
黎曼-罗赫定理在黎曼面理论中处于中心位置,大量的存在性证明都依赖于这一定理。它可以被视作指标定理的简单情形:黎曼流形上椭圆型偏微分方程解空间的维数由流形的拓扑所决定。
给定一张紧黎曼面亏格为
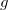 ,我们选取一组
典范基本群基底
,
,我们选取一组
典范基本群基底
,
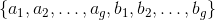
代数相交数满足条件:
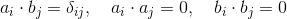 。
。
将曲面沿着基本群基底切开,得到一个
基本域
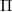 ,其边界为
,其边界为
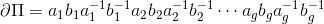
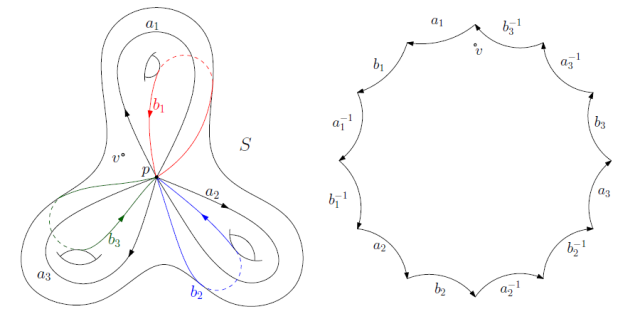
图1. 典范基本群的基底。
一个
全纯微分
的实部和虚部都是实的调和微分,并且虚部和实部共轭。由Hodge定理,黎曼流形上的每个上同调类都存在唯一的调和微分形式,因此所有全纯微分构成的群和上同调群同构,复维数等于亏格。我们取一组全纯微分构成的线性空间的基底,
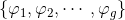 ,和基本群基底对偶,
,和基本群基底对偶,
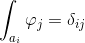 。
。
黎曼面上的
亚纯微分
(Meromorphic Differential)具有局部表示
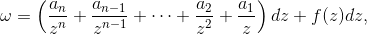
其中
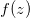 是全纯函数,前半部分是
是全纯函数,前半部分是
 的
主要奇异部分
,
的
主要奇异部分
,
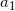 称为
称为
 在极点处的
留数
。
在极点处的
留数
。
 在所有极点上的留数和为零。
在所有极点上的留数和为零。
 沿着基本群基底的积分
沿着基本群基底的积分

被分别称为
 的A-周期和B-周期。我们可以将
的A-周期和B-周期。我们可以将
 进行如下的规范化:
进行如下的规范化:
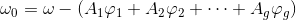
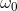 的A-周期为零,被称为
规范化的亚纯微分
。
的A-周期为零,被称为
规范化的亚纯微分
。
黎曼面上的亚纯微分(Meromorphic Differential)传统上也被称为是阿贝尔微分。为了研究方面,我们将阿贝尔微分归结为三类:
-
第一类阿贝尔微分是全纯微分,可以表示为线性组合
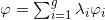 .
.
-
第二类阿贝尔微分所有极点处的留数都是零,一般形式为:
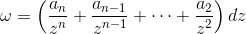
-
第三类阿贝尔微分存在非零留数的极点。
第一类和第二类阿贝尔微分之间存在
双线性关系
如下:假设
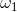 是第一类阿贝尔微分,具有周期
是第一类阿贝尔微分,具有周期
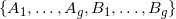 ;设
;设
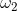 是第二类阿贝尔微分,具有周期
是第二类阿贝尔微分,具有周期
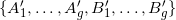 ,仅具有极点
,仅具有极点
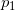 ,在极点
,在极点
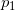 的局部参数域内,主要奇异部分为
的局部参数域内,主要奇异部分为
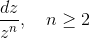
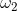 的存在性可以由Hodge定理得到。假设
的存在性可以由Hodge定理得到。假设
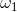 的局部表示为
的局部表示为
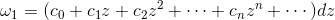 ,
,
那么我们有如下的双线性关系:
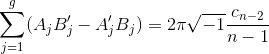 .
.
如果
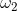 是规范化的亚纯微分,则
是规范化的亚纯微分,则
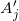 为零。
为零。
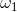 取典型基,不妨设
取典型基,不妨设
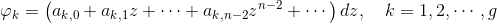
则有
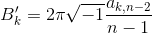 。
。
情形1:
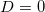 ,若亚纯函数
,若亚纯函数
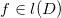 ,则
,则
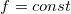 ,
,
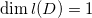 ;如果亚纯微分
;如果亚纯微分
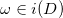 ,则
,则
 是全纯微分,因此
是全纯微分,因此
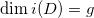 。并且
。并且
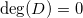 ,因此黎曼-罗赫公式成立。
,因此黎曼-罗赫公式成立。
情形2:整除子,即
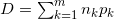 ,系数
,系数
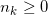 。如果亚纯函数
。如果亚纯函数
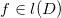 ,则
,则
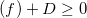 ,
,
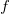 在
在
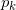 处的极点阶数不大于
处的极点阶数不大于
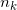 。考察
。考察
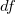 在
在
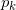 邻域的局部洛朗展开,则有
邻域的局部洛朗展开,则有
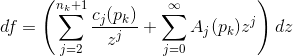 ,
,
令
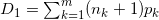 ,则有
,则有
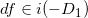 。由此,我们得到线性映射:
。由此,我们得到线性映射:
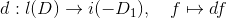 。
。
这一线性映射的核为常值函数,像空间记为
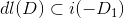 。
。
我们来构造像空间
 的一组基底。对所有极点
的一组基底。对所有极点
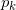 ,
,
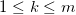 ,所有阶数
,所有阶数
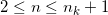 ,存在第二类规范化亚纯微分
,存在第二类规范化亚纯微分
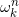 ,仅以
,仅以
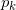 为n阶极点,在
为n阶极点,在
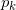 附近的主要奇异部分为
附近的主要奇异部分为
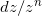 。
。
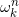 的A-周期为零。这样的亚纯微分共有
的A-周期为零。这样的亚纯微分共有
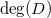 个。那么
个。那么
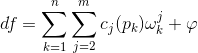 ,
,
这里
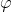 是全纯微分。因为
是全纯微分。因为
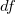 的A-周期为零,
的A-周期为零,
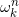 的A-周期为零,因此
的A-周期为零,因此
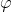 的A-周期为零,因此
的A-周期为零,因此
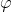 为零。由于
为零。由于
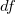 的B-周期为零,我们得到线性方程组:
的B-周期为零,我们得到线性方程组:
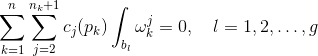
假设系数矩阵的秩为
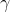 ,
,
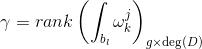
我们有:
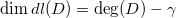 。更进一步
。更进一步
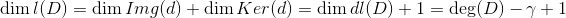
假设全纯微分基底为
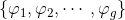 ,在
,在
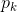 处的洛朗展开为
处的洛朗展开为
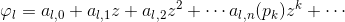 ,
,
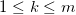 。
。
如果
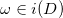 ,那么
,那么
 为全纯微分,
为全纯微分,
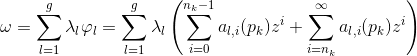 。
。
 以
以
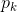 为零点,其阶数为
为零点,其阶数为
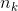 ,由此得到线性方程组
,由此得到线性方程组
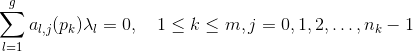 ,
,
设系数矩阵的秩为
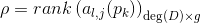 ,
,
则解空间的维数为
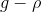 ,从而
,从而
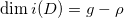 。
。
由双线性关系
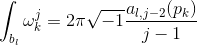 ,
,
我们得到两个系数矩阵的秩相同,
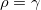 。因此
。因此
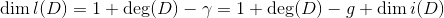
一般情形:我们任选一个亚纯微分
 ,则有
,则有
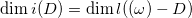 。黎曼-罗赫公式可以改写为对称形式:
。黎曼-罗赫公式可以改写为对称形式:
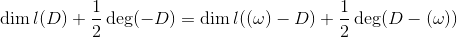 。
。
如果
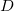 或者
或者
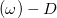 和整除子等价(即相差一个主要除子),那么黎曼-罗赫公式成立。
和整除子等价(即相差一个主要除子),那么黎曼-罗赫公式成立。
如果
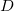 和
和
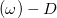 都不和整除子等价,我们可以证明下列条件成立
都不和整除子等价,我们可以证明下列条件成立
-
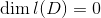 ,
,
-
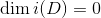 ,
,
-
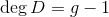 ,
,
因此黎曼-罗赫公式成立。
1)假设
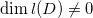 ,则存在亚纯函数
,则存在亚纯函数
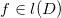 ,则
,则
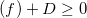 。令
。令
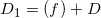 ,那么
,那么
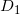 为整除子,并且
为整除子,并且
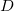 和
和
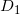 等价,矛盾。
等价,矛盾。















