
最近,我的一位朋友Z女士,因为她女儿的成绩问题经常向我抱怨。
“
我女儿以前成绩可好了,根本不用我操心,什么报班,都不用。怎么到了初中,数学下滑得这么厉害?”
“现在都初二了,果然女孩子在数学上的劣势就看出来了。”
“我跟她爸爸没少操心,给她报了辅导班,但老师的质量良莠不齐,很多就是给她不停地讲题,我女儿自然就学不进去。而且她的漏洞比较多,也不知道从哪里补起。”
“这次期中考试,她的数学成绩掉到了全班20多名,说她吧,她就特委屈和我说,好多题她做过,就是考试的时
候时间不够......还有题漏看条件......还有题计算很多,算错了一步......””
“我发现她什么都知道,但一考试就出错,真是气死我了!这初中数学究竟该怎么学啊?”

对于
做了多年教育的我,经常听到类似这样的抱怨。我只能苦笑着安慰她几句,毕竟这种问题不是一两句话就能指点迷津的。
的确,对于相当一部分学生来说,数学如梦魇一般缠绕左右,"上课认真听讲,课后按时完成作业,平时多总结,多思考,多练习。"这种“专家式”的废话早已详熟于耳,然而对大多数普通学生,这并没有什么用。
但数学这个学科又太重要了,
数学被称为学科之王,学校大都拿数学成绩来区分好学生跟差学生
,你也不能怪学校势利,数学如果没有学好,数学单科拉分大不说,还直接导致整个理科全部垮掉,整体成绩的分差自然会被拉的很大。
数学学习是很讲究基础的
,像建造一座大楼,自下而上,循序渐进,小学的数学没有学好,初中肯定学不好,到高中就会一塌糊涂,如果你这时还有机会上大学的话,大学里也会不断遭遇挂科的境遇。所以我们不能逃避数学,我们要找到方法
,将噩梦变美梦。

但其实数学并不难,作为一个智力普通的凡人,你完全可以将数学这头猛兽乖乖的驯服在脚下!
所以,我花了一天,专门整理了一下初中数学的学习方法和应试技巧,写下这篇文章,希望能对像Z女士这样的家长有所帮助。
什么是数学?
伽利略说数学是描写世界的语言!数学家斯托利亚尔说数学教学也就是语言教学。数学作为一种特殊的语言,精确,简洁而优美。同样,学习数学也应该是像学习一门语言一样,强调背诵和记忆。
说白了,一个字:
背
乍一听会觉得很荒谬,请听我慢慢细说。
大型考试的数学试卷中容易题:
中档题:较难题=5:4:1,
容易题+中档题=90%,
120分的试卷,其中108分都是正常人类可以对付的。
但绝大数人在80-90分之间
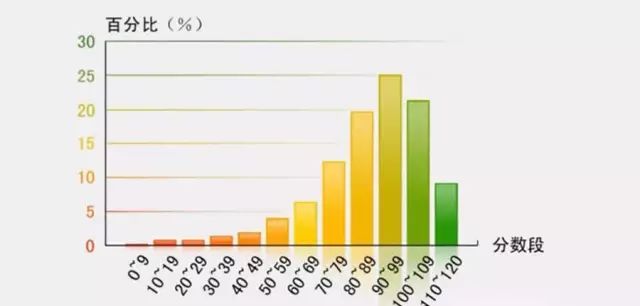
▲某市中考分数段分布图
平时学习也努力,脑子也不笨的同学是怎么考出80多分的成绩的呢?
三大难点
| 容易题白丢分 |
| 中档题乱丢分 |
| 较难题不得分 |
较难题,基本不拿分,平均下来要扣掉15分,
中档题中,扣掉15分,
简单题再莫名其妙扣掉5分,剩下也就只有区区85分了
而那些高分学生是如何做到的呢?
三大目标
| 容易题不扣分 |
| 中档题少丢分 |
|
高档题拿点分
|
正常发挥的情况下,
容易题得满分,中档题丢4分左右,较难题丢6分左右,总分120的数学就能维持在110分。
那么学生如何才能克服三大难题,
拿下三大目标呢?
★★★★★
1.“背”基本概念
2.“背”常用结论
3.“背”典型题目
★★★★★

好多题目考察的都是对
基本概念的理解程度和基本运算能力,是热身题,送分题,一定要照单全收
。
前提是要“背”数学中的基本概念。
数学教材中把重要的定义,定理,公式都用黑体字标出来了,虽然看上去简单,但不一定都会,要有足够的重视。
学生知道“-3“的绝对值是“3”,或是说正数的绝对值是它本身等等,依旧没说清什么是绝对值,
这些只是绝对值的代数运算,然而它的定义却在几何范畴
:
数轴上一个数所对应的点与原点(零点)的距离叫做该数绝对值。
我们来看一道关于初学绝对值的难题:
当代数式|x+1|+|X-2|取最小值时,相应的x的取值范围是多少?
在不了解定义的情况下,学生会想尽办法的用不等式的知识去做,然而知道了定义,自然而然就会想到
画数轴
,题目就能迎刃而解!
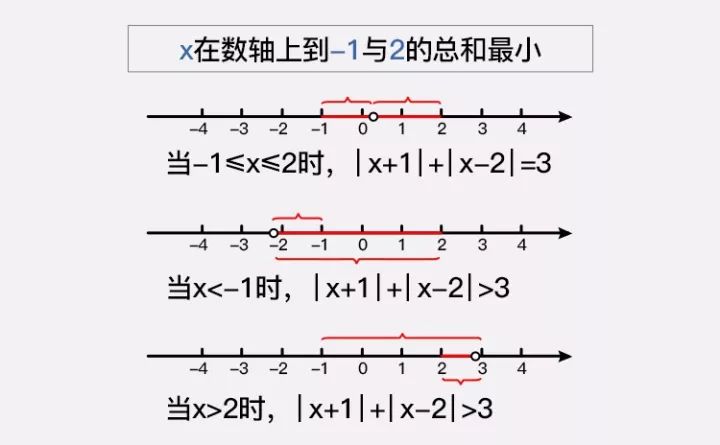
类似的定义还有:一元二次方程的定义、函数的定义、二次函数的定义等等,背熟了概念,题目感知难度与熟练度
下降好几个梯度!
案例:
我之前教的一个学生,初中数学就是
80
多分的水平,每次考试完总是信心满满的,
110
分没有问题,可是试卷发下来就彻底打回原形,才
8,9
十分,什么原因呢?他的解释是太粗心,其实都会做的,我说不是,是你的基本概念搞了个半吊子,我将它的
整个初中基本概念梳理了一遍,确保每一条概念都能正确的理解,并做到倒背如流。并针对每一个知识点选取典型题组反复训练,一个月后分数就能稳定在105分左右
, 甚至一次模拟考中取得了
119
的高分,三个月后的中考数学也拿了
107
分的满意成绩。

数学是一门精确的学科,每一个定义都是严格推敲出来的,
必须要牢牢地背下来,所有的解题都是基于这些公式定理。
就像学语文必须先记汉字,学英语必须先背单词。数学中的定理、公式就好比语文中的汉字,英语里的单词,一定要背
。
有些教育专家经常告诫大家,
数学靠理解,不需要死记硬背,但这颠倒了逻辑顺序,
先有背诵记忆,才会有理解应用,
况且理解是一个很模糊的概念,无法判断是否真的理解,这导致很多同学都有一种错觉,
觉得自己已经理解的很好了,实际上却是远远不够的。而背诵的标准非常明确,要么会要么不会。
“背诵在先,理解在后”,这个道理是显而易见的。
比如金庸的小说里就有类似的故事:在荒岛上,金毛狮王谢逊要将他毕生所学传授给年幼的张无忌。但时间紧迫,张无忌不可能慢慢理解内功心法。于是
金毛狮王就强迫他背诵,强行记住,不求理解。
等到张无忌长大成人,自然就慢慢领悟了这些心法,成为一代武学宗师。虽然本故事纯属虚构,但非常合乎学习的逻辑。
还有句话这么说,
熟读唐诗三百首,不会作诗也会吟
。小学的课本要求背诵很多古诗文,但很多同学并不能真正体会到其中悠远的意境和深刻的寓意。不过等你长大了,这些在你记忆深处的诗歌会在某一时刻迸发出来,你会突然领悟到它的美。
其实学习数学也是这样,
先
背诵
定理公式,这是理解的前提,有的时候甚至在做题的过程中才能领悟。
只要有足够的重视,背诵它们实在是太简单了,不像动辄几千的单词,大段大段的语文文章,所有初中数学的定义,定理公式加起来,用11张A4大小的复印纸就装下了。

案例:
小S是一个思维很敏捷,而又相当聪明的高三学生。但是快要高考的时候的几次摸底考试,150分总分从来没有考到120以上,问题是一张考卷几乎没有难倒他的题目。来我这辅导的时候,我让他把三角函数的所有公式默写出来,他说,哎,考卷上都有提供的,我干嘛要背呢? 我说你把焦半径的表达式写出来,他就在那里开始推算了。
2小时的考试除了答题,花大量时间重新去推理人类已经解决的数学难题,而且还不一定对!我给他列了五页A4纸张的考试常用结论,两个月后他就能稳定在140以上了。
我在上大学的时候,中国的教材看不懂,就会去翻国外的原版教材,国外的教材特点就是厚。曼昆的《经济学》英文教材有790页,原版的《大学物理学》教材有1060页,美国中学数学教材也有1400多页。厚不是因为难,而是详尽,如说明书一般
把所有常见的解题能用的结论通通列上去。
而
中国的数学教科书的特点却是言简意赅
,减负后似乎定理概念越来越少,更加精炼易懂,
然而无穷无尽的题目涉及到的都是衍生概念和公式变形!
这是中国自古以来的传统,孔老夫子的《春秋》用17000个字写完了242年的历史,然而《春秋左传》作为解读版,却有18万字,还是文言文。
其实重点中学老师和非重点的老师最大的区别之一就是
把教材外的常用结论、特定题型的标准解法都归纳总结给学生
。而平庸的老师只是照本宣科,完成教材上的教学任务,实质上学生还是不会考试!
所以
任何推论都必须背诵
,这样碰到选择填空题可以马上套用,一下子求出答案,而
在简答题中也可以减少我们思考的步骤和时间
,很多没有储备这些常用结论的同学,考试时就要从头思考,不仅速度慢而且失误率高。可见,背诵这些常用结论,会让你的思考走捷径。
天下没有不粗心的学生,只有方法不对的学生
,就像一个工人老是出错,但是你告诉他分解工序,如何拧好每一颗螺丝钉,错误率会大大下降。
背诵常用结论,就是分解工序的过程,把出错的环节给固定住,不给你犯错的机会
。
这些结论其实并不多,整个初中也就80多条。

学校里普遍采用的都是
题海战术
,各种各样的试卷,报纸,辅导书轮番上阵,做得你头大如斗,秉着“
做总比不做好,多做比少做好
”的思路,把有限的学习时间投入到无限的题海里。逼得学生叫苦连天,但是除了能让你看到数学题一阵恶心之外,收不到任何其他效果。
我们要学会抓主要矛盾。同学们的时间和精力都是非常有限的,要学会合理分配。
要想面面俱到还不如重点突破。
把80%的时间花在能出关键效益的2
0%的题目上,这20%的方面又能带动其余的80%
。
这个百分之20%的题目就是典型题
。每个章节都有核心的习题,这些习题涵盖了这个章节所有的出题思路,
除了要正确透彻的理解和掌握基本概念之外,还需要学生具备解题的能力与技巧
。
对于典型题,我们不能只做一遍,而是要一遍遍的去做,直到下笔如流。甚至有些不那么容易想到的解题思路,你要刻意的去背诵记忆。就像我上面说的,我是
反对题海战术的,提倡的是一题多遍,并且加以记忆
。
中考考试的时候不容许你每一题都有思考的时间,
中考中80%的题目都需要你不假思索的就要做出来的
,否则你根本没有时间对付那些剩下的20%的需要思考的题目。

那有的同学会问,命题老师出很多新题怎么办?要知道出全新的题目,又要出得好,是件非常困难的事情。绞尽脑汁地出全新题,一旦出的不好反而会被骂得很惨,这种吃力不讨好的事情命题人是不屑去干的。
对临近中高考的学生这个方法尤其有用
,为什么?他们思绪太多了,做的题如潮水一般。老是觉得数学太博大精深,搞了3年,还是看不到边。
但是背诵,熟悉典型题,就是把大海变成一个小池塘
。学生通常觉得,数学不可能背诵的,不可能把所有的题目穷尽的。
但其实数学的典型题就那么几道,抓住2,8法则的规律
,就会
简单很多。
掌握了典型题的解题方法和解题思路,就会自然而然地形成数学的解题思想。
整个初中就四大数学思想:数形结合,函数与方程思想,分类讨论思想,等价转化思想。
作为超级课堂的CEO,我一直在用我的理念打造一套最适用的初中数学套餐,终于经过团队的八年打磨,终于取得了成功。首先允许我介绍一下
超级课堂,它是全国首家中小学大片式在线教育平台,其中所有的初中数学课程
不是真人录播
,而是
以动画大片的形式呈现的
,
这也是为什么再不爱读书的初中生也愿意学超级课堂的原因
。

超级课堂走进杭州图书馆
学生们跪着也要看完
真人录播的课程中,虽然老师和画面是动态的,但再有趣的老师也不能让知识点动起来。不过超级课堂可以,
无论是审题做题时的易错点,还是理解层面的重难点,超级课堂统统让它们以学生最好理解的方式呈现出来:
动态审题过程、动画思维导图、清晰题目讲解
。连计算(移过等号加变减)都是会动的,这样孩子就不会因为任何一次跳步骤而听不懂了。
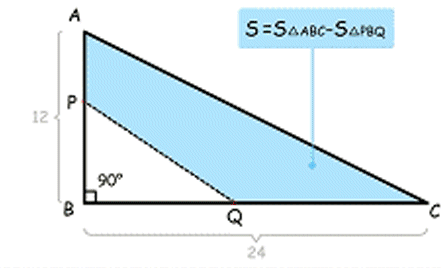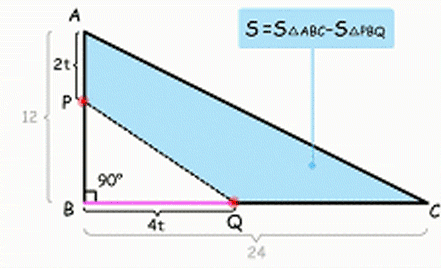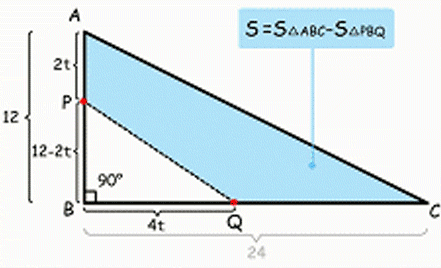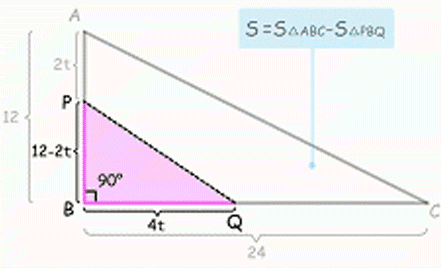
“背”基本概念
超课把每一个知识点做成动画,
展现一个
有趣
的课堂,帮助学生理解、掌握知识点,百分百背下基本概念!
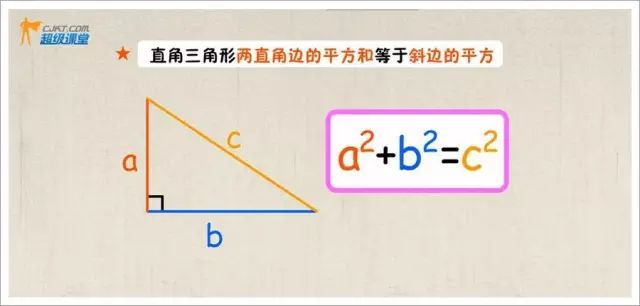
▲
勾股定理的基本概念
“背”
常用结论
超课研究各版本教材、课辅,帮助学生整理出最
系统
的常用结论,并加以推导与应用,常用结论不会漏!

▲
“
勾股树”n次展开公式
▲
勾股定理相关常用结论细目
“背”
经典题
众考所向,方为经典,超课整理上千套
模拟卷、中考卷,动画演示重难题型,必考题型,
高效
背下经典题!
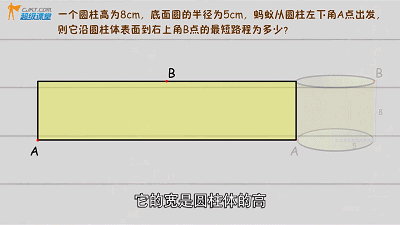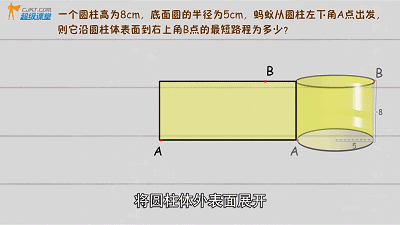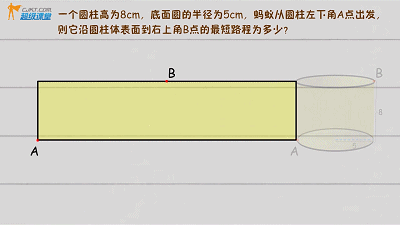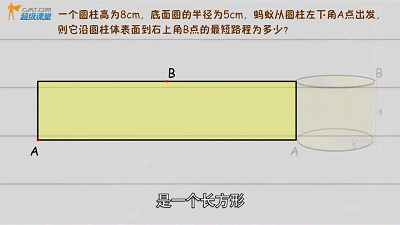
▲
勾股定理圆柱问题
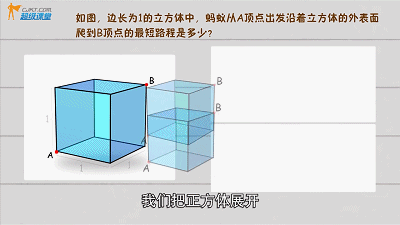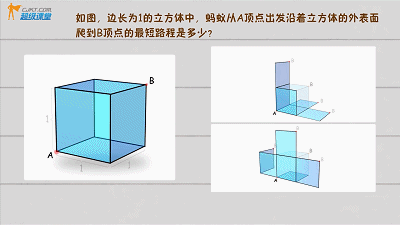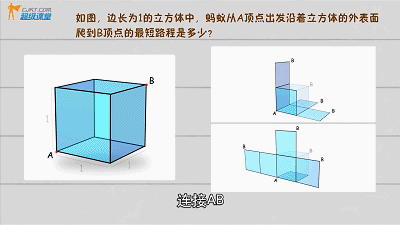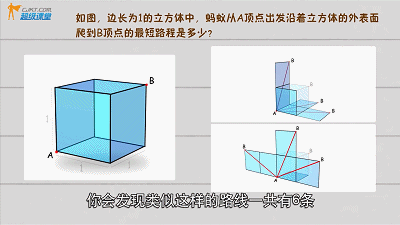
▲
勾股定理立方体问题

▲
勾股定理立体、平面结合问题













