鸡是常见的家禽,也是十二生肖之一。中国古代数学历史悠久,有很强的实用性,许多数学题来自生活实践,其中有不少题与鸡有关,例如人们熟知的“鸡兔同笼”问题。而在所有这些题中,最值得一说的其实是南北朝时期数学书——《张丘建算经》的最后一题。此题即是世界数学史上著名的“百鸡问题”,其影响贯穿古今中外。
中国古代数学题中有很多与鸡有关。例如,南北朝时期的一本数学书——《张丘建算经》最后一题是世界数学史上著名的“百鸡问题”,其影响贯穿古今中外。其题为:
今有鸡翁一直钱五,鸡母一直钱三,鸡雏三直钱一。百钱买百鸡,问鸡翁、鸡母、鸡雏各几何?

宋刻本《张丘建算经》百鸡问题
这就是说公鸡5钱1只、母鸡3钱1只、小鸡1钱3只,现在100钱买100只鸡,求公鸡、母鸡、小鸡各几只。显然,如果设公、母、小鸡各为x、y、z只,那么这是一道三个未知数、两个方程的不定问题:
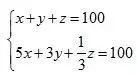 。但是,由于有了x、y、z都必须是自然数的约束条件,实际上只有有限组解。
。但是,由于有了x、y、z都必须是自然数的约束条件,实际上只有有限组解。
《张丘建算经》给出了这道题的全部三组自然数解,分别是:其一,公鸡4只20钱、母鸡18只54钱、小鸡78只26钱;其二,公鸡8只40钱、母鸡11只33钱、小鸡81只27钱;其三,公鸡12只60钱、母鸡4只12钱、小鸡84只28钱。
《张丘建算经》接着给出的“术”表明了各组解之间的关系:
鸡翁每增四、鸡母每减七、鸡雏每益三,即得。
这就说公鸡每增加4个(即增加20钱),母鸡就要减去7个(即减少21钱),小鸡就要增加3个(即增加1钱)。这一增减关系也是正确的,但是仅凭此无法得到全部解。现代数学解答此类不定方程问题,需要先求得一组特解,而后依据解之间的增减关系求得全部解,其形式大概是
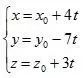 (t为自然数,
x
0
,y
0
,z
0
为方程的一组特解)。因此,我们可以说《张丘建算经》给出了正确解答及其之间的增减关系,但却没有给出求特解和增减关系的方法。后世对此问题的探讨沿着改进算题、求特解和求增减关系三条路线进行。
(t为自然数,
x
0
,y
0
,z
0
为方程的一组特解)。因此,我们可以说《张丘建算经》给出了正确解答及其之间的增减关系,但却没有给出求特解和增减关系的方法。后世对此问题的探讨沿着改进算题、求特解和求增减关系三条路线进行。
北周时期甄鸾所撰的《数术记遗》记载了另外两道百鸡问题,只是把鸡价稍微改变。分别是:公鸡5文1只、母鸡4文1只、小鸡1文4只,以及公鸡4文1只、母鸡3文1只、小鸡1文4只,均百文买百鸡。甄鸾给出的答案不完整,也没有给出解法,认为这种题只需要心算就可以了,“即舍数术,宜从心计”。
南宋的杨辉在《续古摘奇算法》中又搜集了两道百鸡类问题,不仅价格改变,而且物品种类也发生了变化。一题引《辩古通源》说温柑7文1只、绿橘3文1只、匾橘1文3只,百文买橘百只;一题说醇酒7贯1斗、行酒3贯1斗、醨酒1贯3斗,十贯买酒十斗。因为是三个未知数连动求解,杨辉认为此类问题是“三率分身”,后世称为“三色差分”。
明代中期吴敬在《九章算法比类大
全》((1450年))中
记载了一道类似的问题:“九文买个桃,二文买个梨,一文六个杏。百文买百枚。”程大位《算法统综》(1592年)对原百鸡问题稍加修改:“今有千文买百鸡,五十雄价不差池。草鸡每个三十足,小者十文三个只。”程氏还给出两道有三个和四个未知数的算题,分别是:“今有钱五十五两五钱,共买铜、锡、铁八万三千零五十…每银一钱买铜一百三十两,每银一钱买锡一百五十两,每银一钱买铁一百五十两”;“今有绫、罗、纱、绢一百六十尺,共价九十三两。绫每尺价九钱,罗每尺价七钱,纱每尺价五钱,绢每尺价三钱。”

现代学者李继闵(1938-1993)注意到上述时期的算题往往都有“百钱买百鸡,鸡母若干钱一只、鸡雏一钱若干只”的特点,把这一时期称为“百鸡术的古典时期”。
最早给出《张丘建算经》百鸡问题求特解方法的是唐宋之际的学者谢察微。他说考虑到小鸡1钱3只,那么把100÷9得到11余1,11就是母鸡数。第二步用9减去余数1,得到8为公鸡数。第三步100-11-8=81为小鸡数。最后依据增减率得到其他解答。合理化这种解法,大概可以说是先取100钱的三分之一33钱为母鸡价,除以3得到母鸡数。不过第二、第三步无论如何是说不过去的。谢氏的做法可以说是不切实际的算法浪漫主义。南宋杨辉沿用并改进了这种方法,先用试算的方法确定一个未知数,然后求得另两个未知数。其后吴敬、程大位等人解法都是沿用杨辉的思路。
明嘉靖三年(1524年),布衣数学家王文素完成《算学宝鉴》,对百鸡术有较大的推进。他的解法相当于先消去一个未知数,化为二元一次不定方程,然后通过试算求得一组解。王文素进而通过鸡值损益给出增减关系的正确算法。除此之外,王文素不满足“三率分身”,探讨了最高达七个未知数两个方程的“众率分身”的问题。虽然其算法仍然具有试算的性质,但王氏对百鸡问题的研究已经远超古人。为此,他得意地说:“愚乃玩之既久,得此拙法。虽十率以上亦可求之,岂止三率乎!”

布衣数学家王文素雕像
清乾嘉年间,百鸡术获得了进一步突破。中国古代一次不定分析的形式主要有三:第一,百鸡问题的三元一次方程组;第二,历法调日法求强弱之术中二元一次方程
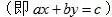 ;第三,《孙子算经》“物不知数”和历法求上元积年的一次同余方程组。从现代数学角度看,三者是相通的。不过在历史上认识到三者的关联却非易事。南宋秦九韶在《数书九章》(1247年)用大衍术解决了求同余方程组的问题,被世人称为“中国剩余定理”。李锐最先在《日法朔余强弱考》(1799年)中把调日法求强弱之术转化为同余方程问题。骆腾凤继而在《艺游录》(1815年)中也把百鸡问题转化为同余方程问题,用剩余定理求得一组特解,最后根据增减关系求得全部解答。由此,百鸡问题可以说获得了通解。
;第三,《孙子算经》“物不知数”和历法求上元积年的一次同余方程组。从现代数学角度看,三者是相通的。不过在历史上认识到三者的关联却非易事。南宋秦九韶在《数书九章》(1247年)用大衍术解决了求同余方程组的问题,被世人称为“中国剩余定理”。李锐最先在《日法朔余强弱考》(1799年)中把调日法求强弱之术转化为同余方程问题。骆腾凤继而在《艺游录》(1815年)中也把百鸡问题转化为同余方程问题,用剩余定理求得一组特解,最后根据增减关系求得全部解答。由此,百鸡问题可以说获得了通解。
清末丁取忠《数学拾遗》(1851年)先设一物为零,继而求解。受此影响,时日醇《百鸡术衍》(1861年)对百鸡问题进行了极致的探讨。时氏全书共28问,每一问给出两种解法。一种解法是对杨辉、程大位、丁取忠等人三色差分术的发展;另一种解法则把百鸡问题转化为同余问题求解,实际与骆腾凤相同。
1859年李善兰翻译了棣莫甘的《代数学》,现代代数方法开始为中国学者所熟悉。1876年知弥出版《一次不定方程解法》,是中国现代数论的先驱。此后,又有何维槔《百鸡术演代》、陈贤佑《增补百鸡术衍》(1899年)、陈志坚《演无定方程》(1904年)、张世尧《无定方程细草》(1910年)和《百鸡演代》(1911年)等相关著作,对百鸡问题的探讨逐渐融入现代数学。
值得一提的是,百鸡问题可视为中外数学交流的典范。印度、阿拉伯数学中都有一次不定问题。1202年,意大利数学家斐波那契在《计算之书》(Liber Abaci)中给出了一道“30钱买30鸟”的问题。其解法是用“合金法”,即相当于把1只公鸡和5只小鸡组合为6钱6鸡,把1只母鸡和3只小鸡组合为4钱4鸡,进而配比求解。这种解法思路与中国传统算法并不相同。不过,我们在清初李长茂所著的《算海说详》中看到了类似的思路。明末,西方传教士来华。李之藻与利玛窦合作编译《同文算指》(1614年),其中涉及到多道百鸡类问题。其解法是通过未知数的比率关系来求解不定方程,而不考虑其答数需要整数。这一做法也非中国传统思路。
西方学者Ulrich Libbrech和Jens Høyrup认为,古代世界数学的交流,往往只是传播算题,而非算法。这一看法很有道理。通过丝绸之路,一个数学问题往往容易以趣题或谜语的形式从一处传播到另一处,但是根植于整个数学系统的算法却不易理解和传播。因此,当地人往往会创造出足够的方法来解答传入的数学问题。百鸡问题大概就是这么一种情况。古代世界还常有一种“买马问题”。Jens教授认为柏拉图《理想国》(Republic)中似乎隐含有三人买马的问题;在丢番图《算术》(Arithmetic)中无疑已经有了此类问题。另一方面,类似的算题和算法也出现在中国古代数学经典——《九章算术》之中。
《张丘建算经》百鸡问题的解算主旨未明似是一种遗憾,但正是对其算法原意的探求,导致后世百鸡术之研究绵垣不断,众多奇异算法精彩叠现。一道数学趣题最终成为世界数学史上的华采篇章。
作者朱一文,上海交通大学科学技术史硕士(硕士论文:《百鸡术的历史研究》),中国科学院自然科学史研究所科学技术史博士,法国国家科研中心博士后,中山大学哲学系讲师,主要研究数学史与象棋文化。
来源:三思派
编辑:Alex Yuan
近期热门文章Top10
↓ 点击标题即可查看 ↓
1.
无数学不人生——原来数学讲的是满满的人生啊!
2.
二十个令程序员泪流满面的瞬间
3.
热烈祝贺赵忠贤院士荣获2016年度国家最高科技奖
4.
开年革命性发现:金属氢!百年理论终于完成向现实的华丽转身
5.
这个游戏没有玩家,为何在学术圈火了半个世纪?
6.
终于明白“女人如水”的含义 | 线上科学日
7.
物理界的华山论剑,一次会议聚集了地球三分之一的智慧
8.
这些大科学家的logo,你见过吗?
9.
人类为什么要为难自己搞出个闰年?
10.
一言不合折只鸡! | 线上科学日
点此查看以往全部热门文章






