首先看一个抽象函数的栗子:

分析:函数没有给出解析式,这是一个典型的抽象函数.常规方法无法入手,如何化抽象为具体呢?
采用特殊值法,对题中的x或者y进行赋值,既可以赋具体数值(比如令x=0),也可以赋变量(比如令x=-y).


用模拟函数增强预判
换个角度思考:抽象函数之所以让解题者难受,就是因为不知道函数的解析式.我们能否用学过的已知函数去模拟这个抽象函数呢?
哪个函数满足题中的这个性质呢?
答案是正比例函数.
因此求值域的问题只需要知道单调性就好了.
常见的抽象函数,都可以用学过的函数进行模拟
.具体情况可见下表:

有了这些知识做基础,处理相关问题就会容易的多.
比如下面这道题:

分析:由抽象函数表达式,可把f(x)模拟为以3为底的对数函数,由此能预判f(1)=0,f(9)=2,包括第二问不等式的解也能提前知道答案.当然我们不能直接把它当作对数函数,书面表达时要严谨.
如果本题为选择题或者填空题,解题速度将大大加快.

易错点:自变量都应该保证在定义域之内,这一点不能忘记.
方法小结
1.熟悉常见抽象函数的模拟函数
2.采用特殊值法,对x赋值,将抽象化为具体
3.多研究函数性质比如单调性、奇偶性相结合的问题的解题规律
一显身手
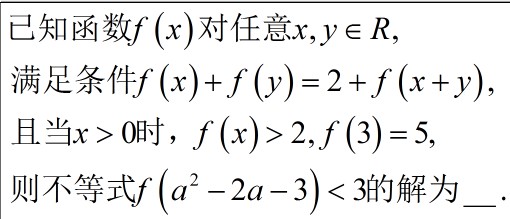
推荐阅读:
函数方程与图象变换
上一篇:
让你又爱又恨的定义域
--END--
苹果手机用户专属赞赏二维码





