这里的Xi呢,是由如下377个不同的指标构成(由于这些指标的scale不一样,所以依然需要对其normalization处理):
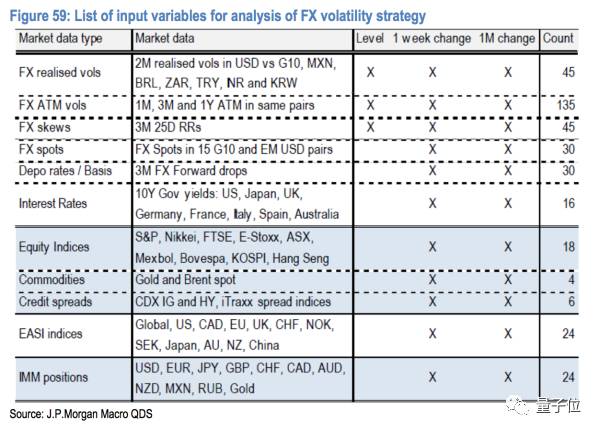
然后对于数据呢,我们是取的过去10年daily的数据,一共是2609个点。
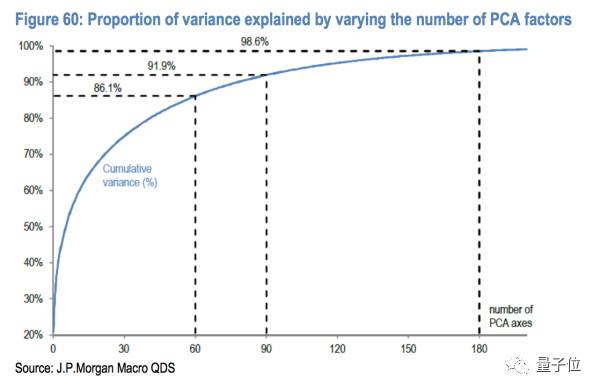
为了防止overfitting,我们用Principle Component Analysis(PCA,后面也会详细介绍)来对Xi进行降维(因为这里的Xi有370个,过于多了),我们通过PCA选取最重要的60个,90个,180个变量Zi(这里的Zi是由全部的Xi线性合成的大因子,被称作主成分因子)。如下图:
PCA呢,是一种对变量Xi非常多的情况进行降维的方式,下面unsupervised的统计方法里面我们会细致讲这个方法是具体怎么降维的。主要的思路就是将所有的Xi线性组合成若干个主成分因子Zi,使得其能最大程度的代表所有的信息。
上图表示的就是这些最主要贡献的Xi积累起来对于Y的解释程度,也就是这些选中的Xi所包含的信息能涵盖Y的多少信息。横坐标就是由PCA选出来的主成分因子的数目,纵坐标就是对Y的解释程度。
例如在图里我们可以看到,当我们选择前60个最大贡献主成分因子的时候,可以解释86.1%的Y;当增加到前90个因子的时候,可以解释91.9%;当选取前180个因子的时候,可以解释98.6%,相当于我们用了180个主成分因子就代表了原始370个因子的91.9%的信息,使得计算和model复杂程度都大大减少。
有些盆友可能会觉得有疑惑,前面的linear regression的lasso方法似乎也可以用来降维,为什么这里要用PCA这个方法呢。
我觉得有两个原因:
lasso方法需要利用连续的Y的值去做regression才能进行降维,而这里Y是分类不是数值,并且PCA的方法仅仅只需要Xi本身的信息就可以直接对Xi进行线性组合来降维。
第二个原因是这里的因子数目太多,有370个,如果用lasso的linear regression直接做回归会使得模型不稳定和过拟合。
对于数据,我们将其分成两部分,前8年的数据作为training sample,后2年的数据作为test sample,并且对于training sample用了10-fold cross-validation的方式去train model。
10-fold cross-validation其实是k-fold cross-validation中k=10的情况,其内容是将training sample随机均分成10组。然后每次选出一组作为validation set(其实也就是用来做test sample),这一组选出来之后剩下的数据全部作为training set来train模型,模型确定之后再应用在那选出的一组上求得MSE(可以当做test error)。这是一次实验。接着按照同样的方式将这10组的每一组都作为validation set进行同样的步骤,每一组都可以求得一个MSE的值。然后最终的结果就是将这10组MSE的值取平均,得到这个model最终的MSE。
但是这里为什么要用10-fold cross-validation我比较疑惑。或者说这里的10-fold cross-validation是用来得到10个Y的预测,然后平均一下得到最终的Y?
不太确定10-fold cross-validation是不是可以直接用来对Y求平均值。一般10-fold cross-validation只是用来求得平均的MSE,或者说根据某一个变化的参数画出来最小MSE时候(一般由于这个参数是penalty因子,代表的是bias和variance之间的tradeoff,自然MSE的图会是U型)这个最优参数的位置。
然后得到如下的结果:
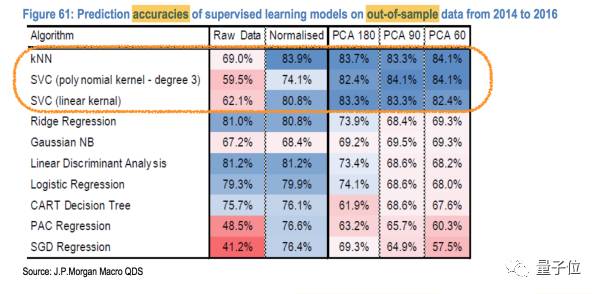
我们可以看到KNN,SVC(也就是SVM,kernel是三阶的polynomial方程)还有SVC(kernel是线性的方程)这三种model表现最好。
预测的结果跟现实的结果对比如下图:
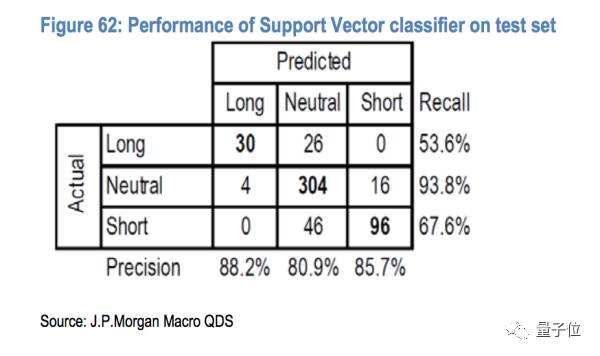
我们可以看到SVM的方法预测准确率还是比较高的(也就是一般预测的都是对的),但是抓住机会的次数(或者说预测trigger开仓的次数)不多。
所以策略的话可以着重利用高准确率这方面,或者重仓。
上面我们了解了两种处理classification问题的方法,一个是logistic regression,一个是SVM。他们的比较是当分类的点非常分散的时候SVM的表现更好(图上的表现就是相同类别的点会聚集在一起,并且不同类别的点尽量分开),当各个类的点混杂在一起的时候logistic regression更加合适(高度混杂在一起的时候SVM就无能为力了)。
SVM可以看作是一种空间上的mapping,所以当不同类的点被糅杂在一起而不是分团聚集在一起的时候(聚集在一起不一定是指在linear情况的在线的同一边,也可以是聚集成圆等等形状,通过mapping到另一个合适的更高维空间依然可以转化成linear的情况来进行处理,继而再mapping回去降维),会难以找到一个合适的映射空间处理问题。
2.5 Unsupervised Learning(包括期权相关科普)
Principal Component Analysis
Unsupervised方法和Supervised的区别呢,就是在应用的过程中有没有涉及到Y。
如果有Y,那就是supervised,更进一步如果Y的取值是连续的数值,比如涨跌幅度,那就是quantitative,比如regression的方法;如果Y的取值是discrete分立的类,那么就是qualitative,比如classification的方法。
如果没有Y,那就是属于Unsupervised方法。因为没有Y,所以Unsupervised的方法仅仅操作因子Xi本身。
这里unsupervised由于没有Y,所以并不像supervised一样是用于预测某个值或者某个类,而是主要是用于研究Xi之间的关系。所以Unsupervised方法有一个好处就是可以作为应用supervised方法之前对数据本身的预处理,数据本身的信息对于后期我们选择supervised方法进行预测Y有很大的帮助。所以unsupervised方法又起到exploratory data analysis的作用。
但是我们也要知道unsupervised方法有一个问题,正因为没有Y,所以我们没有办法像supervised方法那样验证我们的结果是否正确。
相对于supervised方法,unsupervised方法还有一个好处就是可以处理当因子Xi非常多(比如成百上千个)但是数据量又不是那么多的时候的情况。如果直接用传统的regression方法就会造成模型很不稳定,所以可以先利用unsupervised里面的Principal Component Analysis(PCA)方法将Xi进行降维,下面将会介绍到。
好了,大概unsupervised方法的背景就介绍到这,现在介绍一下其具体内容。
Unsupervised里面分为两块儿,一块儿是Factor Analysis,另一块儿是clustering。
首先呢,我们介绍Factor Analysis这一块儿,其中比较重要的Principal Component Analysis(PCA)方法。
为了更好的理解PCA的应用,首先简单介绍一下PCA的原理。
从名字Principal Component Analysis我们就可以大概看出来这个方法想干嘛,中文翻译过来叫做主成分分析。自然,其想要研究的就是主要的成分,换句话说,就是用最少的变量描述最多的信息 。
这里和前面lasso的方法有点不一样,lasso是直接把因子Xi前面的系数变为0,也就是直接把这个因子剔除的方式来给因子Xi降维, 而PCA是将很多的因子Xi进行线性组合,变成若干几个Zi来代表尽量多的信息。(这里一定要注意,PCA并不是像lasso一样将Xi的系数变为0的方式来降维,而是通过找到能最大代表数据信息的Zi,每一个Zi都含有所有Xi的信息,只不过他们前面的系数不一样) 。
因为如果当因子非常多(有些fund的strategy pool里有上百万个因子)的时候,我们可以通过PCA将这些因子构造成若干个主因子来进行操作。
并且在统计界有一个恐怖的传说,叫做”curse of dimensionality”。
因为因子Xi是我们人为主观判断可能会跟Y有关系才加上去的,那么有些人会想,因子的数目不就越多越好?毕竟最怕的就是在预测Y的时候没有将真正有贡献的因子考虑进来,前提错了的话后面不管怎么弄fancy的model都是错的,所以那如果把能想到的因子全部都加进去这样不就万事大吉了么,一个都不能少!
这样的想法是没错,漏掉重要的因子很可能会对Y的预测效果产生巨大的影响。但是凡事都是一个平衡,如果在模型里面因子加入了太多的话,即使把真的有贡献的因子加了进去,也会淹没在茫茫的因子中(因为加入的没有贡献的因子更多,并且由于每一个因子都有一定的权重会一起影响这个model,相对来看,有贡献的因子对于模型的解释能力其实是被稀释了)。
用统计的黑话来说就是,加入好的因子虽然会使得模型整体的bias下降(毕竟因子的信息更全面了),但是损失的是整个模型的variance会变大,也就是增加了其对于数据本身的依赖性,导致overfitting。特别是当因子的数目甚至大于我们数据点的数目的时候,那基本上无解了~(no kidding,是方程真的木有唯一解了…)
所以这里对于Xi降维的重要性就体现出来了,一个就是像lasso做的只留下几个能产生最多贡献的因子,另一个就是将所有因子线性组合成若干个可以代表这些因子信息的大因子,虽然这样同时也扔掉了没有被包括进来的因子可能包含的真实的有效信息,但由于减少不那么重要的因子数目,降低整个模型的variance,虽然会一定程度上牺牲模型的bias,但是总体来看效率还是提高了。
这样,通过PCA的降维方式,我们就更清楚数据信息背后的结构和主要的贡献来源,使得后续supervised方法的fitting更加有效率。
除此之外,PCA还能将这些主要的因子线性组合起来,变成若干个大的因子(实际上这些大因子就叫做Principal Components,主成分),用这些大因子代替之前的单个小因子Xi来尽量解释最多的Xi的信息。
因为同样对于高维(Xi非常多)的情况,还有一个问题就是当因子数目多了之后,因子之间的相关性问题会变得非常严重(我们可以想象因子足够多的时候,他们之间的信息很难会是完全exclusive的,特别是像金融市场,不同因子之间基本上都会有一定的相关性)。
一个解决办法就是将这些相关联的因子结合起来变成一个因子,也就是这里PCA可以做的事情。并且PCA可以保证这些得到的大因子之间是线性不相关的,也就是在方向上是垂直的。PCA通过正交变换将一组可能存在相关性的变量(若干Xi)转换为一组线性不相关的变量(变成Xi的线性组合Zi),除去对结果影响不大的特征,转换后的这组变量叫主成分。
好了,接下来就是数学上的解释了。为了避免公式的推导,直接用上图吧。
祭出遇到PCA必拿出来的一张图:
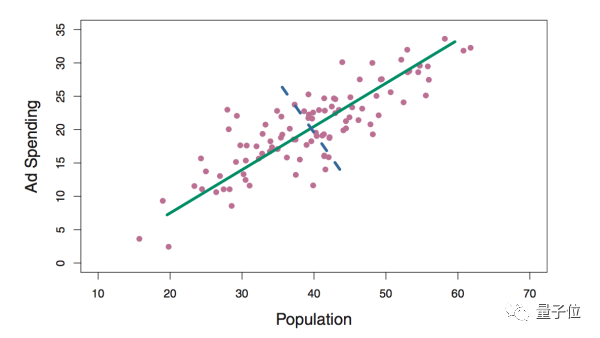
这里的横轴和纵轴分别是X1和X2两个变量,然后所有的点都画在这样一个二维的平面内。
现在呢,我们想要用一个变量去尽量包括这些点最多的信息,PCA也就是做这件事,图中的绿色哪条线就是PCA的结果。
怎么解释呢?
可以这么看,一个理解是最小二乘法,也就是这些点距离这条直线的距离最短,就像regression一样,最理想的情况就是这些点全部都在这条线上,自然这条线就能完全描述这些点的信息。
另一个理解就是最大方差理论,尽量使这些点在这条线或者说这个方向上的variance最大,也就是让这些点向这条直线做投影,要尽量使得这些点的投影距离最远。
为啥要最远呢?因为最远可以表示有更丰富的信息落在这一条线上面,这些点的区分度也越大。举个例子来说——
“举个例子,比如现在有10个人的数据,每条数据有两个维:出生地,性别,10个人的出生地各不相同,5男5女。从感觉上看,哪一维所包含的信息量大一些?是不是出生地呢?如果我一说出生地,是不是马上就可以找到那个人了呢?因此出生地各不相同嘛,而性别呢?因此性别只有2种,因此会有大量重复的值,也就是很多人的值都是一样的,这个属性对于人的刻画效果不好,比如你找一个性别是男的人,可以找到5个,这5个人从性别这一维上看,是完全一样的,无法区分。
从PCA的角度来看,出生地这个维的方差就要比性别这个维的方差要大,而方差大就说明包含的信息比较丰富,不单一,这样的特征是我们希望留下的,因此就这个例子来看,PCA更倾向于保留出生地这个特征。
那么是不是简单的就把需要保留的特征留下来,不需要保留的特征去掉就行了呢?比如说刚才那个人的数据的例子,是不是直接把性别这个特征去掉就完了?远远不止那么简单,PCA是把原特征映射到一个低维空间上,使得特征在这个低维空间中的方差最大,如果是直接去掉特征维的话,那么剩下的特征不一定是低维空间中方差最大的。
这里要注意一个问题,继续刚才那个人的数据的例子,有2维,性别和出生地,如果用PCA把它降成1维,那么这一维是什么?这是没有定义的,也就是说,这一维既不是性别,也不是出生地,它已经没有定义了,我们只知道它是1维选择出来的特征而已,但这并不影响我们对特征的使用。”
说了这么多,现在我们大概知道PCA是在干一件什么事情了,就是通过线性组合高维空间中Xi的方式构造出若干个Zi来对数据进行降维,并且找到尽量能代表所有点信息的几个主方向(也就是几个构造的大因子,一般第一个大因子包含的信息最多,然后信息度浓度次递减)。
好了,接下来说PCA的具体应用。
这里PCA是应用在期权的implied volatility surface上面。
首先我们来看一张implied volatility surface的美图:
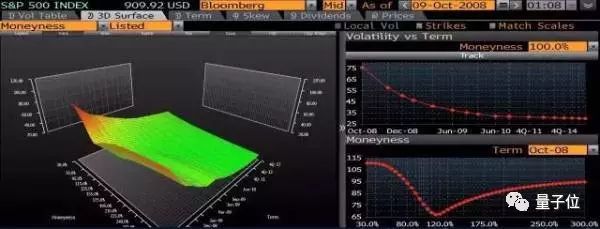
什么?又一脸懵逼?
看来这里需要稍微介绍一下期权才行呢…
首先,能读到这儿的我充分相信大家的实力,就直接上传说中的BS公式了(摘选自wiki)。
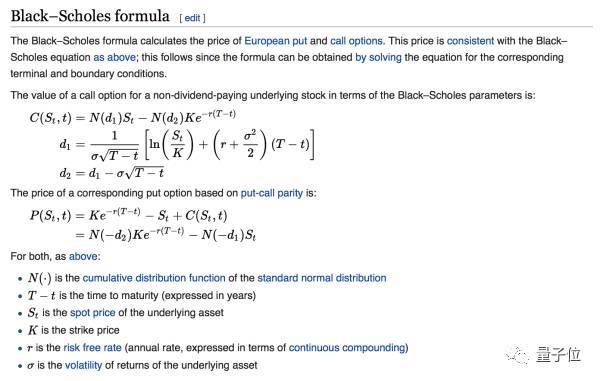
期权定价的核心几乎就是这两个公式,Call的定价和put-call parity的问题。
我们看第一个式子Call的定价C(St, t),我们可以看到这个式子中有5个参数。对于固定某个时间T,我们知道这个call的strike price执行价格K,也知道这个call的maturity到期时间(T-t),也知道risk free rate无风险利率r,正态分布N(·)的形式自然也都知道,剩下的就是volatility 𝛔不知道,所以现在我们就得到了一个volatility的方程来表示Call的价格C(St, t)。
volatility是一个什么东西呢?volatility是波动率,也就是期权underlying的标的价格的标准差。你如果问我标准差怎么算,我只能说去Google一下,计算讲的太细节估计都看睡着了…
所以假如我们知道volatility呢,我们就可以知道这个Call的理论价格,也就可以衡量当市场上Call的实际价格是高还是低,高了呢我们就可以卖,低了呢我们就可以买。
可惜天上不会掉馅饼,因为我们不知道volatility…
接下来还得知道BS公式的假设前提:

我们就可以看出BS模型的一个弊病了,那就是它假设underlying标的价格的波动率volatility是一个常数,跟strike price还有maturity没有半毛钱关系。
这明显是不符合实际情况的,因为市场会对对于不同的strike price和maturity有不同的预期和偏好,导致市场对于未来波动率的预期也会不一样。
但是! 我们虽然不能用波动率来算出来期权的理论价格,可是我们可以反过来呀~
我们有期权的市场价格,还有BS公式里面其他一系列的变量,比如strike price K,期权的maturity(T-t),也知道risk free rate r等等,就可以反过来求出来理论上的波动率。这样我们就可以知道市场对于未来的underlying标的的波动率预期了。
具体怎么算出来的,简单一点说就是当其他变量已知也就是固定的时候,期权的价格和波动率是一个单调递增的关系(如果对Greek有了解的,其实就是因为期权价格对波动率求一阶导的Vega是正值),所以不断试𝛔的值就可以最终match到当下的期权价格上面,自然也就是对应的波动率的解了。
看到这儿,很多人心里是不是在想,“尼玛,这货说了这么多,implied volatility到底有啥用?”
首先呢,implied volatility对于期权玩家的重要性不言而喻。
假设市场的每个参与者都使用BS模型定价,由于模型所需的其他输入值比如执行价格、所剩期限、标的价格还有无风险利率都是相对固定的,人跟人对于期权价格的看法就是取决于他们对于未来这个资产的波动率了。
假设有一个人巴菲特附体如有神助,对于未来资产波动率的预测百发百中如入无人之境,那么他(她)就可以根据自己预测的期权的价格跟实际的期权价格作对比来低买高卖,赚的就是别人对波动率的预测都很弱鸡。
但是可惜的是,这种外星人是不可能存在的,不然早就是世界首富了。当然如果有个人弄出来一个模型可以准确预测资产未来的波动率,那也超神了。
所以对于我们一般战斗力只有5的地球人怎么办呢?
我们可以反其道而行之,利用将已经是事实的市场的期权价格代入BS公式中算出来大家对于未来波动率的预期,也就是隐含波动率。因为期权价格是市场上供求关系平衡下的产物,是买卖双方博弈后的结果,所以隐含波动率反映的是未来市场对标的产品波动率的看法。
但是,算出来有什么用呢?
我们除了隐含波动率,还有一个波动率叫做历史波动率。这个东西其实算出来也挺简单的,只要我们有underlying标的的价格变化历史数据,就可以用统计的公式算出来标准差,也就是波动率。而且我们发现一件什么事情呢,那就是历史的年化波动率是处于一个区间,会有回归均值的一个特性(做swing交易的同学应该最熟悉了),并且离开越远回归的速度就越快。
比如说有一个股票,历史波动率都是在10%到30%之间,这样我们就可以知道从现在期权市场价格算出来的隐含波动率在历史上是处于高还是低的位置,同样可以做到低隐含波动率的时候买期权高隐含波动率的时候卖期权。
但这里有一个问题就是历史波动率的区间,不代表就真的不会飞出区间去,当发生重大事件或者传说中的黑天鹅的时候隐含波动率也会变很极端,比如Black Monday的时候飞到了150%,08年金融危机的时候也飞到了80%。
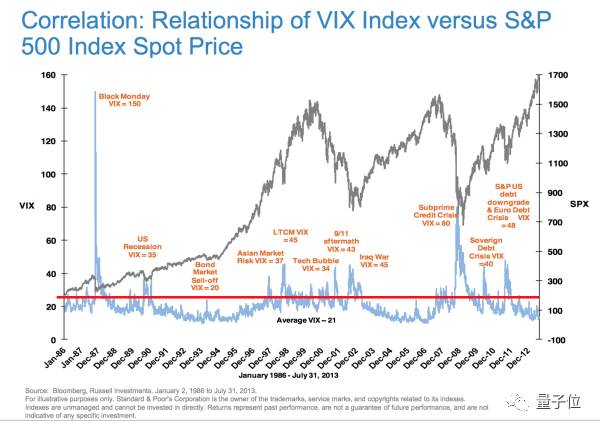
当然,做均值回归有点投机的感觉。有的同学可能觉得太low,我可是做价值投资的,只是想利用期权对冲一下风险。
同样,隐含波动率也很有用的!因为当确认了自己想投资的标的方向之后,可以把隐含波动率跟历史波动率作对比,权衡一下此时买入期权是不是划得来。也可以对不同strike price和maturity的期权进行横向比较,毕竟都是针对同一个资产,自然希望在满足了自己的需求买(卖)的情况下期权的价格越低(高)越好咯。
除此之外,对于直接交易underlying标的的交易员,我们也可以利用期权来帮助自己对标的的未来走势做出一定的判断。比如我们可以根据市场上对于同一个标的的所有不同strike price和maturity的期权价格,算出来每一个strike price和maturity对应的隐含波动率,其实也就是市场对于这个标的未来波动预期。
然后,将这个算出来的隐含波动率代入比如说隐含波动率二叉树模型,再算出来市场对于标的未来走势的预期,因为期权的价格本身就是已经是集中了市场上所有的有效信息,所以隐含波动率其实也包括了所有的博弈信息,利用其推导出来的未来走势就可以帮助我们对直接trade标的有一个大概的方向和市场预判。
好了,对于基本的期权概念应该有一个大概的sense了,接下来我们就来详细解释一下之前那张volatility surface的图。

(此图是在之前读伽玛交易员一篇文章存下来,08年危机时候的volatility surface,感谢之~)
期权交易员对volatility surface都会非常熟悉,因为这一定程度上就是自己根据市场情况做trade和进行风险对冲的基础。
volatility surface呢,是一个三维图,Z轴是隐含波动率,X和Y轴分别是moneyness和term(也许不同的软件会有不同的名字,这里借鉴Bloomberg的表示)。
moneyness的意思就是期权strike price和underlying标的的价格的ratio,这里以call为例,分为in-the-money(strike price小于underlying标的的价格,ratio小于100%的区间),at-the-money(strike price等于underlying标的的价格,也就是图中的ratio等于100%的位置)还有out-of-the-money(strike price大于underlying标的的价格,ratio大于100%的区间)这三种状态。如果是put的话strike price和underlying标的价格的关系则是反过来。term的意思呢,就是不同的到期日。
所以呢,我们可以把未来每一个到期日的每一个strike price和其算出来的隐含波动率画在一张3D的图上,这个就是volatility surface了。上图中右上角的是volatility VS term的二维横截面曲线,右下角是volatility VS moneyness的二维横截面曲线。可以说volatility surface包含了绝大部分我们需要了解的volatility的信息,而上面也介绍了volatility又是期权的核心,自然volatility surface的重要性也就不言而喻了。
既然volatility surface这么重要,那么如果我们可以预测未来的volatility surface是不是就相当于我们可以预测implied volatility进行交易了呢?

因为如果仅仅根据历史波动率进行交易,很明显我们丢掉了其他的很多有用的东西,仅仅只留下了波动率大小这一个信息。如果根据整个volatility surface的历史数据进行分析,对我们的预判的帮助会更大。在知乎上面看到说成功的期权交易,是做整个曲面的变化,这涉及的是曲面的smile/skew(下面会介绍),和曲面的整体高低位置,前者贡献利润的10%,后者贡献利润的90%。
好了,铺垫了这么多,接下来介绍利用PCA来分析volatility surface的信息。
这里选择的underlying标的是USDJPY(美元兑日元),至于为什么选这个,我感觉可能是想了解美日间carry trade的情况,而且日元是外汇市场非常重要的组成部分。
接着我们看看具体怎么将PCA应用在USDJPY的volatility surface上面。
volatility surface是一个三维的图像,Z轴是隐含波动率implied volatility,X和Y轴分别是moneyness和term。
对于PCA我们知道它做的事情是将所有的变量Xi线性组合成几个大的因子(主成分)Zi,所以问题就来了,我们的Xi到底哪些。
这里我们有的是implied volatility,moneyness还有term的信息。但我们并不能将他们全部作为Xi,因为虽然volatility是连续的数值,但term和moneyness的信息是固定的点。
所以我感觉这里有一个trick就是将每天的volatility的变化值作为Xi的值,而moneyness还有term的信息作为Xi的位置。
估计这么讲会有点混乱,画一张图就清楚了。
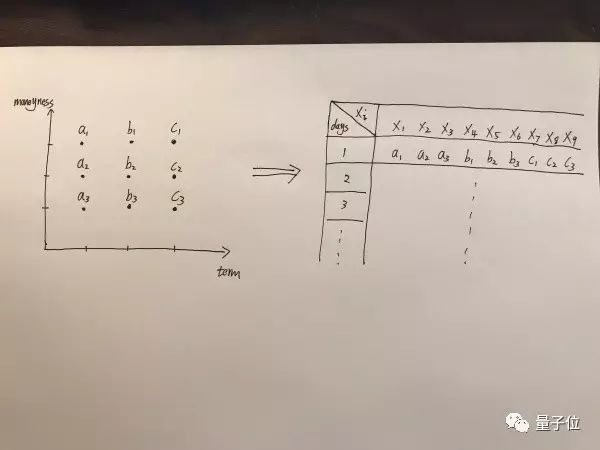
我们这里可以将所有的点都拉成一条线作为Xi,然后每天都有一列数据Xi。这样处理我们就将整个volatility surface变为了一列变量Xi,因为每天都有一个volatility surface,所以每天可以作为一个observation。
这样就将volatility surface的问题转化成了PCA的问题,我们想要找若干个由Xi线性组合成的大因子Zi,使得这些个Zi的方向最大程度的代表所有的点的信息(每天可以看做是这个Xi维空间上的一个点)。换做实际问题的解释,这些Xi的信息其实就是每天的整个volatility surface的信息,然后找到的由Xi线性组合成的大因子Zi的volatility surface可以最大的程度代表历史上所有天数的volatility surface的信息。
报告里面呢,选取了前三个主成分Z1,Z2和Z3,分别的图如下:
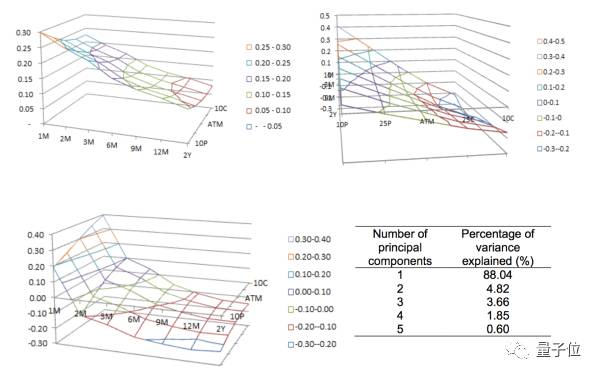
然后PCA还有一个好处呢,就是可以算出来每一个合成的大因子(主成分)对于所有点的解释程度(上图右下),也就是包含了数据中多少比例的信息。具体的方法叫做“proportion of variance explained(PVE)”,做法就是算出来这个大因子的variance和数据整体的variance之间的比例。
所以这里我们就找到了前三个大因子的贡献率分别是88%,4.8%和3.66%。
下图就是这三个主成分大因子在历史上不同时间的解释能力。可以看到第一个主成分的解释能力保持恒定,并且几乎都在80%以上。
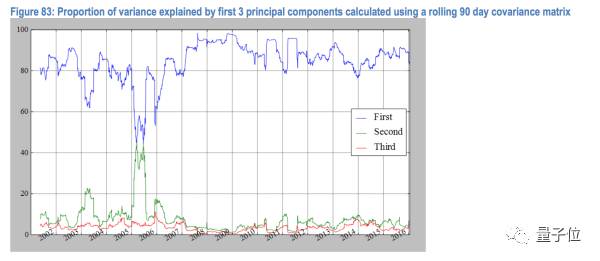
知道了能代表所有历史上volatility surface的这3个主成分之后我们自然能做的事情就很多了。
比如依据第一个主成分来判断delta hedge ratio(这里delta是期权价格对于underlying标的价格的一阶导,可以当做期权的价格对underlying价格变化的灵敏程度),也就是hedge delta使得整个portfolio独立于underlying标的价格变化(但实际上delta hedge只能解决一阶的hedge,二阶gamma的hedge因为是非线性所以只能依靠另外的期权来进行hedge)。还可以把前几个主成分单独拿出来,对剩下的residual做均值0的回归。
并且从这三个主成分大因子得到的volatility surface图中我们就可以看出来一些信息,对于固定maturity的情况下当moneyness是in-the-money的时候,implied volatility是很高的,说明了随着in-the-money的程度市场对于USDJPY的看跌程度是越来越大的。如果对于外汇市场了解的盆友可能就知道了,这就是因为日元往往被当做避险货币。
为了避免观众对外汇市场不熟悉,这里讲点日元这个特殊货币的背景,那就是日元具有避险功能。我大概总结了一下,仅作参考。
(1) 日本的常年低息政策,我们都知道在经济不好的情况下就会降息,如果已经是低息的话降息的空间就有限,利率降的越多货币越弱势,所以日元贬值的空间有限 。
(2) 同时也是由于日本低息的环境,所以国际环境好的时候很多人是借入日元然后买入其他高息的货币进行carry trader套利(就像美元QE的时候美国利息低大家会借入美元买入人民币投资中国市场),但是一旦国际环境恶化,买入的货币国家会实行降息然后贬值,投资的风险喜好也变为保守,这样套利就没有办法继续维持,大家就会卖出买入的其他国家货币然后买回日元还掉以前介入日元的债务,这样就进一步推高日元和日本的汇率,同时也压低其他国家的货币。
(3) 日本的不管政府或者民间的资本在国际环境好的时候喜欢投资海外的资产,譬如政府的养老金基金,当外部环境变差的时候,这部分资金也会卖出资产回流日本换成日元,即使不换回日元也会买入看多日元的衍生品(期权或者期货等)来对冲风险,都会进一步推高日元。
(4) 日元的池子大,流通性好,外部环境变好之后随时可以再卖掉。
(5) 大家只要一出事就做多日元已经是习惯了。。。所以形成了一个自我实现的循环。
其实上述对于固定maturity的情况下volatility随着moneyness变化的现象就是有名的“volatility smile(skew)”。具体这里不详细说,因为模型假设的是underlying标的的收益率并符合标准的正态分布,但实际上市场上由于不同的风险偏好产生了期权的尖峰肥尾现象,肥尾的方向也就代表了implied volatility的smile(skew)方向。产生的原因也有很多paper探讨,暂时没有一个固定的说法。也许后面有时间的话我会写一写期权的notes,不过看老板push我科研的程度了…
对于期权有一点需要注意或者可以利用,因为涨和跌并不是对称的,涨的时候总是缓慢的波动率低的,跌的时候总是摧枯拉朽波动率高的,期权价格呢又跟波动率有关,所以呢我们可以利用这一点。譬如说买put,一方面如果资产真的下跌,put本身由于moneyness和intrinsic value会增值;另一方面资产下跌的时候会引起恐慌增加波动率,也会使得期权增值,所以其实两方面的动力会一起做贡献让put的价格飞起来很快。
还记得前段时间的50 cent先生么?大家一开始都嘲笑这哥们脑子有病每天给市场送钱,现在才发现这哥们真牛逼。其实吧,他就是利用了期权波动率不对称这一点,疯狂在波动率低的时候扫货买便宜的put,一旦市场有点风吹草动导致哪怕一天的恐慌,向下的利润是非常丰厚的,远远超过前期裸买put的成本投入。
当然,别人是建立在对当时整个市场情绪非常敏感的正确判断前提下才敢这么单边做期权,还冒着成为各国基金经理永远嘲笑的二逼的风险,这种勇气我还是很佩服的,实至名归。对于不了解资本市场的同学呢,不要看了之后脑门一热以为股神附体就all in了,成功了是big short不成功就变big idiot,老婆本都亏光了不要怪我,我代表华夏三千万单身汉同志欢迎你的加入~
PCA除了在期权上面的应用之外,最常见的做法是用来分解portfolio的risk,也就是找到不同主成分大因子的beta(就是市场系数那个beta…)进行分配风险。大概的结论如下:
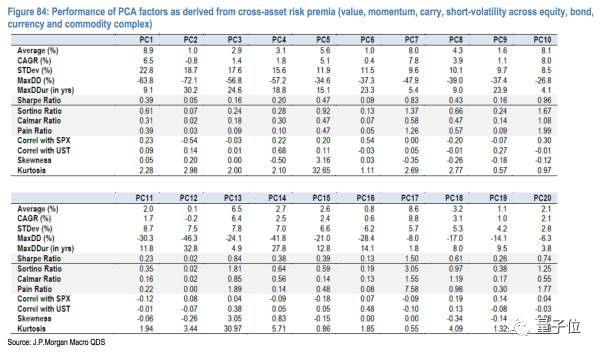
具体细节参见JPM在2013年的一个报告:
https://www.cmegroup.com/education/files/jpm-systematic-strategies-2013-12-11-1277971.pdf
好了,主要的统计方法和应用就讲完了。能读到这儿的简直真爱…么么哒!

原文长达5W字,由于篇幅原因,量子位(微信号:QbitAI)截取了第二部分与大家分享
点击左下角“阅读全文”,可以直接阅读完整文章。
有观点,有态度,愿你有所收获
【完】
一则通知
量子位正在组建自动驾驶技术群,面向研究自动驾驶相关领域的在校学生或一线工程师。李开复、王咏刚、王乃岩等大牛都在群里。欢迎大家加量子位微信(qbitbot),备注“自动驾驶”申请加入哈~
招聘
量子位正在招募编辑记者、运营、产品等岗位,工作地点在北京中关村。相关细节,请在公众号对话界面,回复:“招聘”。
△ 扫码强行关注『量子位』
追踪人工智能领域最劲内容













