卡尔曼滤波
老生常谈的,从运动模型开始
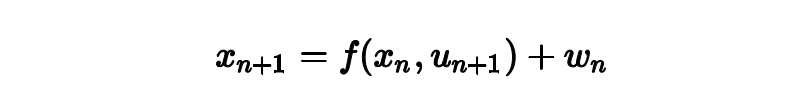
我们通过这个方程,构建了slam每一帧之间的关系,给一个输入u_{n+1},以及上一帧的状态x_n可以得到下一帧的状态x_{n+1} 的先验估计(如果还不明白先验估计后验估计的朋友,请观看黄老师带你飞公开课第三章的内容),当然w_n代表噪声
有了运动模型,我们同时也有观测模型
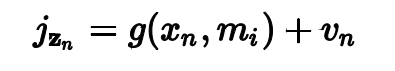
其中z_n=1_zn,2_zn...代表大量观测值,m代表地图上的点,g是传感器模型,v_n是噪声,有了这些模型,现在我们是时候来点概率论了
我们要计算x_{t+1}时刻的状态以及该时刻对地图的最新估计,根据贝叶斯公式:
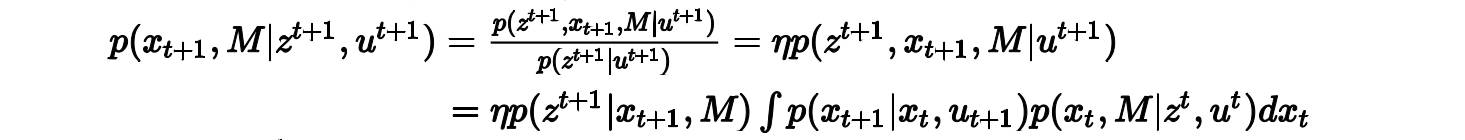
然后我们就上一个表,来吧这个算法的步骤简单列一下:

于是就是这玩意儿了,然后你假设了高斯分布,之后再把运动方程和观测方程线性化,就是经典的卡尔曼滤波了,注意,在这个过程使用到了边缘概率和条件概率的计算,这个计算方法在黄老师带你飞的课程第二章部分就已经讲过,我就不再复述了。
于是,你就有了对于一个这样的一个扩展卡尔曼滤波器,但是这个不是今天的重点,今天的重点在于把高斯分布变形,得到另一种表达的高斯分布,从而说明问题。
大家都在等待着概率论的登场
Canonical Caussian Repersentation
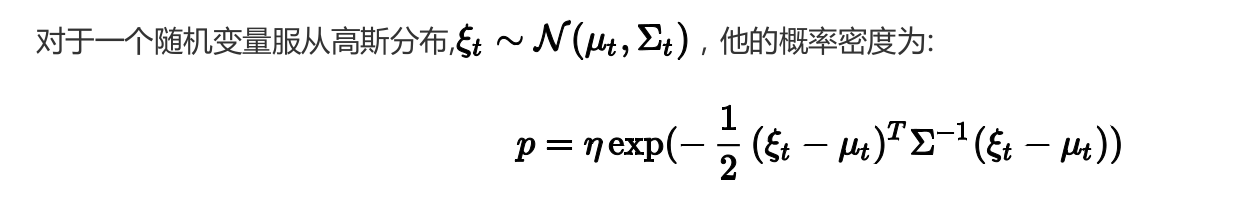
稍作变形有:
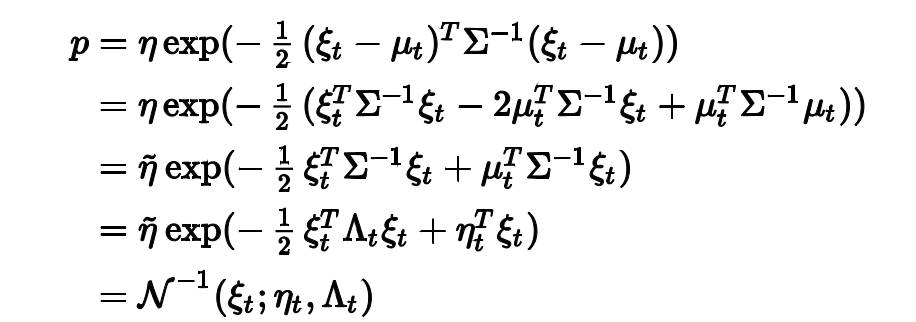
我们吧这种形式表达的高斯分布叫做Canonical form,其中Lambda叫做信息矩阵,eta叫做信息向量,这个形式的高斯分布和标准形式的高斯分布是一个对偶的关系,对于边缘概率和条件概率的计算,Canonical form边缘概率计算复杂(使用舒尔补,黄老师带你飞第二章部分内容),条件概率简单,standard form边缘概率计算简单,条件概率计算复杂,如下表:
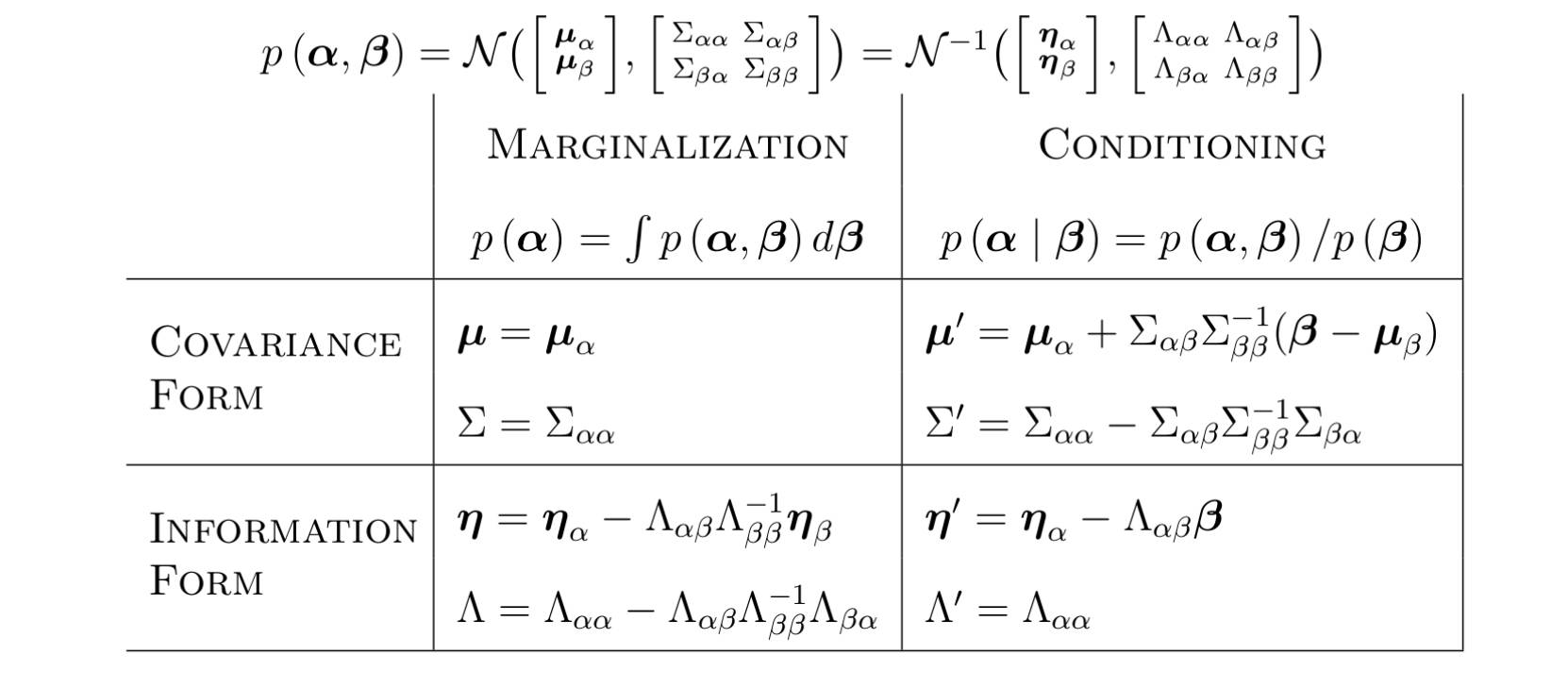
Encoding Markov Random Field
我们把刚刚那个信息矩阵形式(Canonical form)的高斯分布拿过来用一下(把中间的二次型写开来),可以得到这样形式的一个概率:
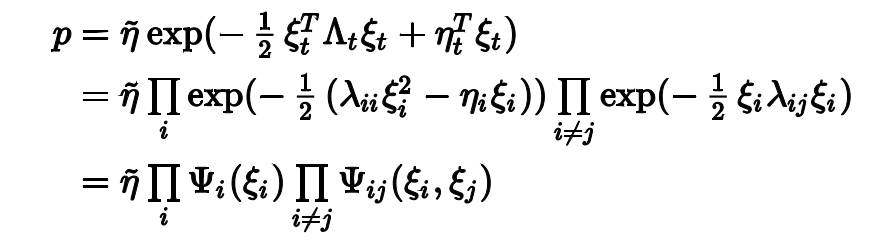
小伙伴们,你们知道这是啥吗?这就是传说中的因子图啊,概率分成了一元项和二元项,一元项表示节点(NODE),二元项表示边(EDGE),不相关的时候lambda_{ij}=0,那么正好二元项等于1,在乘法中就是乘了白乘,在图中正好不连这条边,而相关的时候,相关得越厉害,那个边就越强。
接下来,我们上一个图
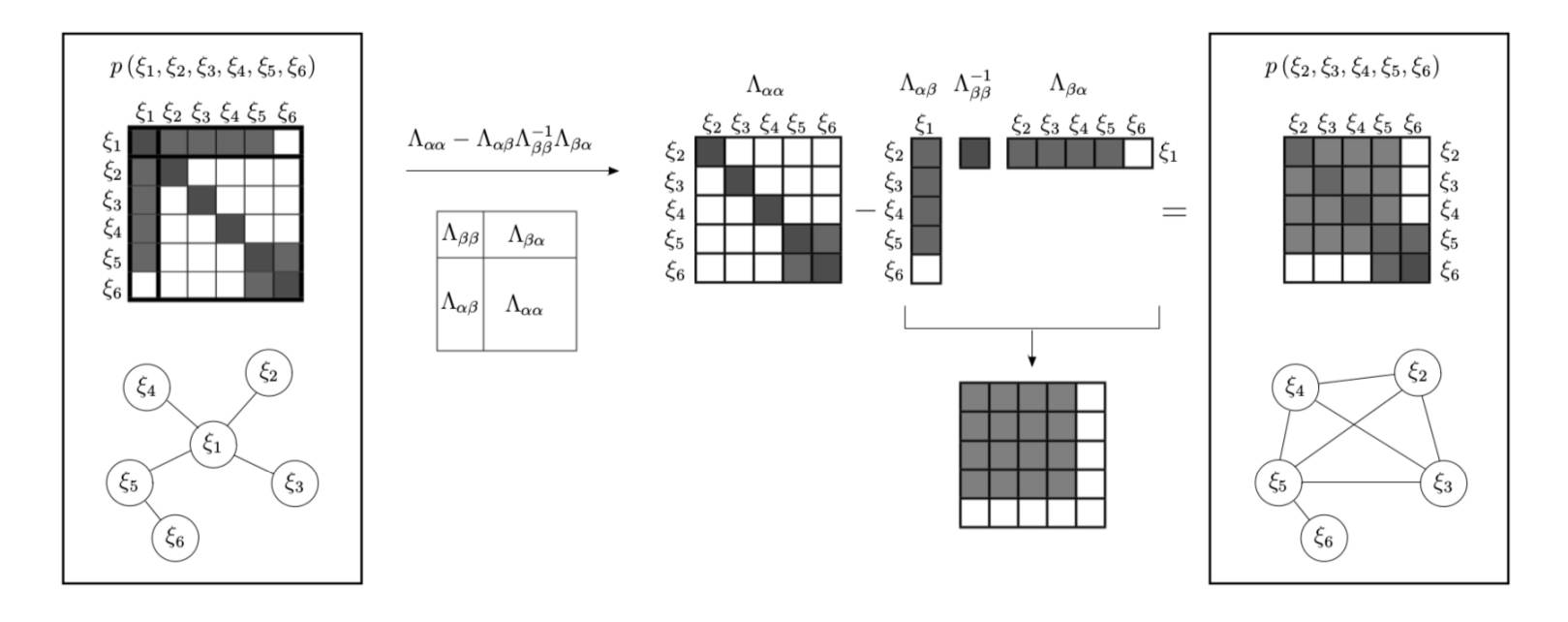
这个图是算边缘概率的图,注意到信息矩阵和图是一一对应的(最坐标那个框),然后中间的操作是算边缘概率的操作,注意看前面那个表,你会发现,marg过程中减号右边那一项,一个列乘以一行,得到了一个非常dense的矩阵,marg之后的矩阵就这样愉快地变得稠密了起来。
回到slam问题上
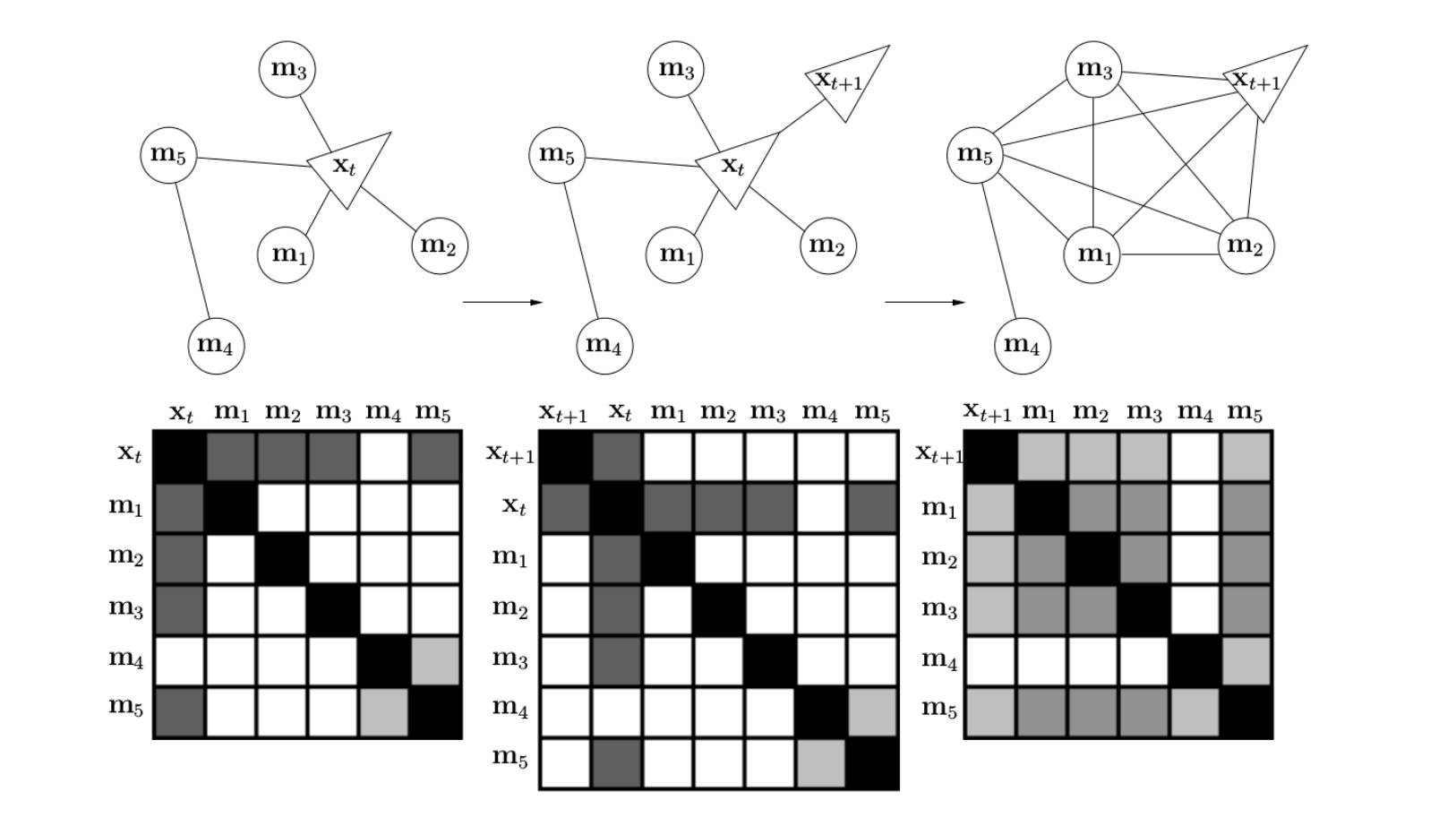
到了现在,我想你就能很清楚的认识到,为啥信息矩阵变得这么稠密了,如图所示,假如上一帧(左一),是这样简单的一个连接关系,然后在滤波的过程中,我们计算了联合概率(中),最后呢,是不是还要算边缘概率,这就得到了最右边的那个很稠密的信息矩阵了。你会发现,在运动的不断进行过程中,信息矩阵会越来越稠密,这是一个很大的问题。
大家都知道,最近的slam算法都喜欢玩sliding window,这个算法好在哪里呢?就是在计算过程中,吧前面的信息都保留了,这和BA有着很大的区别,我们做BA的时候,就直接认为地图点之间是没有连接的,帧与帧之间也没有什么连接,这其实是没有使用先验信息的处理方式,但是他对slam问题的稀疏性有很强的保证,但是sliding window呢?
sliding window有个marg过程,其实整个窗里面维护了一个hessian矩阵(信息矩阵),这个矩阵在marg过程中,会稠密化,最终会影响整个系统的效率,甚至导致系统崩溃。
在dso或者okvis中,其实都做了稀疏化处理,使得矩阵的稀疏化保持了下来,相关部分大家可以读相关论文,在信息滤波方法中,也有稀疏化策略,可以供大家参考。
祝大家新年快乐!
【版权声明】泡泡机器人SLAM的所有文章全部由泡泡机器人的成员花费大量心血制作而成的原创内容,希望大家珍惜我们的劳动成果,转载请务必注明出自【泡泡机器人SLAM】微信公众号,否则侵权必究!同时,我们也欢迎各位转载到自己的朋友圈,让更多的人能进入到SLAM这个领域中,让我们共同为推进中国的SLAM事业而努力!
【注】商业转载请联系刘富强([email protected])进行授权。普通个人转载,请保留版权声明,并且在文章下方放上“泡泡机器人SLAM”微信公众账号的二维码即可。






