专栏名称: 算法与数学之美

从生活中挖掘数学之美，在实践中体验算法之奇，魅力旅程，从此开始！

数学与大脑

算法与数学之美 · 公众号 · 算法 · 2017-03-16 23:54

正文

数学与大脑

来源：第九阅览室

编辑：Gemini

一个常人的脑体积约为1400立方厘米，重量约为鼠脑的1000倍。不过这一简单数据对了解大脑这个迷人的器官用处不大。人脑里装的东西令人赞叹：它能指导口头和书面语言、艺术与音乐创作以及数学研究。有没有这个可能：海豚已经解决了黎曼猜想，但我们因为还没能找到与之交流的方式而不知道这一点？
数学和大脑这个话题好像没有什么好谈的。然而，关于这个学科，当今已有了很多有意义的事情。本文将就这一话题抛砖引玉式地做些介绍。

想象大脑

长期以来大脑被视为神秘的理由是它位于脑壳之内，人们在通常情况下难以看见它。当伦琴(Wilhelm Roentgen)发现X-射线后，人们可以见到人类身体内部可是个大飞跃。就在发现X-射线后不久，医生就可以通过X-射线看到我们的骨头。但是，置于脑壳内的大脑以及其他一些软组织对于医生和生理学家而言依然是未开垦的处女地。随着科学、工程和数学的贡献，医生们已经有了不断增加的造影工具来看到脑壳内的东西。起初这些脑部造影技术涉及到大脑的二维截面。许多这些技术都与层面X光照相术有关。表示“切”或“截面”的希腊词是“tomas”。当层面X光照相术变得成熟后，已有可能产生大脑的三维截面医学造影系统，这些系统不但能观察脑子的静态状况，还能制作电影以显示大脑的动态行为。医学实践者和研究者现在可以用到的系统有：

CT或CAT（计算机层面X光照相术或计算机轴向层面X光照相术）
MRI（核磁共振造影）
fMRI（官能核磁共振造影）
PET（正电子发射层面X光照相术）
SPECT（单光子发射计算机层面X光照相术）
DOT（扩散光学层面X光照相术）

这样一些影像的“香草”样本如下列出：

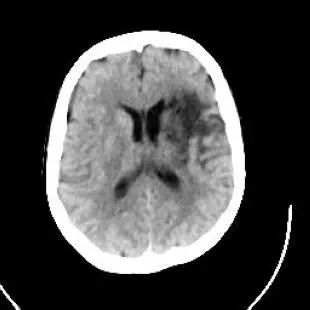
大脑的CT图像

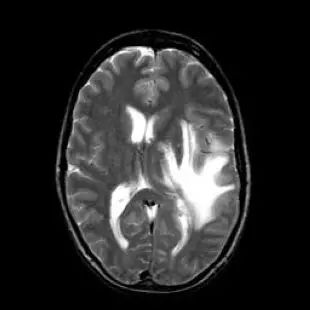
大脑的磁共振图像

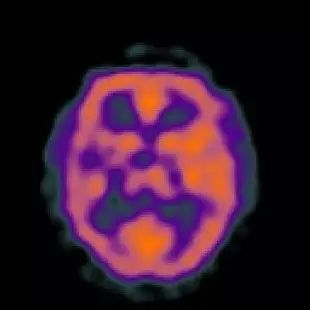
SPECT/PET大脑的图像

如上显示的影像已经成为我们社会专业词汇的一部分，医生可以根据图像信息发表意见并诊断疾病。

CT-扫描、计算机层面X光照相术的发展是诊断医学和医学研究的巨大进步之一。它也是纯粹数学、应用数学及计算机科学相互影响的一个绝妙的故事。

这个令人赞叹的故事从捷克开始。数学家拉东(Johnann Radon,1887-1956)当时在探索重建函数值的一个想法：函数在平面定义域中某一点处的值可以通过将它在与定义域相交的一些线段上的值求和（积分）而得到。这项研究于1917年以德文发表，拉东的工作演化成今日所称的拉东变换。

不清楚拉东是否预见到他的工作未来在医学上引起的革命，但不管怎么说，工程及计算机科学中将他的想法付诸实践是在很久的未来。半个多世纪后，他的思想被进一步放大，使得实用的层面X光照相术成为现实。

下面简介一下拉东的想法：考虑如下的例子，它是拉东所研究的方程的一个离散类似物。

图中“方形头”顶点的密度是未知的，由

x,y,z,w

表示。如果知道这些未知值在连接正方形顶点的6条线段中的某些（或全部）上的和，我们能重建这些未知密度吗？

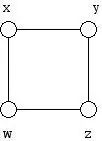
例如，用6条线中的4条，假设我们有方程

x+y=8,

w+z=10,

y+z=13,

w+y=7.

懂得一些线性代数的读者或许想知道一般情形下能看到什么。学过高中代数的读者应当能知道上述方程组有唯一的解。

含有四个未知数的四个方程通常有唯一解。但是，6个方程可能是不相容的，因而无解；或其解随着6个方程中选出4个的方式而定，但这时解就不唯一了。这类问题属于新生领域“离散层面X光照相术”。这些问题（上面的问题涉及二维立方体）属于从部分知识（或不同种类的样本）重建信息的一个领域。

拉东证明未知密度可以通过他所计算的“线积分”而重建。不清楚那时他或其他人是否已认识到这项工作对医学造影的价值，但如前所述，没有计算机的重要应用，拉东的工作不可能立刻就能应用。

CT-扫描的故事到了现代时光与Godfrey Hounsfield(1919-2004)和Allan Cormark(1924-1998)的工作相关。前者是一个英国电气和机械工程师，而后者则是南非的一个物理学家。这两人由于他们的工作共享了1979年的诺贝尔生理与医学奖。然而，1971年开发出的扫描仪（基于其他想法）的最初操作却与拉东的工作无关。罗格斯大学的数学家Larry Shepp听了Hounsfield的一个演讲，这个演讲描述了他的新器件。Shepp一下子看出Hounsfield并不知道拉东的研究结果和其新机器相结合的可能性，故他介入其中，开发计算机程序，以改善新技术的成像质量。

随着时间的推移，越来越多的数学家们投身到多种类的造影技术。

人类视觉系统

连接数学与大脑的一个丰硕的领域是视觉现象。人的视觉信息由大脑处理，大脑再启动我们神奇的眼睛。数学家已经涉及到关于视觉的广泛问题：

我们的知觉系统的几何是什么？
大脑怎样处理视觉信息？

众所周知，当人们注视一条笔直的铁道时，铁道两边的轮廓在远处相聚一点。众多的学者试图理解视觉之谜。世界在我们眼中的方式对艺术家是挑战，他们必须在帆布上表示现实；对哲学家也是挑战，他们试图处理精神世界、物理及知觉之间的关系；艺术家以透视理论面对这种挑战，而数学家（他们当中有些也是艺术家）则通过透视得到的洞见转化成今日所称的射影几何。不像欧几里得几何，在射影几何中没有平行线。但这不是故事的终极。有建议说双曲几何或其他几何也可以描述这个系统。从数学的观点理解透视的挑战并能够用计算机为艺术家、摄影师和建筑师的需要服务，已经成为许多研究的源泉。

幻觉与不可能的图形

数学与大脑的一个有趣联系是许多人对对称模式和迷惑性（视觉幻觉和不可能图形）模式的反应。包括数学家在内的许多人发现对称设计非常吸引他们。例如，M.C. Escher(1898-1972)的作品在数学家的团体中得到许多共鸣。

更进一步，在Escher与光学幻觉的兴趣和“不可能物体”之间有一种联系。这种关联来自杰出的数学家和物理学家彭罗斯(Roger Penrose,1931-)，他的不可能三角形已经激起了包括Escher在内的大量艺术追求，以及数学、计算机方面的视觉探索。

然而，并不广为人知的是，彭罗斯并非是创造这些图形的第一人，但是他的幻觉版本是特别吸引人的。

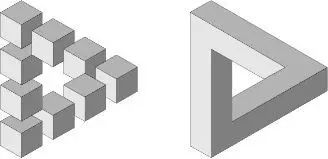
上图右边的是属于彭罗斯的版本，但左边的同一物体的说明版本则在1934年由瑞典艺术家Oscar Reutsvǎrd首创。Reutsvǎrd的作品已被瑞典邮票纪念发行，且他的不可能三角形版本只是他创造的众多幻觉物体之一。后来发现，“不可能图形”的另一方面是使得一些真实物体看上去就像是不可能的东西。幻觉具有比到达眼睛或大脑更多的东西。

幻觉开启了探索我们视觉系统的本质、大脑处理视觉信息的方式以及我们的视觉知觉系统的几何的一扇窗子。计算机视觉是一门学科，它包括处理计算机图像的有效方式以及开发用于各种各样模式识别问题的软件。该领域的专家们也对视觉幻觉感兴趣。这个领域研究成果的应用包括更有效的面部识别到情景识别能力等等。下面有少量的视觉幻觉样本，它们显示可以探讨的一些现象，例如关于大脑为何可被“愚弄”，也许可以通过数学建模。

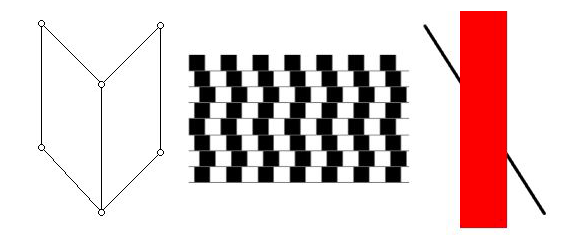
上述的几个小样本当然不能给出这两个学科之间的无数联系。下面再列出一些数学与大脑相互影响的例子：其他关于大脑的数学

神经原组织及大脑与我们的其他神经系统之间的信号传输（神经传导）。
运用动力系统来试图理解癫痫以及能够预测疾病的起始。
用数学为大脑的不同方面建立模型，试图理解“振动器”在不同相互作用假设下怎样协调它们的第一线工作。
运用将（像大脑这样的）复杂表面平展化的新想法以便理解大脑不同部位怎样行使特定的脑功能。
利用数据挖掘及其他工具以理解不断增加的来自脑化学的DNA和基因信息的用途。

数学能力

就我们最大限度的所知，人类是唯一能做数学的生物体。任何证实其他动物或植物能“做”数学的试图至今都未能得到证实。“聪明的汉斯”中有一匹名为汉斯的马让其主人相信它能做数学的著名故事，但这并不是因为这匹马有什么数学才能，而是主人自己不经意地给马发出的信号所然。人类大脑具有做数学能力的原因到底是什么？大脑造影技术正被用来图示人类在进行计算、视觉化多面体、试图证明定理、或猛攻数论难题等方面的不同之处。具有“强记忆力”的人通过什么方式使得数学研究较易？许多数学家把自己说成记忆力超强的人，这对研究数学有用吗？总而言之，数学家们正利用他们的大脑和数学不断推进数学领域，并试图更进一步地给出大脑的超凡结构的真知灼见。

往期经典文章回顾