翻译/编辑/部分原创 Vivian Ouyang  原作者：Sunil Ray     数据圈资深成员

作者简介：美国达拉斯一家医院数据中心工作，职位是data scientist。主要做healthcare方面的数据分析建模

在机器学习中，很多时候你会挣扎于怎么提高模型的准确率。在这种时刻，数据探索的一些方法将帮助你解决这个问题。这个指导将帮助你理解数据探索中的主要技术。请记住你输入的变量的数据质量决定了你模型输出量的质量。所以当你的商业问题提出来以后,你需要花费很多时间在数据准备和探究上面，一般来说，数据清理，探究和准备大概占据了一个项目70%的时间。下面是准备，理解，清理你用于建立预测模型的数据的几个步骤,我会一个一个来介绍

1.变量确定

2.单变量分析

3.双变量分析

4.处理缺失值

5.处理离群值

6.变量转换

7.变量创建

首先上部会介绍1,2,3,4四个部分。

变量确定

首先，你需要确认你的输入变量（预测指标）和你的输出变量（目标变量）是什么，接着，你需要确认数据的种类和分类。下面用一个简单的例子来说明，假设现在我们想要预测学生是否玩板球（cricket），现在我们需要确定输入变量，输出目标变量，以及每一个变量的分类和种类，下面是部分原数据

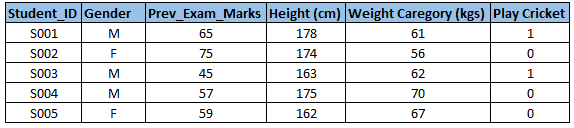
Student_ID:学生编号

Gender:性别（F-女，M-男）

Pre_EXAM_Marks:之前的考试分数

Height(cm):身高（厘米）

WeightCaregory(kgs):体重（千克）

Play Cricket:玩板球（1：玩板球，0：不玩板球）

下面这个图是以上变量的分类和种类图

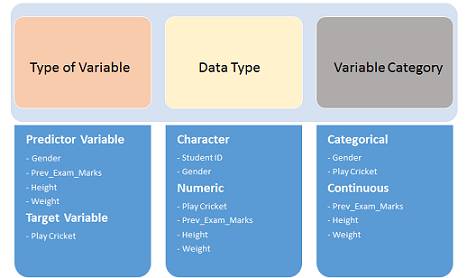
从上图可以看到，输入变量（预测变量Predictor）是性别，之前的考试分数，身高，体重。而输出值（目标变量Target）是是否玩板球。学生编号和性别是字符变量(Character),是否玩板球，之前的考试分数，身高，体重是数字变量（Numeric）。从连续和非连续来分类的话，性别和是否玩板球是非连续变量（Categorical），之前考试的分数，身高和体重是连续变量（Continuous）

单变量分析

在这个步骤，我们需要一个变量一个变量的去做分析，单变量分析的方法取决于你需要分析的变量是连续的还是非连续的。

连续型变量（Continuous Variable）：对于连续型变量我们需要知道这个变量的中心（central tendency）和展布（spread or dispersion），下面是描述变量中心还有展布的指标量，以及用什么图来进行可视化。

中心：平均值，中位数，众数，最小值，最大值

展布分布：范围，四分位数，内距（四分位距），方差，标准差，偏态与峰度

可视化方法：直方图（最右的图），箱线图（中间一个图）

非连续型变量（Categorical Variable）：对于非连续型变量，我们使用频率表来显示每一个分类的分布，同时我们也可以计算每一个分类的百分比。一般可以使用条形图或者箱线图来可视化

双变量分析

双变量分析是用来找出两个变量之间的关系，我们寻找两个变量间有显著水平的相关联和非相关联性。双变量分析可以是非连续型变量和非连续型变量，非连续型变量和连续型变量还有连续型变量和连续型变量。下面我们将一个一个情形来说明。

连续型变量和连续型变量：对于两个连续型变量，一般可视化我们使用散点图。散点图很好的显示了两个变量的关系，这个关系可以是线性也可以是非线性的。

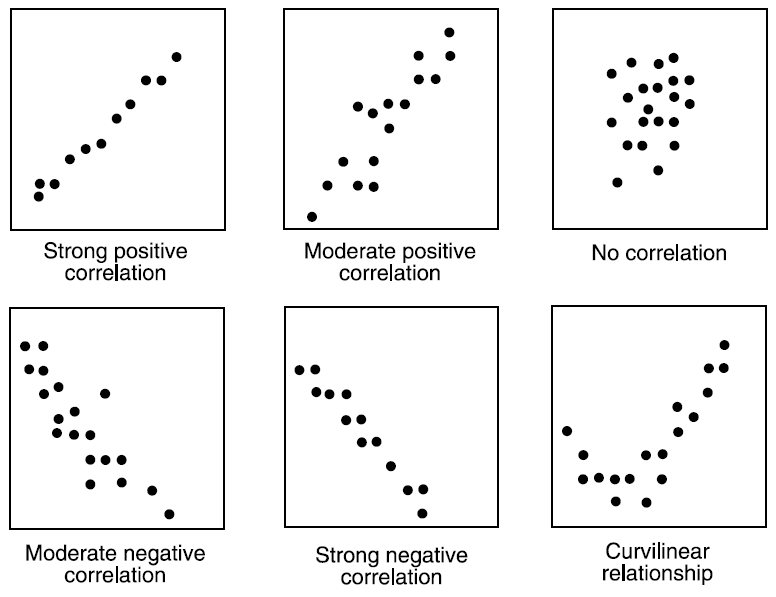
上面的六个图，左上是很强的正相关，意思是指当其中一个变量增加时，另外一个变量增加，上面正中间的是中等强的正相关，右上是没有相关性，左下是中等强的负相关，意思是指当其中一个变量增加时，另外一个变量减少，下面正中间是很强的负相关，右下是非线性的相关。一般散点图只是显示了两连续变量之间的关系，但是并没有显示关系的强度大小。所以我们使用一个指标相关（Correlation）来显示关系强度的大小，相关的大小可以从-1到+1。其中“-1”指的是完美的负线性相关，“+1”指的是完美的正线性相关，“0”指的是没有线性相关（但是可能有非线性的关系）。计算相关的公式如下

相关=变量X和Y的协方差/变量X的方差和变量Y的方差乘积的平方根

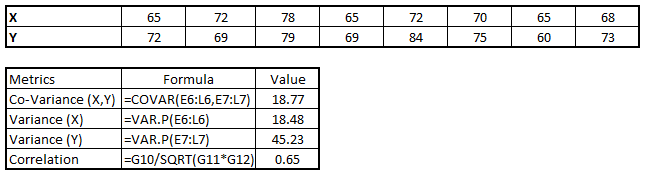
如果使用Excel，可以用CORREL（）来计算两个变量的相关。如果使用SAS可以使用PROC CORR来计算相关，如果用R，可以使用cor.test（）来计算相关。如果用Python,可以使用numpy.corrcoef（）来计算。下面是用EXCEL计算相关的例子，X和Y的相关系数是0.65。

非连续变量和非连续型变量：

双向表（two-way table）:我们可以用一个双向表来分析两个非连续变量的关系，双向表的行代表一个非线性变量的分类，列代表另一个非线性变量的分量，然后每个小格（cell）可以显示数目还有所占的百分比（双向表是下面最左边的表）。

堆积柱图（Stacked Column Chart）：这个其实就是双向表的可视化（上面右边两个表）

卡方检验（Chi-square Test）：这个检验是用来检验变量关系的显著性。主要是比较两个及两个以上样本率( 构成比）以及两个分类变量的关联性分析。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。它会反馈用卡方分布计算的p值，当p=0的时候，这两个变量是相互依赖的（dependent），当p=1的时候，可以理解为这两个变量独立(independent)，当p值小于0.05的时候，意味着有95%的信心这两个变量的依赖性是显著的。卡方检验的统计量是

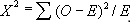
其中O表示实际观察到的频数，而E表示当这两个变量独立的时候，双向表中每个cell的理论频数。

非连续变量和连续型变量：

对于探索连续变量和非连续变量的关系，对于可视化，我们可以画非连续变量每一个分类的箱线图（boxplot）。而如果想用统计方法来检验它们之间的关系是否显著，可以使用Z检验，t检验或者方差分析（ANOVA）。一般Z检验用于样本比较大的情况，检验的是两组之间的均值是否有显著不同。t检验一般用于样本比较小的情况（每一组都小于30），检验的也是两组之间均值是否有显著不同。而ANOVA是用来检验多于两组的时候， 多个组的均值是否有不同。

缺失值处理

在数据清理中，我们经常会遇到很差的数据，会有很多缺失值，如果训练数据中有缺失值的话会让训练出来的模型有偏差或者不够拟合数据。缺失值出现的原因也有很多种，它们一般出现在两个阶段

数据抓取：在抓取数据过程中，因为没有符合抓取的指导或者要求，而造成的一种缺失，这种缺失比较容易被发现并且很快的改正

数据收集：在数据收集阶段的缺失比较难改正，因为有大概四种不同的情况

完全随机缺失(Missing Completely at Random)：这种情况是指对每一个观测值，缺失的概率是一样的。打个比方，比如现在需要一群人上报自己的收入，对于每一个上报者，在上报之前先丢硬币，如果是正面就上报收入，如果是反面就隐瞒收入。因此对每个观测值都有一半的机会缺失或者不缺失。

随机缺失（Missing at Random）：随机缺失是指缺失值是任意缺失的但是对不同的输入变量和分组，缺失值的比例是不同的。比如当我们想收集女性的年龄时，女性比起男性会有更多的缺失值（很好理解，女性一般不太喜欢被访问年龄）。

缺失依赖于未观测到的自变量 （Missing that depends on unobserved predictors）：

当缺失值不是任意随机的，而是和某些我们没有观测到的值有关。打个比方，比如在医药研究中，如果一种治疗方法引起了病人身体的不适应，那么病人有很大的概率会提前从这个研究中退出导致最后他/她的观测值是缺失的，这种缺失不是任意的而是和身体不适应相关的。

缺失值依赖于缺失值本身 （Missing that depends o the missing value itself）：

当缺失的概率直接和缺失值本身有关的时候。比如，一般很高收入和很低收入的人不太喜欢被访问收入多少，因此收入会有缺失值。

处理缺失值的方法

a. 删除：表删除（List-wise Deletion）和对删除(Pair-wise)

通常的数据表中，行代表样本，列代表不同的变量。在列表删除中，只要一行有任何一个变量的值有缺失，我们就删除一整行的信息。简单是这个方法的主要优势，但是很大的劣势也是这样严格的删除会导致样本量的减少。在成对删除中，我们对每一个变量就用它不缺失的样本数进行逐个分析，这种方法尽量的保留了样本个数，但是不好的是对每一个变量你所使用的样本个数也不一样。两种删除方法如下图例子所示，左边是表删除，而右边是对删除，你可以看到左下图任何一行有缺失就会被划掉删除，而右下表，对性别（gender），劳动力（manpower），销售（sales）变量每一个分别删除缺失值，而不是一行全部划掉。

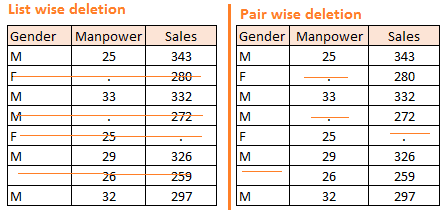
主要备注：删除的方法只能用于完全随机缺失(Missing Completely at Random)的情况，随意删除不随机的缺失值会使数据产生bias。

b. 均值（mean）/众数(mode)/中位数(median)替换法

替换法是用估计的值去替换缺失值的方法。这个方法的目的是利用已知的可以定义的不缺失的数据去帮助估计缺失的数据。均值/众数/中位数这三个都是经常被广泛使用的方法。这种替换法一般也有两大类：

第一种就是一半的替换，就是我们计算缺失的变量剩下不缺失的数据的均值，众数或者中位数来替换缺失值。例如上图那个例子，对劳动力那一个变量的缺失值，我们计算不缺失的劳动力的数据得到28.33，然后用这个值来替换缺失值。

第二种就是相似替换，比如在上图那个例子里的劳动力，我们分别计算不缺失的男和女的劳动力平均值，分别是男29.75而女25，因此对于男，缺失的劳动力就用29.5替代，而对于女，缺失的劳动力就用25替代。

c.预测模型

用预测模型来估算缺失值也是一种理论比较成熟的方法。一般我们会把数据集分为两个部分，一个部分完全没有缺失值，而另一个部分含有缺失值。没有缺失值的数据集作为我们的训练数据集来得到预测模型，而有缺失值的数据集作为检验数据集，而缺失的变量就作为要预测的目标输出量。下一步，我们用训练集生成一个预测模型，用其他的变量来预测缺失的变量，然后把预测模型用到检验数据集来得到缺失部分的预测值。我们可以使用回归，方差分析，逻辑回归或者其他的机器学习的方法去做预测模型。

不过这个方法也有明显的缺点，如果缺失的变量与其他的变量没有什么关系，这个预测将会不准确。

d. 最近邻居法（KNN）

在这个替换方法中，我们用缺失值周围的离它最近或者是最相似的其他变量来估算。一般两个变量的相似度是有距离来决定的。距离的定义可以有多种。这个方法的优点就是缺失值是连续的或者非连续的变量都可以替换。不需要对每一个缺失的变量生成预测模型。数据变量间的关系也都被考虑进去了。而缺点是对于很大的数据集，这个方法很耗时，因为它会搜索所有的相似变量，而且k值的选择（就是缺失值周围选k个点）也是很重要的，高的k值会让几乎和缺失变量不相关的变量包含进来，而低的k值都会把很相关的变量可能排除出去。

在机器学习中，很多时候你会挣扎于怎么提高模型的准确率。在这种时刻，数据探索的一些方法将帮助你解决这个问题。这个指导将帮助你理解数据探索中的主要技术。请记住你输入的变量的数据质量决定了你模型输出量的质量。所以当你的商业问题提出来以后,你需要花费很多时间在数据准备和探究上面，一般来说，数据清理，探究和准备大概占据了一个项目70%的时间。下面是准备，理解，清理你用于建立预测模型的数据的几个步骤,我会一个一个来介绍

1.变量确定

2.单变量分析

3.双变量分析

4.处理缺失值

5.处理离群值

6.变量转换

7.变量创建

在下部会介绍5,6,7三个部分。

处理离群值

离群值（Outlier）经常会引起很多错误的模型估算和预测。简单的讲，离群值就是离整体数据分布或者模式很远的观测点。举个简单的例子，一个研究显示一般人的年收入是8万，但是发现其中有两个用户的年收入有4块钱或者400百万，这两个用户就可以看成是离群点。下图就是一个箱线图的离群点的例子，被圈出来的就是离群点。

离群值的种类

离群值一般有两个种类，一个是一元离群值，一个是多元的离群值。比如上面箱线图的离群值点。这种离群值一般是在我们观察单变量的分布的时候。 而多元离群值是指多维的空间，如果想找到他们，你必须看数据点的多维分布。让我们用身高和体重之间的关系来理解一元和多元离群值。如下图，左下和左中分别是身高和体重分别的箱线图，我们并没有看到离群值，而当我们画出右下图的身高体重散点图的时候，我们发现了三个离群值。

知道了离群值的分类，每次当我们遇到离群值的时候，最好的办法就是找到为什么这些值会离群。离群值产生的原因也可以分为两大类

假的离群（就是误差）/非自然的离群：

1.输入误差：就是在数据收集中产生的人为的错误，比如数据记录，数据输入错误都会引起离群值。打个比方，一个顾客的年收入有十万元，而数据输入员将它输入成了100万元，是原来的十倍。这个就会造成离群点。

2.测量误差：这是最常见的离群值的来源，这个一般是由测量仪器的错误造成的。比如，你有十个测量仪器，其中9个是准确的一个是坏的。那么被坏仪器测量的组将会比其他仪器测量的组高或者低一些。这样会引起离群点。

3.故意的离群值：这个经常发生在一些有敏感数据的自我报告中。打个比方，比如青少年一般会少报他们一周喝酒的数量，只有很少的一部分青少年会如实汇报。那么因为大部分人都少报，那实际汇报的那些数据反而看起来像离群点了。

4. 数据处理误差：当我们做数据分析的时候，我们会从不同的平台抓取数据，那么这些抓取和转换回来带一些误差，从而产生离群值。

5. 样本误差：很简单的比方，比如我们要测量一般运动员的身高，但是我们不小心把几个篮球队员算进去了，因此这些造成了离群值。

自然离群

当一个离群值不是因为误差引起的，那么就是自然离群值，比如，有时候在比赛中，前面五十名比后面的几百个人好太多，那一般不是因为误差，因为离群值很多，那这种情况，就属于自然离群，我们需要单独对待这一部分人。

离群值的影响

离群值会很明显的改变数据分析与建模的结果，他们有很多的不好的影响

1.它们会增加误差的方差，而一般误差的方差平方根会作为统计量的分母，因为减小统计量的大小，造成p值变大，从而降低模型的统计功效。

2.如果离群值是非随机分布的，那么它们会影响数据正态性分布。而很多线性模型的假设就是输出变量Y是正态分布。

3.离群值还会影响估计值，让其差生偏差

4.离群值也会影响很多统计方法的统计假设比如线性回归，方差分析。

为了容易理解，我们看一个简单的例子，如下图

在右上图，因为有了离群值300，而导致标准差，均值什么的都产生了很大变化。这会完全改变你的统计估计。

离检验离群值

绝大多数探测离群值的方法都是可视化数据，我们使用不同的可视化方法，比如箱线图，频率图，散点图。当然也有一些简单判断的准则。比如对于一元离群值，对于任意的数据，一般的范围是正负1.5倍的四分卫距（IQR）这种。而二元或多元离群值一般是用一种距离计算来判断，比如马氏距离或者线性回归中的Cook距离。

移除离群值

绝大多数处理离群值的方法与缺失值比较类似，可以删除或者转换，或者替换。

删除观测值： 如果是因为非自然的离群值，而且数量很少的话，我们可以移除它们。

转换以及给变量分组：转换变量可以减少离群值，比如给变量取自然对数。然后对变量进行分组也是个不错的转换方法。比如对于分组过的变量，决策树就可以很好地处理这些离群值。而且我们还可以给不同的观测值不同的权重。比如下图右边就是把左边的观测值进行了取自然对数过后得到的新观测值。

替换： 类似于缺失值的替换，我们也可以替换离群值，可以使用均值，中位数，众数等方法。如果是非自然的离群值，我们可以用统计方法去预测离群值。

单独处理: 与缺失值处理不同以及增加的一项，就是单独处理了。如果离群值数量很多，我们在统计建模中，应该把它们单独作为一组单独分析。一般来说比较流行的统计方法，有那种对不同的组分别建模然后给权重进行联合的方法。

变量变换

现在让我们跳到数据探索的最后一个阶段：特征工程。在介绍6.变量变换和7.变量创建时，先介绍一下特征工程，因为6和7是特征工程很重要的组成部分。特征工程是建模中很重要的一步，是怎么从已有的数据中提取更有用信息的艺术。你并不添加任何数据，而是让你现有的数据怎么变得更加有用。一般特征工程的前五步就是我之前介绍的1，2，3，4，5.而后面两步就是变量变换和变量创建。这两步对你模型的预测准确度有很大的影响。

在数据建模中，变量变换是指一个变量用其相关的函数变换之后的值来表示。打个比方，我们用x取对数之后的值来取代x的值。也可以说，变量变换改变了变量的分布。那什么时候我们需要使用变量变换呢。下面是四种情况：

1.当我们想要改变一个变量的scale活着标准化它想让这个变量的变得更容易理解。如果你的数据有不同的scales，这种改变并不改变变量的分布的形状

2.当我们想要把变量之间非线性的关系变成线性的。一般来讲，线性关系比非线性的关系容易让人理解。变量变量可以帮助我们完成这个。一般散点图可以让我们可视化两个连续变量之间的关系。比如取对数变换是我们经常用的方法。

3. 比起倾斜分布的变量，我们更喜欢对称分布的变量。对称分布的变量比较容易解释而且也易于用于参数估计。比如一般线性回归会要求误差服从正态分布，这里的正太分布就是对称分布的一种。对于参数模型，我们一般都有变量的分布假设，而很多时候，我们都假设变量是对称分布，模型的理论推导也是建于对称分布而来的。因此每当你有遇到很倾斜的分布的时候，最好对变量做一些变换。比如，对于向右倾斜的分布，我们可以去平方根或者立方根，也可以去对数。而对于向左倾斜的分布，我们可以平方，或者立方或者指数化我们的变量。比如右下图向右倾斜的分布我们就指数化我们的变量

4. 有时候变量变换是来自于项目的要求，或者说能更好的完成项目的任务。打个比方，在某个人力资源的分析中，我们发现，年龄和员工的表现有很大的关系。年龄越大，表现越好。从应用的观点来看，一般更喜欢把年龄分层成比如<30岁，30-45岁，>45岁，然后对每一组年龄层，采用不同的策略。这种方法就叫做变量分层（binning)

知道什么时候做变量变换了，那有哪些变量变换的基本方法呢

取对数：一般用于向右倾斜分布的变量，但是它不能用于0或者负值

平方根/立方根：平方根或者立方根变量也可以改变变量分布，不过不如取对数明显。但是立方根有自己的优势，它可以用于0值还有负值。平方根变量可以用于含0的正值。

分组（binning）：这个适用于分组变量，很多时候这种分组是建立于商业理解上。比如我们会把收入分为高收入，中等收入和低收入。当然我们有两个变量还可以一起做多元分组。

变量建立

变量建立是利用原有的变量创建新变量的过程。打个比方，我们有日期的输入变量（日-月-年），我们可以利用这个变量建立专门的日，月，年，星期，工作日等等比之前的输入变量日期更好的变量。这个方法有时候用来强调变量的一些隐藏信息和关系。下面这个表就是把日期（date）变成三个新的变量（New_Day,New_Month,New_Year)的例子。

当然创建变量有很多方法，下面就介绍其中的两种：

创建派生的变量：

这个是从原有的变量中通过函数或者其他的方法得到新的派生变量。比如kaggle竞赛中很有名的泰坦尼克号数据，很多参赛者会喜欢从人的名字变量中创建Master，Mr，Mrs和Miss这四个新变量。那一般怎么决定派生变量呢。大部分时候要按你的商业要求来。

创建虚拟的变量：

还有一个普遍的情况就是创建所谓的虚拟变量，一般用虚拟变量把非线性的变量变成数值变量。虚拟变量又叫指标变量。比如对于性别（gender）有男和女两种，那么我们可以建立两个新的变量一个叫Var_Male，它的值为 1（男）和0（女），然后Var_Female变量，它的值为 0（男）和1（女）。如果非连续变量有n层（大于2），那么可以创建n-1个虚拟变量。下面这个图就是用性别变量（gender）来创建两个虚拟变量（dummy variable）。

数据探索就介绍完了。总之，任何时候都不要小看data exploration，它是你建立模型的第一步。

关注我就是关注你的未来，后续还有系列文章

目前已有550+位行业人士加入.......