编者按:UCLA以电路方向的研究和教学闻名于世界,Behzad Razavi教授和Asad Abidi教授更是世界闻名的电路大师。UCLA的研究生课程模拟集成电路设计(EE215A)正是由Razavi和Abidi两位大师轮流授课。我有幸在UCLA上过两位大师的课,在这里想和大家分享课程的精华部分。两位大师上课的内容略有不同互为补充,所以我们的系列文章中部分笔记内容来自Razavi部分笔记内容来自Abidi。Razavi的EE215A讲义可以在他的主页找到(www.seas.ucla.edu/brweb/teaching.html),不过Razavi上课的风格是发一份讲义然后在关键部分留下空白需要学生自己作笔记以避免学生翘课☺。Abidi的EE215A笔记由卓伟汉整理。讲义的版权归两位教授所有。这是本课程的第二讲。
我们也准备了本次课程解说的pdf版下载,感兴趣的朋友请在关注矽说(微信号:silicon_talks)后发送消息“215A_pdf2”获取下载链接
(Abidi教授,用粉笔敲了几下黑板,双手叉腰说道:”Let’s resume!”)

在模拟集成电路设计第一讲
()
中,我们介绍了
LTI
系统。对于一个
LTI
系统,可以定义系统冲激响应的拉普拉斯变换
H(s)
为
传输函数
,使得对于变包络正弦激励
x(t)=e
st
, LTI
系统的响应为
y(t)=H(s)e
st
。那么问题来了,我们系统的输入激励可以是任意波形(方波,三角波等等),如何在对任意输入激励使用传输函数呢?这时候我们就需要神奇的拉普拉斯变换。根据拉普拉斯变换的卷积性质:
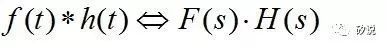
其中
“*”
表示卷积运算。同时,对于
LTI
系统,对于输入激励
f(t)
的响应
y(t)
正是
f(t)
与系统冲激响应
h(t)
的卷积。因此,系统响应
y(t)
的拉普拉斯变换
Y(s)
正是输入激励的拉普拉斯变换
F(s)
和系统冲激响应的拉普拉斯变换(即系统传输函数)
H(s)
的乘积:
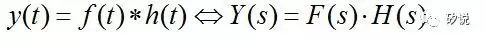
因此,我们可以很方便地在拉普拉斯域处理
LTI
系统,并且把得到的
Y(s)
做拉普拉斯反变换来得到系统的时域响应。更方便的是,当多个
LTI
系统级联在一起的时候,我们可以通过把多个系统的传输函数相乘来得到总的系统传输函数。

在线性电路分析中,最重要的一类
LTI
系统是二端口网络,因为大多数基本电路都可以用二端口网络来近似描述。二端口网络由传输函数矩阵来描述。举例来说,我们可以用
Z
参数(矩阵)来描述一个二端口网络:
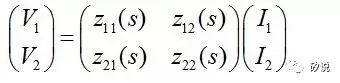
其中
V
1
,
V
2
分别是端口
1
和端口
2
的电压;
I
1
,
I
2
分别是流入端口
1
和端口
2
的电流。传输函数矩阵由
z
11
(s), z
12
(s), z
21
(s), z
22
(s)
组成,每一个
z
ij
(s)
都是一个传输函数。
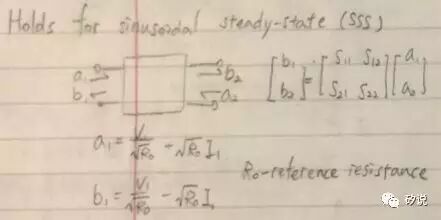
除了
z
参数之外,常用的二端口网络传输函数矩阵还包括
y
参数(
z
参数的对偶,输入为电压而输出为电流),混合参数(混合
=hybrid=h
,即
h
参数,输入包括电压和电流,输出也包括电压和电流),以及在射频微波电路中得到广泛应用的散射参数(散射
=scatter=s
,即
s
参数,输入和输出是在两个端口的入射
/
反射波幅度)。
(敲黑板:以上是对二端口网络的简单回顾,接下去要讲的二端口网络传输函数以及零极点的性质是这一讲的重点)

对于二端口网络传输函数矩阵中的任何一个传输函数
H(s)
,我们都可以写成如下形式
:

其中
a
0
, a
1
,…a
n
以及
b
0
,b
1
,…b
m
的值取决于网络的具体结构。

对于实际二端口网络,分子
p(s)
和分母
q(s)
的根是实数或者是共轭复数对。所以我们可以把
H(s)
写成















