神经网络是机器学习算法中最流行和最强大的一类。但在作者看来,因为人们对神经网络工作原理存在误解,导致网络设计也很糟糕。所以这篇文章就对其中一些误解进行了讨论。
神经网络是机器学习算法中最流行和最强大的一类。在计量金融中,神经网络常被用于时间序列预测、构建专用指标、算法交易、证券分类和信用风险建模。它们也被用于构建随机过程模型和价格衍生品。尽管神经网络有这些用处,但它们却往往有一个坏名声,因为它们的表现是「不可靠的」。在我看来,原因在于对神经网络工作原理存在误解,导致网络设计也很糟糕。本文将对其中的一些误解进行讨论。
核心要点
神经网络不是人类大脑的模型
神经网络并不是统计学的「弱形式」
神经网络流行许多不同的架构
规模很重要,但并不是越大越好
神经网络的训练算法有很多种
神经网络并不总是需要大量数据
神经网络不能基于任何数据训练
神经网络需要被再训练
神经网络不是黑箱
神经网络不难实现
1. 神经网络不是人类大脑的模型
人类大脑,是我们这个时代最大的奥秘之一,科学家还未对其工作方式达成共识。目前已有的关于大脑的两个理论分别叫做祖母细胞理论(grandmother cell theory)和分布式表征理论。前一个理论认为,单个神经元具有很高的信息容量,能够表征复杂的概念,如你的祖母或甚至 Jennifer Aniston(《老友记》女主角之一--译者)。后一个理论则认为,神经元要简单得多,而复杂的表征分布在许多神经元上。人工神经网络受到了第二种理论不够精确的启发。
我认为,目前这一代神经网络不具备感知(sentience,一个与智能不同概念)能力的一个原因在于,生物神经元远比人工神经元复杂。
大脑中的一个单个神经元就是一个极其复杂的机器,即使在今天,我们也还不能理解它。而神经网络中的一个「神经元」只是一个极其简单的数学函数,它只能获取生物神经元复杂性中极小的一部分。所以,如果要说神经网络模拟大脑,那也只在不够精确的启发水平上是对的,但事实上人工神经网络和生物大脑没什么相似之处。 --吴恩达
大脑和神经网络之间的另一个巨大不同:大小和组织性。人类大脑包含的神经元和突触数量远多于神经网络,而且它们是自组织和自适应的。相对地,神经网络是根据一个架构进行组织的。神经网络的「自组织」非常和大脑的自组织并不是一个意思,它更类似于一张图标,而不是一张有序的网络。
最先进的大脑成像技术生成的有趣大脑视图
所以,那是什么意思?可以这样想:神经网络受到大脑启发,就像北京的奥运体育场的设计灵感源自鸟巢。这并不意味着,该奥运体育场就是一个鸟巢,只是说,鸟巢的一些元素存在于该体育场的设计中。换句话说,大脑的元素存在于神经网络的设计中,但它们的相似程度比你想象的低得多。
事实上,比起人类大脑,神经网络更接近于曲线拟合(curve fitting)和回归分析(regression analysis)等统计方法。我认为,在计量金融的背景中记住这一点很重要,虽说某件事物是「由大脑启发的」可能听起来很酷,但是,这一表述可能会导致不切实际的期望或担忧。

曲线拟合,亦即函数逼近。神经网络常被用来逼近复杂的数学函数
2. 神经网络并不是统计学的「弱形式」
神经网络由互连节点层组成。单个节点被称为感知器(perceptron),类似于一个多元线性回归(multiple linear regression)。多元线性回归和感知器之间的不同之处在于:感知器将多元线性回归生成的信号馈送进可能线性也可能非线性的激活函数中。在多层感知器(MLP)中,感知器按层级排布,层与层之间互相连接。在 MLP 中有三种类型的层,即:输入层(input layer)、隐藏层(hidden layer)和输出层(output layer)。输入层接收输入模式而输出层可以包含一个分类列表或那些输入模式可以映射的输出信号。隐藏层调整那些输入的权重,直到将神经网络的误差降至最小。对此的一个解释是,隐藏层提取输入数据中的显著特征,这些特征有关于输出的预测能力。
映射输入:输出
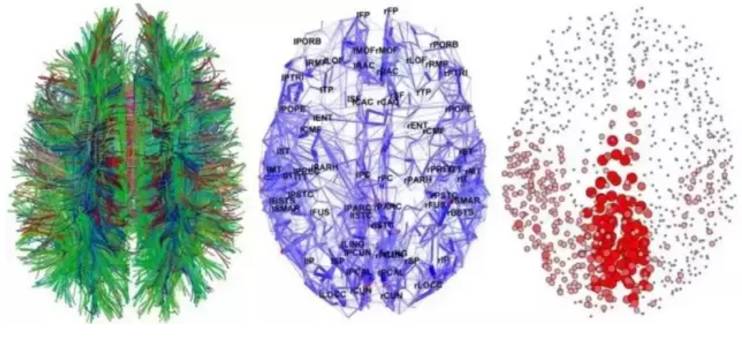
感知器接收输入向量,z=(z1,z2,…,zn)z=(z1,z2,…,zn),包含 n 个属性。该输入向量被称为输入模式(input pattern)。这些输入再通过属于感知器的权重向量 v=(v1,v2,…,vn) 进行加权。在多元线性回归的背景中,这些可被认为是回归系数或 β 系数。感知器的净输入信号通常是输入模式和其权重的总和产物。使用该总和产物得到净值(net)的神经元被称为求和单元(summation unit)。
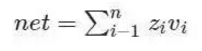
净输入信号减去偏差 θ 后被输入一些激活函数 f()。激活函数通常是单调递增函数,其值位于 (0,1) 或 (-1,1) 之间(本文后面将进一步对此进行讨论)。激活函数可以是线性的,也可以是非线性的。

下面是神经网络中一些常见的激活函数:

依次为:线性函数、阶跃函数、斜坡函数、S 型函数、双曲正切函数、高斯函数
最简单的神经网络只有一个映射输入到输出的神经元。对于给定模式 p,该网络的目标是相对一些给定的训练模式 tp 的一些一只的目标值来最小化输出信号 op 的误差。比如,如果该神经元应该映射 p 到 -1,但却将其映射到了 1,那么,根据距离的求和平方测定,神经元的误差为 4,即 (-1-1) 分层
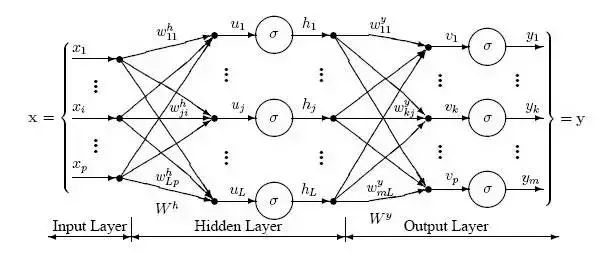
如上图所示,感知器被分层进行组织。感知器的第一层被称为输入层,它接收训练集 PT 中的模式 p. 最后一层映射到这些模型的预期输出。举一个输出的例子:模式可以是关于安全性的不同技术指标的数量列表,而潜在的输出则可能是 {买进、持有、卖出} 这样的分类。
隐藏层则将前一层的输出作为下一层的输入;而下一层的输出又会作为另一层的输入。所以,这些隐藏层到底在做什么?一个解释是,它们提取输入数据中的显著特征,这些特征可以预测输出。这个过程被称为特征提取(feature extraction),而且在某种程度上,其和主成分分析(PCA)等统计技术具有相似的功能。
深度神经网络具有大量隐藏层,有能力从数据中提取更加深层的特征。最近,深度神经网络在图像识别问题上取得了异常优异的表现。图像识别中的特征提取的图示如下:

除了过拟合(overfitting)的明显风险,我认为,用于交易的深度神经网络,在使用上所面临的一个问题是该神经网络的输入几乎总是经过了严重的预处理,这意味着实际可以提取的特征可能非常少,因为输入已经是某种程度的特征了。
学习规则
正如前面提到的那样,神经网络的目标是最小化一些错误度量(measure of error) ε. 最常见的错误度量是误差平方和(Sum squared error (SSE));尽管在金融市场的应用中,这种度量对异常值很敏感,而且可能没有跟踪误差(tracking error)那样合适。
误差平方和:
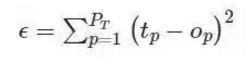
鉴于该网络的目标是最小化 ε,我们可以使用一种优化算法调整该神经网络中的权重。神经网络最常见的学习算法是梯度下降算法,尽管也可能使用其它算法和潜在更好的优化算法。梯度下降算法的工作方式是,计算相对于神经网络中每一层的权重的误差偏导数,然后在与梯度相反的方向上移动(因为我们想最小化神经网络的误差)。通过最小化误差,我们可以最大化神经网络在样本中的表现。
数学表示神经网络(v)中的权重更新规则由下式给出:
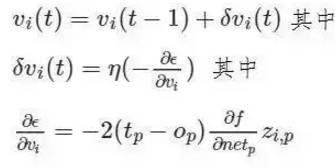
其中 η 是指学习率,控制着神经网络收敛的快慢程度。f 相对于模式 p 的净输入信号的偏导数的计算是所有非连续激活函数所面临的问题,这不值一提;这也是可能使用可选优化算法的一个原因。学习率的选择对神经网络的表现有很大的影响。较小值的 η 可能导致非常慢的收敛,而较高值的 η 则可能导致训练中的大量偏差。
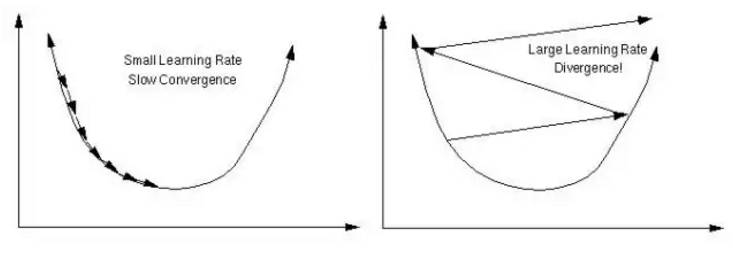
小学习率慢收敛,大学习率发散
总结
不管我遇见过的一些统计学家相信什么,神经网络不只是「懒人分析师的弱形式的统计学」(之前确实有人跟我这么说,而且这还挺有趣);神经网络代表了一种可追溯到几百年前的可靠统计方法的抽象。对于神经网络背后的统计学,我推荐阅读超棒的这一章(http://page.mi.fu-berlin.de/rojas/neural/chapter/K9.pdf)。话虽如此,但我同意,一些从业者喜欢将神经网络看作是「黑箱」,这样就可以在没有花时间了解问题的本质和神经网络是否是合适的选择的前提下,将神经网络应用于任何问题。在交易使用神经网络就是其中一例;市场是动态变化的,但是,随着时间的过去,神经网络假设输入模式的分布仍然保持静止。在《All Models are Wrong, 7 Sources of Model Risk》中可看到更详细的讨论。
3.神经网络流行许多不同的架构
到目前为止,我们已经讨论了最简单的神经网络结构,也就是多层感知器(multi-layer perception)。还有很多不同的神经网络结构(太多了,以至于难以在此提及),而且,任何神经网络的性能,是其结构和权重的一个函数。如今在机器学习领域中取得的许多进步,并非源自重新思考感知器和优化算法工作原理,而是创造性地思考如何融合这些组分。在下面,我会讨论一些非常有趣且富创造性的神经网络结构,递归神经网络(RNN)--一些或所有的连接倒流,意味着反馈环路存在于网络中。人们相信,这些网络能够在时间序列数据上表现得更好。照此说来,在金融市场的语境中,他们可能会特别相关。更多信息,请参见这篇很棒的文章《The unreasonable performance of recurrent [deep] neural networks.》
这张图表展示了三个流行的递归神经网络结构,即 Elman 神经网络,Jordan 神经网络与 Hopfield 单层神经网络。
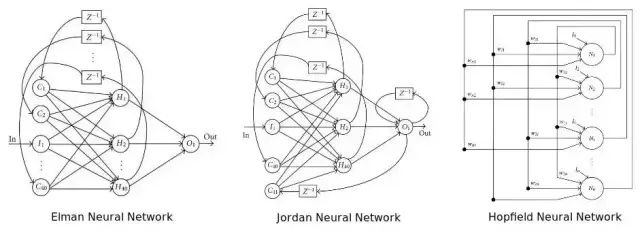
一个更新近、有趣的递归神经网络结构是神经图灵机器(Neural Turing Machine),结合了存储器与一个递归神经网络。事实已经证明,这些神经网络是图灵完全(Turing complete)的,并能够学习分类算法和其他计算任务。
Boltzmann 神经网络--最早的全连接神经网络之一,也就是 Boltzmann 机。这些网络是第一批能够学习内部表征、解决非常难的组合数学问题的网络。对 Boltzmann 机的一个解释是这样的:Hopfield 递归神经网络的蒙特卡洛版。尽管如此,很难训练神经网络,但是,受到约束时,会比传统神经网络更有效。给 Boltzmann 机施加限制,最流行的做法就是不准许隐藏神经元之间建立直接联系。这一特殊结构被称为受限 Boltzmann 机(Restricted Boltzmann Machine),被用于深度受限 Boltzmann 机(Deep Botlzmann Machines)。
![]()
图表展示了不同的波兹曼机(带有不同节点连接),如何能显著影响神经网络结果
深度神经网络--有着多层隐藏层的神经网络。近些年,深度神经网络已经成为最流行的网络,因为在图像和声音识别方面,它们取得了前所未有的成功。深度神经网络架构数量正在迅速增长,一些最受欢迎的架构包括深度信任网络(Deep Belief Networks),卷积神经网络,深度受限波兹曼机,栈化自动编码器,等等。深度神经网络最大问题之一,尤其是不稳定的金融市场环境下,是过度拟合。
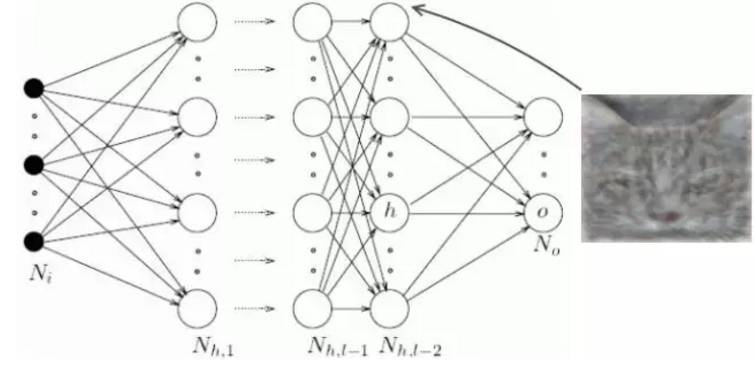
多个隐藏层组成的深度神经网络
自适应神经网络(Adaptive Neural Networks)--能够在学习中同时自适应、并优化自身结构的神经网络。实现这一点,要么是靠发展结构(添加更多隐藏层)或压缩结构(修剪不必要的隐藏层)。我相信,自适应神经网络是最适合金融市场的网络,因为市场具有动态性。之所以这么说,是因为神经网络所读取的特征可能会随着时间和市场的变化而有所加强或减弱。这意味着,过去收效很好的架构也需要修改,才能在今天达到最好的效果。
两个不同类型的自适应神经网络结构。左图是级联神经网络(cascade neural network),右图是自组织映射。
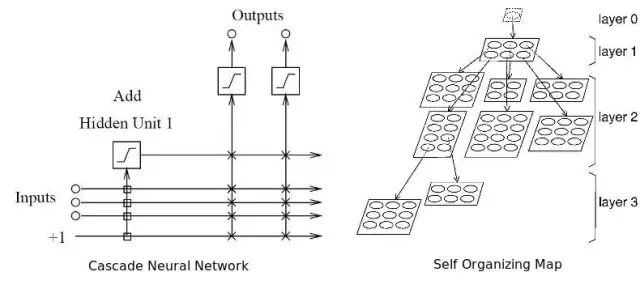
径向基函数网络(Radial basis networks)--尽管从感知与连接上来说并不是一个不同类型的结构,径向基函数网络利用径向基函数作为它们激活功能,这些是真实的重要功能,其输出从一个特定的角度来看取决于距离。最常用的径向基函数是高斯分布。由于径向基函数可以采用更加复杂的形式,他们最初用于执行函数插值。因此径向基函数神经网络可以有一个更高的信息能力。径向基函数还用于支持向量机(Support Vector Machine)的内核。
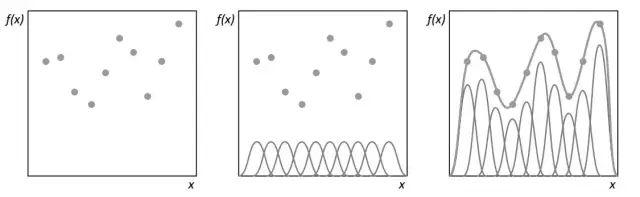
利用径向基函数,如何实现曲线拟合
总之,有数百个神经网络结构,而且一个神经网络性能可以会显著优于另一个。有兴趣使用神经网络进行量化分析的人,可能要测试多个神经网络结构,并结合它们的输出一起考虑,要从总体上最大化他们的投资成绩。利用神经网络进行交易之前,我建议先阅读我写的《All Your Models are Wrong,7 Sources of Model Risk》,因为里面谈到的不少问题仍然有用。
4.规模很重要,但并不是越大越好
选择了一个架构后,你还要决定神经网络的规模大小。多少输入?应该使用多少隐藏神经元?又有多少要用的隐藏层(如果我们用的是深度神经网络的话)?多少输出神经元?这些问题之所以十分重要是因为如果神经网络太大(或太小),神经网络可能会出现过度拟合(或拟合不够),也就是说,网络无法顺利泛化样本。
该利用多少或哪些输入?
输入的数量取决于待决问题、可提供数据的数量和质量,或许还需要一些创造力。输入是一些简单的变量,我们相信,这些变量具有一些预测能力,可以根据被预测的因变量进行一些预测。如果不清楚某个问题的输入,你可以系统地决定哪个变量应该被包括在内,方法就是观察潜在自变量和因变量之间的相关性和互相关。这种方法在《What Drives Real GDP Growth?》中有详细介绍。
利用相关性去选择输入变量,存在两个问题。首先,如果你正在使用一个线性相关矩阵,你也许会不小心排除了有用的变量。第二,两个相对不相关变量,结合在一起,可能会产生一个强相关变量。如果孤立观察变量,你也许会错失这一良机。为了克服第二种问题,你应该利用主成分分析去获取有用的特征向量(变量的线性结合),并将它们作为输入。这里的问题是,特征向量也许不能很好地泛化,而且它们还假设输入模式分布是固定的。
选择变量过程中会遇到的另一个问题,就是多重共线性。多重共线性是指,正被输入到模型中的独立变量中,有两个或更多的独立变量是高度相关的。在回归模型的语境下,这种情况可能会引发回归系数根据模型或数据的细微改变而不规律地变化。鉴于神经网络和回归模型是相似的,我怀疑神经网络也会存在这个问题。
最后,但并非不重要的是,当选择变量是基于省略变量的偏见时,或许会引发统计学上的偏见。当创建一个模型,这个模型遗漏了一个或者更加重要的原因变量时,省略变量偏见会出现。
当模型通过过度或低估某个其他变量影响的方式,不正确地补偿漏掉的变量时,也会制造偏见。比如,权重会变得过大,或SSE(误差平方和)会过大。
我该使用多少隐藏神经元?
隐藏单元的最佳数目,是个细节问题。这也就是说,作为一条经验法则,隐藏层越多,过度拟合风险越大。当神经网络并没有学习数据的重要统计特征,而是「记忆」模式与他们可能收集到的任何噪音,过度拟合就会发生。在样本中,这个结果不错,但是,离开样本,这个结果没有说服力。如何避免过度拟合?在产业领域,有两种流行的方法:早期停止(early stopping)和规则化(regularization),而我个人最喜欢的方法--全程检索。
早期停止,包括将训练组分为主要训练组和一个验证组。然后,不是以固定的迭代量来训练神经网络,而是训练网络,直到它在验证组上的表现成绩开始恶化。本质上,这能防止神经网络使用所有可以接触到的参数,并限制它简单记忆每一个所见模式的能力。这幅图显示了两个潜在的停止点(a 和 b)。

图片展示了神经网络在a到b进行阻止后的效果与过度拟合
规范化是指,神经网络利用复杂结构时,对其进行惩罚。可以根据神经网络权重大小来衡量这一方法的复杂性。可以这样实现规范化,添加一个条件(term),求平方误差目标函数,这个函数取决于权重大小。这相当于添加一个先验(prior),让神经网络相信它正在逼近的函数是平滑的。