背景介绍
接下来我们将用几篇文章介绍生存分析的内容,生存分析的应用非常广泛,可以用在很多不同的领域,分析不同实验条件下,研究对象“生存时间”的分布情况,从而了解实验条件对生存时间的影响。这里的“生存时间”不是专指人或动物的生命延续时间,而是泛指某个事件发生前的延续等待时间。例如:一个工人从下岗后到实现再就业的时间;一台汽车从开始使用到发生第一次故障的时间;一个病人从确诊患病到死亡的时间等。之所以用“生存”分析这个名称,是因为这种分析技术常用于描述病人在接受某种治疗后,他们存活时间的分布情况。
几个概念
生存分析的目的就是研究在不同因素下,生存时间的分布情况。要了解整个分析过程,首先需要了解几个专有名词的定义,这样才能保证分析数据的准确性。
事件及事件发生
事件是指研究者所关心的事件发生了,事件发生的时间点,也就是生存时间的记录终点。在生存分析中,定义清楚事件是非常重要的,直接关系到数据的记录是否准确。例如,在医学病症研究中,事件可以指病人死亡或疾病复发;在工业制造业中,事件可以指机器发生故障或发生产品质量事故;在社会管理中,事件可以是一个人失业后的再就业。需要注意,事件的定义一定要在数据收集之前完成,而不是没有定义清楚事件就开始收集数据,否则很可能做的是无用功。
生存时间
生存时间是指从某一起点开始到所关心事件发生的时间。因为生存时间是生存分析的分析对象,所以对生存时间的长度确定至关重要。
事件发生的时间点(计时终点)一般是明确的,例如患者死亡,机器故障,失业青年找到工作,而计时的起点有时却令人头疼,例如计算某些疾病的生存时间,那么计时的起点是疾病发生的时间点,但是某些慢性疾病(糖尿病等)的发病时间往往无法准确确定,其生存时间的起点也就无法准确确定。
生存时间的“时间”不一定是年月日时分秒等单位,例如,机器设备的生存时间,有时候以使用时间作为生存时间是不妥当的。比如计算汽车的生存时间,如果将汽车买来后到发生故障的使用时间作为生存时间,而在这段时间内,汽车很可能是长期闲置的,所以此时应该将汽车的行驶里程作为生存时间。
删失/失访
删失是指事件发生未被观测到或无法被观测到以至于生存时间无法被准确记录下来的情况。删失分为右删失、左删失和期间删失三种。只知道生存时间大于某一时间点,这种删失称为右删失;只知道生存时间小于某一时点的删失称为左删失;只知道生存时间在某一段时间之内的删失称为区间删失,右删失的情况最为常见。虽然删失使得生存时间无法准确计算,但在生存分析时还是应该将其考虑在内,因为删失数据会影响到最终的生存率结果。
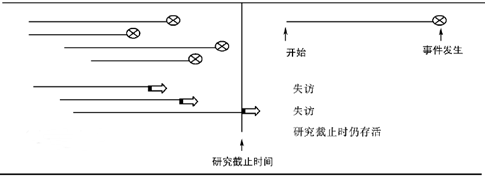
生存分析原理
生存分析刻画的是生存时间的分布情况,这里的分布指的是概率分布,如何形象刻画生存时间的分布情况呢?可以用一个二维坐标图来描述,横轴是时间长度,纵轴是事件发生概率,这就能很清楚的知道生存时间的概率分布情况了。
因为涉及到概率,那么自然要用概率函数来表示。根据计算概率的不同,生存分析的概率函数有两种:风险函数和生存函数。生存函数和风险函数是用来描述生存时间的分布的两个主要工具。
用一个非负随机变量T来表示生存时间,生存函数定义为随机变量T越过某个时点t时,所有考察对象中,没有发生事情的概率,也就是生存下来的概率。当t=0时,生存函数的取值为1,随着时间的推移(t值增大),生存函数的取值逐渐变小,生存函数是时间t的单调递减函数。可以用下面的式子表示生存函数:

根据生存函数,又可以提出累积风险函数,它的公式为:
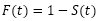
表示生存时间T为超过时间点t时,研究对象中,已经发生事件的概率。此外还有一个风险概率密度函数,它是累积风险函数的导数,公式如下:
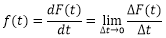
风险概率密度函数表示某个时间点t上,事件发生的概率。
通过以上公式,最终我们可以得到风险函数,计算公式为:
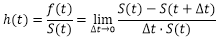
表示生存时间T达到时间点t时,在接下来一瞬间,事件发生的概率。
从上面的结果可知,风险函数和生存函数是可以互相推导的,因此在生存分析中,既可以生存函数,也可以用风险函数,一般生存函数的运用更多。这就好像测量汽车速度,可以测量瞬间速度,也可以通过测量距离和行驶时间计算平均速度,瞬时速度的测量通常是比较困难的,而且容易受到随机误差影响。
SPSS的生存分析
从下图可知,SPSS提供的生存分析包括四个子菜单:寿命表、Kaplan-Meier、Cox回归和考虑具有时间依存性协变量的Cox回归。
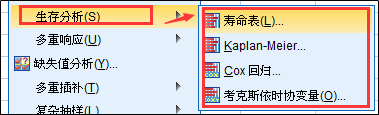
不考虑其它实验外因素(混杂因素),只考虑某个分类变量组间的生存时间分布情况,可以使用Kaplan-Meier法和寿命表法。这两种方法之间的区别在于生存时间的记录方式不同,Kaplan-Meier法的生存时间是通过记录事件发生准确时间点得到的,而寿命表法则适用于事件发生的时间点无法准确记录,只能确定事件发生在某段时间内,例如,癌症复发事件,复发的时间往往无法准确记录,只能通过定期复查来追踪。
Cox回归又称为比例风险模型,Cox回归比寿命表法和Kaplan-Meier法的应用范围更广,它能够同时考虑多个自变量对生存时间分布的影响。
具有时间依存性协变量的Cox回归,这种分析是建立在Cox回归模型基础之上的,某些情况下,有些协变量对生存时间分布的影响是随时间变化而变化的,此时原来的Cox回归模型的拟合结果不够准确,需要进行时间校正,这就是时间依存协变量Cox回归模型能够解决的问题。
总结一下
本篇文章对生存分析的分析原理进行了概括介绍。从原理出发,我们就能很好理解生存分析能够应用于很多不同的领域,包括医学、社会学和工业制造等等。接下来,我们将会按照SPSS的生存分析子菜单分别介绍Kaplan-Meier法、寿命表法、Cox回归和考虑时间依存协变量Cox回归的应用方法和案例分析。
温馨提示:








