kalman滤波是状态估计中的重要方法,在多传感器融合等应用领域也有广泛的应用。泡泡机器人公众号将用五次课程来详细介绍kalman的原理,课程中通过多个仿真实验以及案例的讲解让你深入了解kalman滤波算法。
本文著作权归作者范泽轩所有。本文获得作者授权在泡泡机器人公众号进行首发。
从今天开始我们就正式进入本系列课程的第一课啦,固定值的递推估计,首先跟我一起进入一个故事。
好吧,从现在开始你叫
falcao
(其实这是我的英文名字),你是一个大学生,你最大的爱好就是在你家的仓库里搞发明创造。现在寒假来了,你翻出了高中时候制作的一套钢铁侠盔甲,这套盔甲是你高中时期发明创造的得意之作,通过这套盔甲的制作,你熟悉了电子电路的基本制作,继电器控制电路、三极管控制电路、功放电路、一些门电路等基本电路的制作方法。这套盔甲在腿部有一套特殊装置,在按动开关时,会触发反作用力喷射系统喷射火焰。
马上就要到春节啦,你想送自己一套礼物,把你的钢铁侠盔甲升级一下,把它变成自动控制系统,你想在新年钟声敲响的时刻,穿着这套盔甲从你家的屋顶纵身一跃,在马上触地时,腿部的反作用力系统会自动触发,保证你安全的落地,通过实验测量,你觉得在离地面
0.3m
时,火焰喷射系统自动触发会保证你安全落地(我编的,不要信,哈哈)。
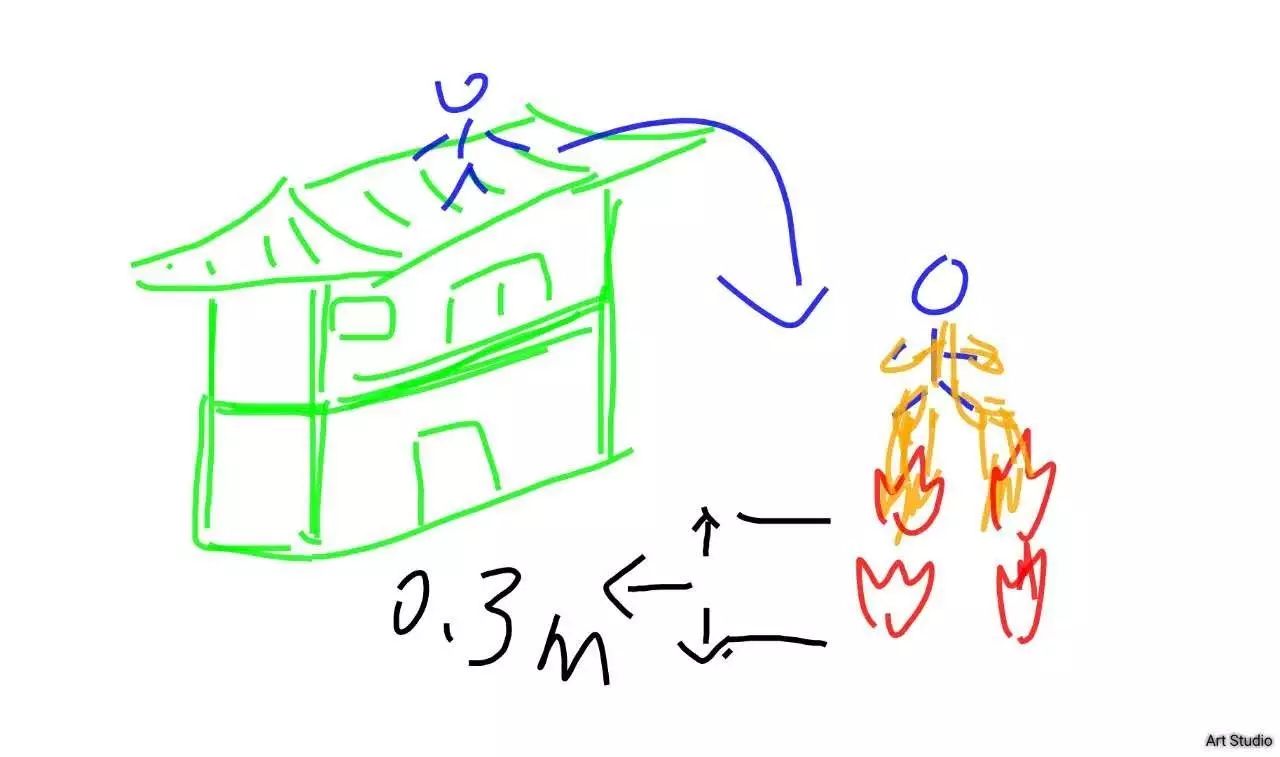
有了想法你开始着手制作单片机控制系统(类似于电脑的小型控制系统,可以编写
C
语言程序,控制外部连接的传感器),并选用超声波传感器来做外部测量传感器,用来测量你从屋顶跳下后距离地面的距离。
那么问题来了,你的超声波传感器经常波动,并传回一些错误的值,无论你如何更正硬件的滤波电路,超声波都会返回一些干扰,这样导致有的时候,你还没有离地面
0.3m
或超过
0.3m
时才触发喷射系统,太不稳定也太不精确了,你不想只停留在这样的初级电子制作水平,你开始思考,火箭在高速运动的情况下都可以精确的得出自己的方位信息,难道它使用的传感器就不会出现信号干扰和误差吗。

通过查阅各类书籍,你才明白从传感器返回的值不可能是实时的真实值,为了得到当前时刻最接近于真实值的反馈,我们要对传感器进行最优估计,而最经典且应用最广泛的最优估计方法就是应用
kamlan
滤波的线性系统估计,尤其是与运动控制系统相结合的估计中,
kamlan
方法的地位在最优估计领域不可替代。
2.1 应用实例
你开始按照
kalman
的方法一步一步的解决你传感器的干扰问题,首先你做了一个非常简单的近似,把每次测量的当前高度视为前一次测量的高度的一小部分。例如,如果每次测量得到你穿着盔甲下落时损失
2%
的高度,那么它在当前时间的高度是上一次的高度的
98%
。
高度
当前
= 0.98 *
高度
上一次
(
1.1
)
为了和各种书籍接轨,我们改用字母公式表述
1.1
。
altitude
current_time
= 0.98*altitude
previous_time
(
1.1
)
此时,你假设你的测量系统模型如下:
observed_altitude
current_time
= altitude
current_time
+ noise
current_time
(
1.2
)
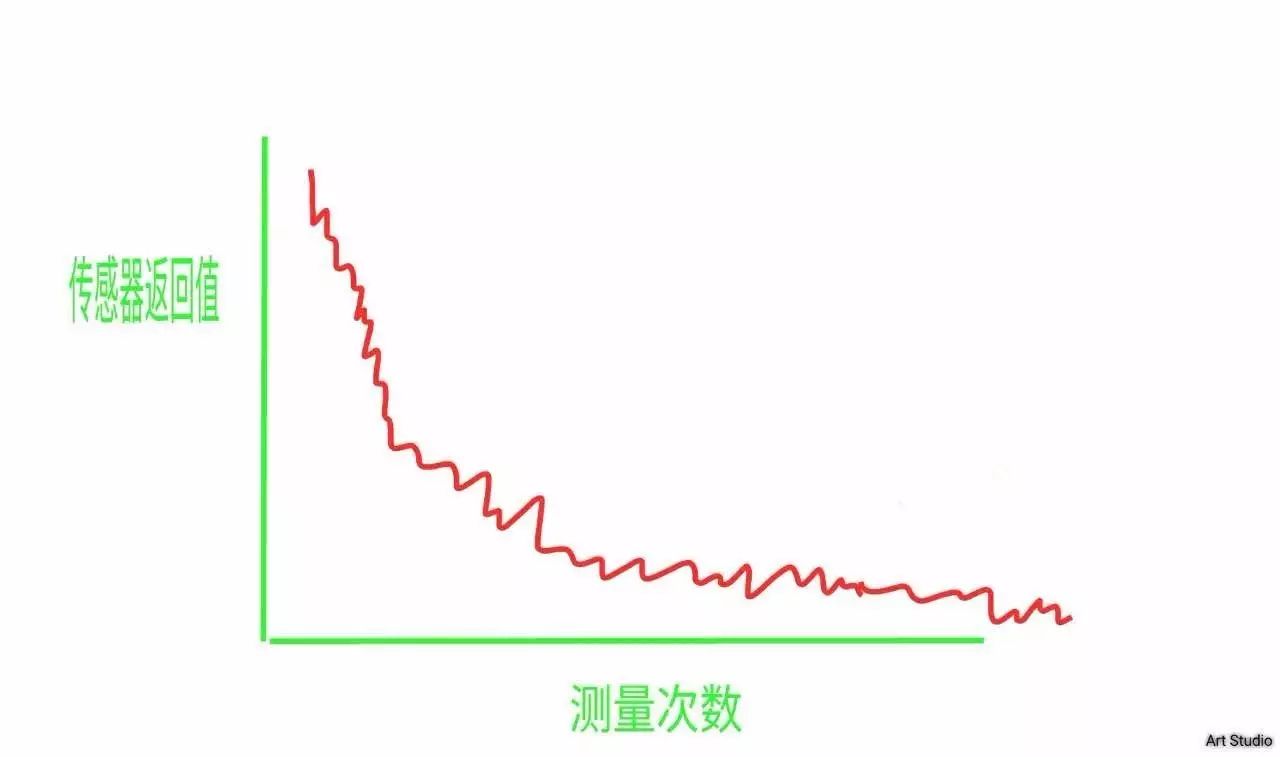
你发现这个测量系统和你的真实系统近似,超声波传感器就是返回这样波动的数值。
2.2 状态空间模型
此时,你有了两个模型
1.1
和
1.2
来描述系统,然而一般的工程师会使用
x,y
这样的变量符号来描述数学模型。所以
1.1
和
1.2
可以改写成:
X
k
= aX
k-1
(
1.1
)
Z
k
= X
k
+ V
k
(
1.2
)
V
k
就是噪声(干扰),此刻你为了模型更加精确,更加符合实际系统,你改进了
1.1
,加入了系统模型噪声
W
k
。系统模型变为:
X
k
= aX
k-1
+
W
k
(
1.1
)
W
k
为系统噪声,实际中也是如此,运动学模型都是理想的,不可能完全符合实际模型,加入
W
k
可以增加模型准确性。
此刻你觉得自己好高大上,可以用数学方法表述自己要完成的运动过程了,虽然有些简陋。你继续查阅
kalman
的相关知识。你的目标很明确就是要从超声波传感器的观测值中得出最接近于实际的测量估计值,很快你发现了一个很多相关书籍中都有描述的公式:

你迫不及待的要继续下去,没有功夫关心它是怎么来的,你只知道
g
k
被称作卡尔曼增益。善于观察的你注意到了两个特殊情况(
g
k
=1
或
g
k
=0
时),并尝试进行理解。
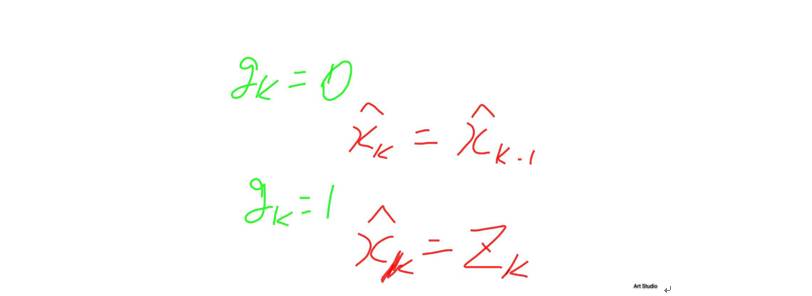
你忽然豁然开朗,
g
k
就是一个权重,控制你的最优估计更多的相信运动学模型的估计值或是更多的相信测量系统的返回值。
那么,我们如何计算的增益?答案是:间接地,从噪声。回想一下,每个观察都有一个特定的噪声值:
Z
k
= X
k
+ V
k
(
1.2
)
我们不知道每一个观测的噪声值可能是多少,但我们通常知道平均噪声:例如,我们大量实验得出超声波传感器的平均误差为
R
;没有下标因为它不取决于时间,而是一个传感器的性能。然后就可以根据
R
来计算
g
k
了。
你了解到关于
g
k
,
kalman
给出了相关的公式如下:
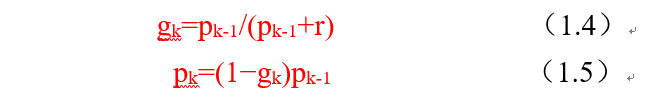 pk
是预测偏差,从两个公式可以看出它只是一个递归循环的变量,所以它的初始值也许并不重要。
pk
是预测偏差,从两个公式可以看出它只是一个递归循环的变量,所以它的初始值也许并不重要。
你同样不想管它是怎么得到的,但是善于观察的你再次发现:
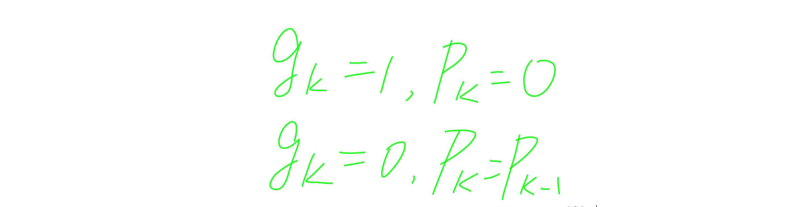
也就是说
g
k
= 1
时,系统的预测偏差为
0
,而
g
k
=0
时,系统的预测偏差并没有更新。
而进一步从运动系统中预测偏差,
kalman
给出了如下公式:
P
k
= a*P
k
*a (1.6)
2.3 卡尔曼滤波标准公式
了解到以上的一些基本公式后,你从
kalman
的论文中得到了整个应用
kalman
方法的步骤需要如下
5
个公式:
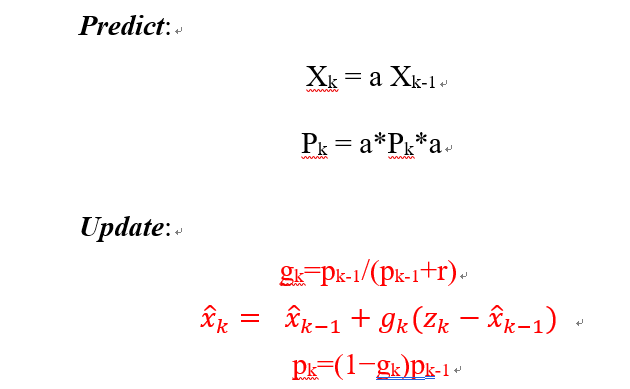
于是你开始按照公式编写
C
语言程序,烧写进入单片机去处理你的超声波传感器的返回值。
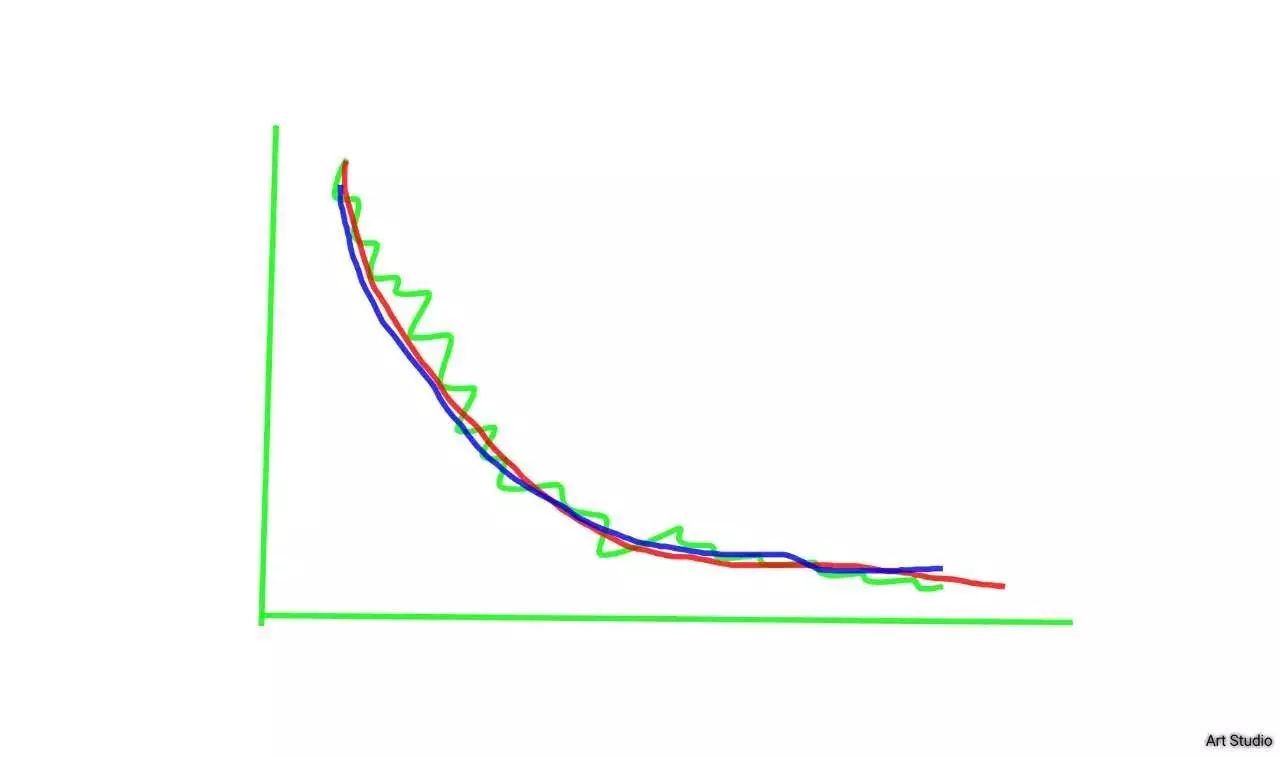
你发现红色的
kalman
滤波值,不仅连续稳定,也很接近绿色的真实值。你喜出望外,不过你开始考虑,我不能只会简单的使用啊,好歹我也是大学生,我要从理论上深入理解,你决心开始关心卡尔曼滤波背后的数学推导了。
2.4 数学推导
那么,一个很久很久以前的传说就浮出了水面,卡尔曼滤波器的起源,一个著名的估计问题,即利用批处理方法估计一个固定量。
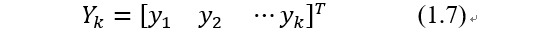
且
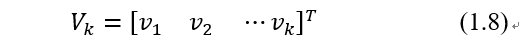
量测方程定义了误差
V
k
、待估计量
X
和量测
Y
k
的关系为:
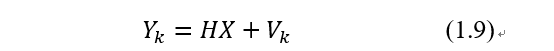
假定误差为零均值,协方差为:
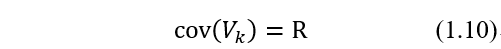
利用协方差的逆矩阵作为加权阵构造最小化函数:
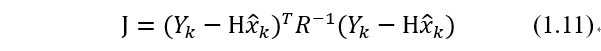
试图找到满足上式最小的
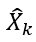 。采用协方差阵的逆矩阵作为加权阵,可以增加小量测误差的影响。该问题的最小二乘解是:
。采用协方差阵的逆矩阵作为加权阵,可以增加小量测误差的影响。该问题的最小二乘解是:
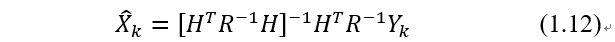
为了得到估计误差的协方差,首先将式(
1.9
)的
Y
k
代入上式可得:
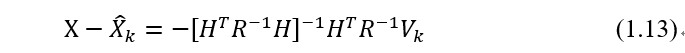
注意到误差的期望为
0
,对上式的外积求期望得到协方差:
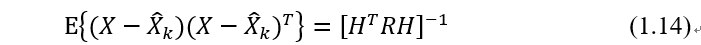
用
P
k
表示可得:
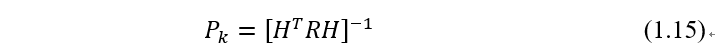
看到以上内容你开始心潮澎湃,以前的漫无目的变成了现在的有理有据,聪明的你发现这样分析问题比以前单一的改变调试参数,使用一些均值滤波、连续滤波简单的滤波方法来比更加具有理论依据,也更加具有科学意义。
这种批处理方法估计固定值,非常适用于你的钢铁侠减速系统,可你又开始担心你的单片机的处理能力,因为通过以上方法,每一次超声波测量的数据你都必须要存储起来,这样你才能通过更新
Y
k
和
R
来更新估计
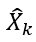 和
和
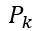 ,并再循环更新
R
和
,并再循环更新
R
和
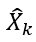 。你开始寻找一种可以不去每次都重新处理旧的量测的方法,显而易见,通过一种递归的方法引入数据来修正过去的估计值是最佳的途径。
。你开始寻找一种可以不去每次都重新处理旧的量测的方法,显而易见,通过一种递归的方法引入数据来修正过去的估计值是最佳的途径。
从此刻,你便机缘巧合的进入了本节课的重点内容,也即将进入
kalman
的
5
个公式的全面推导,固定量的递推估计方法。
长按下图,识别图中二维码,关注“泡泡机器人SLAM”(ID:paopaorobot_slam)公众号。
系列全文PDF下载链接在【泡泡机器人原创专栏】第 5 课 UKF 与粒子滤波实现中给出
,敬请关注。

【版权声明】
泡泡机器人SLAM的所有文章全部由泡泡机器人的成员花费大量心血制作而成的原创内容,希望大家珍惜我们的劳动成果,转载请务必注明出自【泡泡机器人SLAM】微信公众号,否则侵权必究!同时,我们也欢迎各位转载到自己的朋友圈,让更多的人能进入到SLAM这个领域中,让我们共同为推进中国的SLAM事业而努力!
【注】
商业转载请联系刘富强([email protected])进行授权。普通个人转载,请保留版权声明,并且在文章下方放上“泡泡机器人SLAM”微信公众账号的二维码即可。
【编辑】
徐武民




