【学习】稀疏学习综述

       稀疏学习是近年来机器学习和模式识别领域的一个研究热点，在本文中，我们给出了稀疏学习综述。稀疏学习已经应用到机器学习和模式识别的很多子领域，包括分类、聚类和子空间学习等，本文侧重在结构化稀疏学习在特征选择方法中的应用。

       特征选择，是许多模式识别任务中一个重要的成分。在这些任务中，人经常面临高维数据。特征选择算法是用来从原始的特征子集中选择相关的特征子集，这样有利随后的分析比如分类和聚类。在最近一些年来，基于结构化稀疏的特征选择算法被广泛地研究，已经有大量算法被提出。然而，关于这些结构化稀疏的特征选择算法之间的联系以及他们是如何演化的，没有得到系统的研究。我们系统总结了基于结构化稀疏的特征选择方法，包括它们的研究动机和数学表达。我们探究了不同方法之间的关系，提出一个分类方法来阐明它们的演变。我们将已有的结构化稀疏的特征选择方法分成两类：基于向量的特征选择(基于lasso的特征选择)和基于矩阵的特征选择(基于矩阵的r,p范数的特征选择)。而且，为了特定的应用，特征选择已经和其他机器学习方法融合在一起，比如多任务学习、多标记学习、多视图学习、分类和聚类等。我们不仅基于回归和正则化策略比较了这些方法的区别和联系，而且对工作在相关领域的从业者提供了有用的指导，指导他们如何来做特征选择。所有的方法都总结在以下的图中。

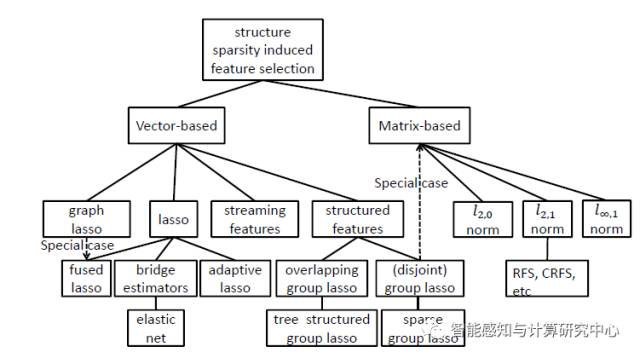
图1. 基于结构化稀疏的特征选择的分类

原文链接：

https://mp.weixin.qq.com/s/RjTQe430YZp_WEZgZzE-vQ