(点击
上方公众号
,可快速关注)
转自:刘毅
https://61mon.com/index.php/archives/193/
好文投稿, 请点击 → 这里了解详情
直接插入排序
直接插入排序(Insertion Sort)可以说是排序里最简单的了。为简化问题,我们下面只讨论升序排序。
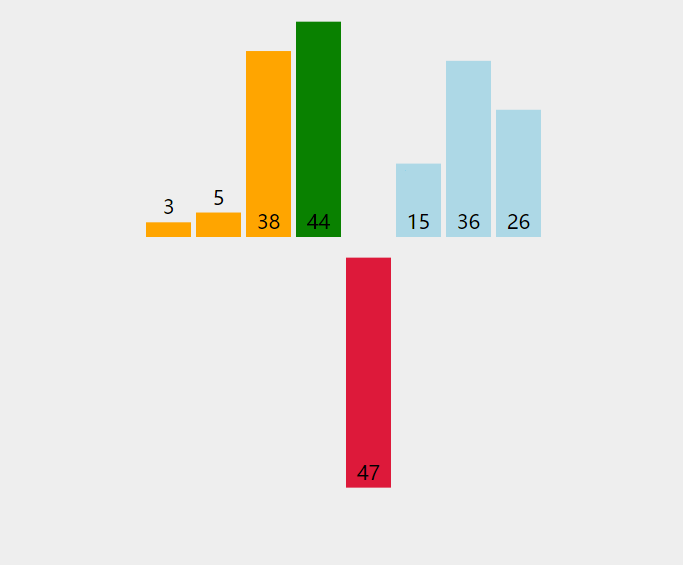
代码如下:
void
InsertSort
(
int
array
[],
int
left
,
int
right
)
{
int
temp
;
int
j
;
for
(
int
i
=
left
+
1
;
i
<=
right
;
i
++
)
{
temp
=
array
[
i
];
j
=
i
-
1
;
while
(
j
>=
left
&&
array
[
j
]
>
temp
)
array
[
j
+
1
]
=
array
[
j
--
];
array
[
j
+
1
]
=
temp
;
}
}
那么它的算法复杂度如下:
时间复杂度
1、最好情况,序列是升序排列,在这种情况下,只需进行 n-1 比较,即 Tbest(n)=O(n);
2、最坏情况,序列是降序排列,那么此时需要进行的比较共有 12n(n−1) 次,即 Tworse(n)=O(n2);
3、平均情况,为 Tavg(n)=O(n2)。
空间复杂度
由程序很容易得 S(n)=O(1)。
直接插入排序不适合对于数据量比较大的排序应用。但是,如果需要排序的数据量很小,例如量级小于千,那么直接插入排序还是一个不错的选择,因此在 STL 的 sort 算法和 stdlib 的 qsort 算法中,都将直接插入排序作为快速排序的补充,用于少量元素的排序(通常为 8 个或以下)。
此外直接插入排序有两个常用的优化:二分查找插入排序,希尔排序。下面分别介绍。
二分查找插入排序
因为在一个有序序列中查找一个插入位置,所以可使用二分查找,减少元素比较次数提高效率。
/* 给定一个有序的数组,查找第一个大于等于 value 的下标,不存在返回 -1 */
int
BinarySearch
(
int
array
[],
int
n
,
int
value
)
{
int
left
=
0
;
int
right
=
n
-
1
;
while
(
left
<=
right
)
{
int
middle
=
left
+
((
right
-
left
)
>>
1
);
if
(
array
[
middle
]
>=
value
)
right
=
middle
-
1
;
else
left
=
middle
+
1
;
}
return
(
left
<
n
)
?
left
: -
1
;
}
void
BinaryInsertSort
(
int
array
[],
int
left
,
int
right
)
{
for
(
int
i
=
left
+
1
;
i
<=
right
;
i
++
)
{
int
insert_index
=
BinarySearch
(
array
,
i
,
array
[
i
]);
if
(
insert_index
!= -
1
)
// 如果可以插入到前面的有序序列中
{
int
temp
=
array
[
i
];
int
j
=
i
-
1
;
while
(
j
>=
insert_index
)
{
array
[
j
+
1
]
=
array
[
j
];
j
--
;
}
array
[
j
+
1
]
=
temp
;
}
}
}
最好情况下,即序列为升序时,时间复杂度为O(logn)。
其它情况下,除了找到插入点所需的操作数从 O(n) 降为 O(logn) 外,其它的操作并未减小,其时间复杂度依旧是 O(n2)。
希尔排序
希尔排序,也称递减增量排序算法,以其设计者希尔(Donald Shell)的名字命名,该算法由 1959 年公布。
我们举个例子来描述算法流程(以下摘自维基百科):
假设有这样一组数 {13, 14, 94, 33, 82, 25, 59, 94, 65, 23, 45, 27, 73, 25, 39, 10},如果我们以步长为 5 开始进行排序:

然后我们对每列进行排序:

将上述四行数字,依序接在一起时我们得到:{10, 14, 73, 25, 23, 13, 27, 94, 33, 39, 25, 59, 94, 65, 82, 45},然后再以 3 为步长:
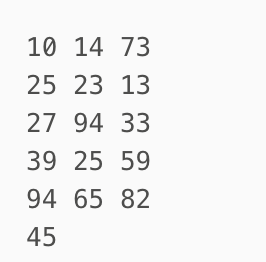
排序之后变为:
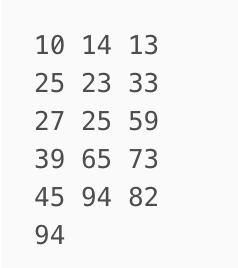
最后以 1 为步长进行排序(此时就是简单的插入排序了)。
可想而知,步长的选择是希尔排序的重要部分。
算法最开始以一定的步长进行排序,然后会继续以更小的步长进行排序,最终算法以步长为 1 进行排序。当步长为 1 时,算法变为直接插入排序,这就保证了数据一定会被全部排序。
Donald Shell 最初建议步长选择为 n2,并且对步长取半直到步长达到 1。虽然这样取可以比 O(n2) 类的算法(直接插入排序)更好,但这样仍然有减少平均时间和最差时间的余地。
可能希尔排序最重要的地方在于当用较小步长排序后,以前用的较大步长仍然是有序的。比如,如果一个数列以步长 5 进行了排序然后再以步长 3 进行排序,那么该数列不仅是以步长 3 有序,而且是以步长 5 有序。
如果不是这样,那么算法在迭代过程中会打乱以前的顺序,那就不会以如此短的时间完成排序了。

已知的最好步长序列是由 Sedgewick 提出的 {1, 5, 19, 41, 109, ...},该序列的项来自 9⋅4i−9⋅2i+1 和 2i+2⋅(2i+2−3)+1 这两个算式。
这项研究也表明比较在希尔排序中是最主要的操作,而不是交换。
用这样步长序列的希尔排序比插入排序要快,甚至在小数组中比快速排序和堆排序还快,但是在涉及大量数据时希尔排序还是比快速排序慢。
另一个在大数组中表现优异的步长序列是:{1, 9, 34, 182, 836, 4025, 19001, 90358, 428481, 2034035, 9651787, 45806244, 217378076, 1031612713, …}(斐波那契数列除去 0 和 1,将剩余的数以黄金分区比的两倍的幂进行运算得到的数列)
void
ShellSort
(
int
array
[],
int
n
)
{















