主要观点总结
本文研究了混合膜谐振器(HMR)在声学硬边界条件(AHBC)下的超低频噪声吸收特性。通过腔体下表面具有三个开口的HMR作为声学软边界条件(ASBC)的新吸收机制,实现了在数十Hz至150Hz范围内的超低频噪声的宽带吸收。研究表明,能量耗散主要发生在开口区域。此外,研究还推导出具有理想AHBC和ASBC的吸收体的因果不等式,并实现了所提出吸收器的因果最优性。本研究为优良的超低频吸声器的设计提供了指导,有助于解决降噪问题。
关键观点总结
关键观点1: 混合膜谐振器(HMR)的超低频噪声吸收特性
HMR作为典型的AHBC超材料吸波体具有优异的噪声吸收能力,但面临实现超低频噪声宽带吸收的挑战。
关键观点2: 新的吸收机制
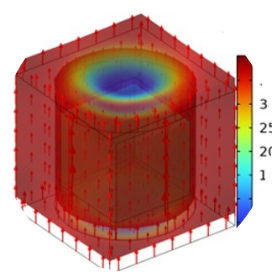
腔体下表面具有三个开口的HMR表现出一种新型吸收机制,其中能量耗散主要发生在开口区域而非膜中。
关键观点3: 因果不等式的推导
基于柯西积分和因果原理,研究推导出具有理想AHBC和ASBC的吸收体的因果不等式,并实现了吸收器的因果最优性。
关键观点4: 研究意义与影响
本研究为优良的超低频吸声器的设计提供了有价值的指导,有助于解决降噪的主要问题。同时,该研究成果为进一步优化和发展吸声器提供了理论支持。
正文


|
混合膜谐振器(HMR)作为一种典型的具有声学硬边界条件(AHBC)的超材料吸波体,表现出优异的噪声吸收能力,但挑战在于实现数十Hz至150Hz范围内超低频噪声的宽带吸收。在这项研究中,我们系统地研究了腔体下表面具有三个开口的 HMR 的吸收特性、吸收机制和偶然最优性,该 HMR 充当声学软边界条件 (ASBC)。与经过充分研究的 AHBC HMR 相比,首先发现了一种新的吸收机制,该机制表明大多数能量耗散发生在开口区域而不是膜中。因此,具有ASBC的HMR可以在非常小的厚度下表现出出色的超低频吸声性能,并且HMR的半峰全宽可以扩大7倍以上。此外,基于柯西积分和因果原理,推导出具有理想AHBC和ASBC的吸收体的因果不等式。还实现了所提出的吸收器的因果最优性。这项研究为优秀的超低频吸声器的设计提供了有价值的指导,有助于解决降噪的主要问题。
|









|
本文建立了一个在空腔下表面有三个开口的HMR,系统地研究了其吸收机理和随机最优性。研究表明,在空腔下表面有开口的HMR的开口区将引入一种新的吸收机制,其能量耗散主要发生在开口区,而不是发生在膜内。此外,ASBC的HMR在超低频的厚度下可以表现出优异的吸声性能,HMR的半最大值的全宽可以放大7倍以上。基于柯西积分和因果原理,导出了具有理想AHBC和ASBC的吸声器的因果不等式。在腔下表面有三个开口的HMR达到因果最优,即所考虑的HMR在指定的超低频带内具有最好的吸收性能。本研究为优良的超低频吸声器的设计提供了有价值的指导,有助于解决降噪的重要问题。
|
|
有关论文的更多信息请点击左下角
阅读原文
免责声明:本文中的部分资料来源于该期刊文章,转载目的在于传递信息及分享,并不意味赞同其观点或真实性,也不构成其他建议。本公众号仅提供交流平台,供广大读者学习,不为其版权负责。如涉及侵权、隐私等问题,请联系我们及时删除,同时也欢迎广大读者进行投稿交流。
投稿邮箱:
[email protected]
|