银行贷款的还款方式有等额本金法和等额本息法,它们各有什么利弊?哪一种还款方式利息多?每个月的还款额怎么计算?这篇文章通过数学计算告诉你!
经过多年的改革开放,人们的消费观念有了很大的变化。越来越多的人需要买房、买车,有的人还需要投资,钱不够怎么办?向银行贷款就成为很普遍的事情。
贷款就要还款,不但要还本金,还要付利息。
一般来讲,利息是按照利率来计算的,比如:向银行贷款30万元,也就是欠了银行30万元。如果月利为0.2%,每月就要付利息300000×0.2% =600(元)。
假定贷款30万元的期限是10年,一共是120个月。一种还款方式是
等额本金法
:将30万元的本金平均分到120个月去归还,每月归还300000÷120=2500(元)。
除了每月归还本金2500元,还需付利息。
第1月,由于还没开始归还本金,应当按照欠银行30万元来计算利息,应付利息600元。于是,第1月连本带利应当付给银行2500+600=3100(元)。
第2月,由于已经还了2500的本金,还欠银行本金300000-2500=297500(元),按此计算利息应为297500×0.2% =595(元)。
以后,每月归还本金2500元,欠银行本金每月减少2500元,应付利息每月减少2500×0.2% =5(元)。
第k月欠本金a
k
=300000-2500k(元),第k+1月应付利息为
a
k
×0.2%=(300000-2500k)×0.2%=600-5k (元),连本带利付2500+(600-5k)=
3100-5k
(元)。
等额本金还款法计算起来比较容易,但也有问题:由于所欠本金逐月减少,应付利息也逐月减少,每月连本带利付给银行的金额也逐月减少。每月还钱总额不相等,执行起来不够方便。更重要的是:开始还得多,后来就还得少。贷款者在一开始的还款压力相当大。更何况,贷款者之所以贷款,就是因为缺钱,而且往往在开始的时候更缺钱,这更加重了还款压力。因此就有另外一些还款方式。其中一种是
等额本息法
:每月付给银行的本金和利息的总额始终保持相等。
以下来计算每月连本带利应当付给银行多少钱,假定这个数额为c。我们来看c应当满足什么样的条件,根据条件列出方程,再解出c来。
由于应还本金的总数30万固定不变,关键是要算出每个月应付的利息。而每月应付的利息是前一个月末欠银行本金总额的0.2%。设第k月欠银行的本金额为a
k
,则a
0
就是还款之前欠款总数,应为a
0
=300000。第k+1月应付利息为0.002a
k
,归还的本金就是c-0.002a
k
,于是第k+1月欠款总额a
k+1
=a
k
-(c-0.002a
k
)=1.002a
k
-c。
以下根据数列a
k
满足的递推关系
a
k+1
=1.002a
k
-c
求出a
k
的通项公式,并选择适当的c满足条件a
120
=0。
如果c=0,则满足条件a
k+1
=1.002a
k
的数列{a
k
}是以1.002为公比的等比数列。现在的情况是c>0,我们将数列{a
k
}的各项同减去一个待定常数λ,使得数列{a
k
-λ}={a
0
-λ,a
1
-λ,a
2
-λ,……}成为等比数列,找出它的通项公式a
k
-λ=f(k),从而得到{a
k
}的通项公式a
k
=f(k)+
λ。
令b
k
=a
k
-λ,则a
k
=b
k
+λ,代入递推关系a
k+1
=1.002a
k
-c得到:b
k+1
+λ
=1.002(b
k
+λ
)-c,即b
k+1
=1.002b
k
+(0.002λ-c)。只要取 λ 使得0.002λ-c=0,则{b
k
}是等比数列。为此,只需λ=500c。
于是{b
k
}是以1.002为公比的等比数列,且b
0
=a
0
-λ=300000-500c,我们有:
b
k
=b
0
·1.002
k
=(300000-500c)·1.002
k
,
a
k
=(300000-500c)·1.002
k
+500c
=300000·1.002
k
-500c(1.002
k
-1),
由a
120
=0,可得
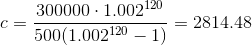
一般地,设向银行贷款总额为N,贷款时间为n个月,月利率为p,则可以同样的计算出等额本息每月应还款(包括本金与利息)金额为:
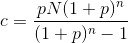
第k+1个月支付利息为d
k+1
=(pN-c)(1+p)
k
+c,归还本金为c-d
k+1
。
对于以上所举的具体数例N=300000元,n=120,p=0.002,按等额本息还款方案付给银行的总金额为2814.48×120=337737.60元,除去归还本金300000元,支付利息总额为37737.60元。而按等额本金还款方案,第k+1月支付利息为(600-5k)元,120个月支付的利息总额为:
600+595+…+5=36300(元)
两者相比较,等额本息还款方案支付的利息更高一些。这是什么道理呢?
在两种还款方式下,由于逐月归还本金,所欠银行本金逐月下除,因而支付的利息逐月下降。
按照等额本金还款方式,每月归还本金数额相等。
按照等额本息还款方式,由于每月还款总额不变,随着支付利息金额逐月下降,归还本金的数额逐月增加。
两种方案都在同样的时间120月内将本金还完,但是等额本金方式每月归还同样多的本金,而等额本息方式开始还得少,以后越还越多。这就意味着,等额本息方式归还本金总是比等额本金方式还得更慢,从第2个月开始一直到还款结束之前的任何一个月,按等额本息方式所欠银行的款都比等额本金的方式更多,因此每个月支付的利息更多。积累起来,当然等额本息方式支付的利息总额更多。
下表列出了每月初按两种还款方案已归还的本金总额。

由上表可以看出,等客本息方案第一归还本金2214.48元,比等额本金方式的2500元少。以后等额本息方案归还的本金虽然逐月增多,但每月已还本金的总额始终比等额本金方式少,一直到最后一个月(第120月末)赶上。这就意味着,在还款过程中的第一个月,等额本息方式的欠款都比等额本金方式欠得更多,应付的利息也更多。















