作者简介：王善平，1990 年华东师范大学数学系现代数学史方向硕士研究生毕业，师从张奠宙。现任华东师范大学学报编辑部编审，数学与人文丛书编委。已发表数学史、图书馆学、信息科学技术方面的论著30余篇/部。
（一）
德国物理学家伦琴（Wilhelm Conrad Röntgen）在1895年宣布发现了X射线，他因此获得1901年首届诺贝尔物理学奖。伦琴也许不曾想到，他的发现很快在医学诊断领域得到了广泛的应用。因为X射线具有强大的穿透能力，能够轻易地通过人体。这使得医生无需施用外科手术，就能窥探病人体内，从而做出准确诊断。
当X射线通过人体时，对于体内的不同组织，如肌肉、血管、骨骼、脏腑等，有不同的穿透率；体内病变的组织，如发炎或肿瘤，其X射线穿透率也与正常组织不同。所以如果让人体置于X射线源与感应胶片之间，就能在胶片上留下体内组织的X射线投影像，医生则可以根据影像来诊断病情。这就是传统的X射线成像仪的工作原理。
然而，由传统X射线成像仪所形成的人体内部纵向面的投影像，只包含了体内组织的二维结构信息，它无法提供体内横截面（断层）上组织的情况。所以，虽然它对于诊断骨折或肺部感染之类的病情有很大帮助，但对于诊断脑部疾病或内脏肿瘤之类的疑难杂症却无能为力。在很多诊疗场合，医生非常需要获得病人体内组织的断层结构信息。但只有切开身体，才能观察到体内断层，而这将不可避免地伤害病人，甚至危及生命。
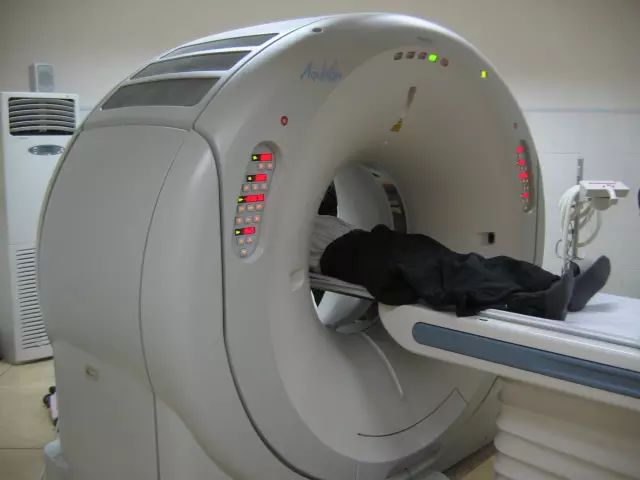
20世纪70年代中期，在英国出现了一种神奇装置，叫做“计算机辅助X射线断层成像仪”（Computer Assisted Tomography，简称CAT或CT）；它能够在不损伤病人的情况下，提供人体从头到脚各部位的断层X-射线图像。利用CT，医生可以轻而易举地观察到人体内部哪怕是微小的病变和病灶分布，能够及早采取正确的治疗措施，从而拯救了无数患者的生命。
1979年10月11日，诺贝尔的诞辰，位于瑞典首都斯德哥尔摩的卡罗琳医学院宣布，今年的诺贝尔医学奖授予美国人柯马克（Allan MacLeod Cormack，1924-1998）和英国人豪斯菲尔德（Sir Godfrey Newbold Hounsfield，1919-2004），以表彰他们“发明了计算机辅助X射线断层成像技术”。卡罗琳医院的葛雷茨（Torgny Greitz）教授在授奖发言中说[2]：“今年诺贝尔医学及生理奖的两位获奖者都不是医学专家，然而他们在医学领域掀起了一场革命…… 他们所发明的计算机辅助X射线成像技术，使医学如同进入了太空时代。”“没有什么医学成就能够像CT技术那样，立即被广泛接受并得到毫无保留的热烈欢迎。”“柯马克和豪斯菲尔德开创了医学诊断的新时代……（他们的工作）正符合诺贝尔在其遗嘱中有关‘为人类作出最有益贡献’的规定，没有几位诺贝尔医学生理奖的获得者能够达到像他们那样的符合程度。”
（二）
柯马克出生于南非的约翰内斯堡市，父亲是电信工程师，母亲是教师。父母亲都是第一次世界大战前不久，从苏格兰来到南非的移民。柯马克是家中三个孩子中最小的。这一家人总是随着父亲工作的变化而不停地搬迁；直到父亲于1936年去世，他们才在开普敦市安顿下来。柯马克的高中时代是在开普敦市的一所公立男子中学度过的，那时，他除了课余积极参加辩论赛、打网球以及偶尔出演话剧外，还对天文学产生了浓厚的兴趣。他如饥似渴地阅读了大量的天文学科普著作，从中学习到许多数学和物理学知识。
不过，在当时天文学并不是一个养家糊口的好职业，所以柯马克在考取开普敦大学以后，一开始还是追随父亲和哥哥的足迹，选择了电气工程专业；两年后又改学物理学专业。1944年获物理学学士学位，一年后获晶体学硕士学位。他在大学时代的课余爱好是登山和听音乐。
从开普敦大学毕业后，1947年，柯马克来到英国剑桥大学的卡文迪什实验室做研究生（Research Student）。在一次听著名物理学家狄拉克关于量子力学的讲座时，他邂逅美国姑娘巴巴拉·西维（Barbara Seavey），遂坠入爱河。一年半以后，两人准备结婚。于是，柯马克中断了在卡文迪什实验室的研究工作，带着未婚妻回到了南非开普敦大学物理系任讲师。
1956年，柯马克获得第一个学术休假年，他选择跟随妻子来到美国，在哈佛大学做回旋加速器实验。1957年秋，他接受了美国塔夫斯（Tuft）大学的邀请，任该校的物理系教授。他在这所大学一直干到1995年退休。其间，他于1966年加入美国籍，1968-1976年任物理系主任。在塔夫斯大学的数十年中，他的主要学术兴趣是原子核物理和粒子物理。而令他赢得诺贝尔奖的那些工作，只是他的业余爱好。
（三）
1955年，还是开普敦大学物理学讲师的柯马克接受到一项任务，要为南非一家医院的放射科监测肿瘤患者接受放射性同位素治疗的剂量。接受治疗的患者体内的同位素剂量及其分布应该受到严格的控制：如果同位素剂量太小，将达不到理想的疗效；剂量太大，则会危害患者的健康。同时，同位素的浓度应在肿瘤组织内较高，在健康组织内尽可能低。柯马克于是想，是否可以通过体外测量同位素发出的射线，来确定其在体内的浓度分布，以帮助医师确定最佳治疗方法？他很快发现这其实是一个数学问题，而且解决了这一问题可以有其他种种应用。他终于在1963年发表了题名为“函数的直线积分表示及其放射学应用”[4]的开创性论文。在该文的开头提到了所研究问题的解答有三个应用：（1）确定二维区域内X射线吸收率的变化；（2）确定物质中正电子湮灭的非均匀分布；以及（3）确定恒定成分物质中的密度变化。但只字未提到关于人体断层成像的应用——当时他根本没有想到。
柯马克的文章发表后，在好几年内无人理会。直到1970年代初期，由于计算机的迅速发展使得大规模数值运算成为可能；英国计算机工程师豪斯菲尔德制造出了CT第一台原型机，更多的学者开始研究CT的工作原理；这时人们才注意到，柯马克早在10年前就已经建立好了CT的完整理论。顺便提一下，后来与柯马克分享诺贝尔奖的豪斯菲尔德，是在二次大战中的军队里学习了电子技术。他甚至未曾获得过正规大学的毕业文凭。
（四）
CT是如何做到在不损伤病人的情况下获得病人体内横断层的图像的？如前所述，人体内部不同的组织具有不同的X射线吸收率（=1-穿透率）。所以，如果能够知道人体内X射线吸收率的分布，就可以重建体内组织的图像了。这正是CT所要做的。
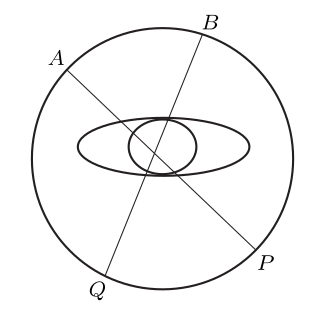
如图所示，一束X射线从一定点A穿过人体，到达P点。由于在途中经受不同物质的吸收，所以在P点接收到的X射线的强度较在A点出发时有了一定的衰减，其衰减程度与AP间物质的平均X射线吸收率有关。从而，通过比较和计算，可以求出从A点到P点的平均X射线吸收率。令X射线源沿着圆周从A点移动到B点，发射的X射线将从B点穿过人体达到Q点。同样道理，可以计算求出从B点到Q点的平均X射线吸收率。于是，令X射线源沿圆周移动一圈，以不同的角度分别发射X射线穿透人体，就得到了无数的不同角度直线上的平均X射线吸收率。
从数学的角度来看，一根直线上的X射线平均吸收率就相当于在该直线上对于吸收率函数的积分值。因此，如果能根据函数在直线上的积分值来求出函数在各点的值，那么就可以实现CT的功能了。而这正是柯马克在1963年的那篇论文中所完成的工作。
其实，早在1917年，奥地利数学家拉东（Johann Radon, 1887-1956）就发表过一篇论文，其中提出，对于一个定义在一定区域上的函数f，如何从该函数在以不同角度穿过该区域的直线上的积分值，来求得其分布解的变换方法。这个方法后来被称为拉东变换。
设定义在平面区域D上的函数f(x,y)，穿过D和坐标原点的一根直线L的参数方程(x,y)=t(sin(α),-cos(α))+s(cos(α),sin(α))，其中α是L与x轴的夹角。则f的拉东变换为[5]。
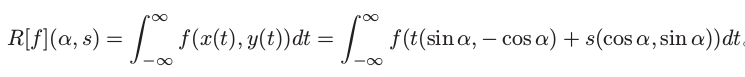
f的分布解可通过对R[f]进行逆变换得到。
柯马克的工作其实就是重新发现拉东变换，并把它用于放射医学问题。
CT技术的数学理论有着广泛的应用。例如，当用γ射线、质子或正电子带替X射线时，就相应得到了γ射线、质子或正电子的CT。这些CT图像有着不同于X射线图像的意义。比如说，正电子CT(PET)能够提供病人体内新陈代谢水平的分布图像。此外，该理论还可以用于其他领域，如测量海水温度分布、观察天体运动，等等。近几年有报道，CT技术被用于木材的无破坏内部检测，它将大大提高木材的利用率并降低生产成本。
参考文献和资料来源：
[1] O. 莱赫托. 数学无国界——国际数学联盟的历史. 王善平译. 上海：上海教育出版社，2002.
[2] 诺贝尔奖官方网站. http://nobelprize.org.
[3] Wikipedia. Allan McLeod Cormack. http://en.wikipedia.org/wiki/Allan_McLeod_Cormack.
[4] A. M. Cormack. Representation of a function by its line integrals, with some radiological applications I, II. Journal of Applied Physics, 1963, 34(9): 2722-2727; 1964, 35(10): 2908-2913.
[5] Wikipedia. Radon Transform. http://en.wikipedia.org/wiki/Radon_transform.
延伸阅读：
丘成桐. 3D改变未来. 数理人文杂志, Vol. 5, 2015年7月.
顾险峰. 共形几何在工程和医学实践中的一些应用. 数学与人文, Vol. 18, 2015年7月.
季理真. Why is there No Nobel Prize in Mathematics? ICCM Notices, 1(1), 42-52, 2013.
本文选自“数学与人文”第一辑，由“数学与人文“编辑组授权转载。
来源：数理人文
编辑：杨发枝
近期热门文章Top10
↓ 点击标题即可查看 ↓
1. 如果再读一次研究生
2. 13张图，带你认识大学各专业
3. 你以为你很懂水？
4. 拿过奥运会奖牌的数学家，数学博士答辩时却坐满了他的球迷
5. 磁场的本质是什么？|No.32
6. 广义相对论和狭义相对论的根本区别 |No.31
7. 物理天才马约拉纳消失之谜
8. 研究量子场论的 也许是这个星球上最聪明的一群人
9. 他是中科院超牛的物理学者，更是摇滚界无人不知的“李白”
10. “逗妹纸”的16种用法 | 线上科学日
点此查看以往全部热门文章
