通过大尺寸的量子多体热力学与动力学计算，来自北航、复旦、中科院物理所和香港大学的研究团队，成功“破译”了二维阻挫磁性晶体TmMgGaO4 (TMGO) 的“材料基因”—— 三角晶格量子伊辛模型及其精确模型参数。籍此，研究者预言指出，磁性晶体TMGO将在特定的温度范围内展现出Kosterlitz-Thouless (KT) 相。此前人们在二维超流和超导中观察到KT相变，而此项理论工作首次在实际二维磁性晶体中预言了KT物理的存在。通过分析自旋谱发现了三角晶格反铁磁体中存在类似超流体中的旋子激发，并解释为条纹反铁磁序竞争失败后留下的“幽灵软模”，团队结合赝自旋映射阐明了TMGO磁性晶体中旋子的拓扑起源 。
相关工作于2020年2月28日以“Kosterlitz-Thouless Melting of Magnetic Order in the Triangular Quantum Ising Material TmMgGaO4” 为题在线发表于综合学术期刊《自然·通讯》(Nature Communications) [1]。
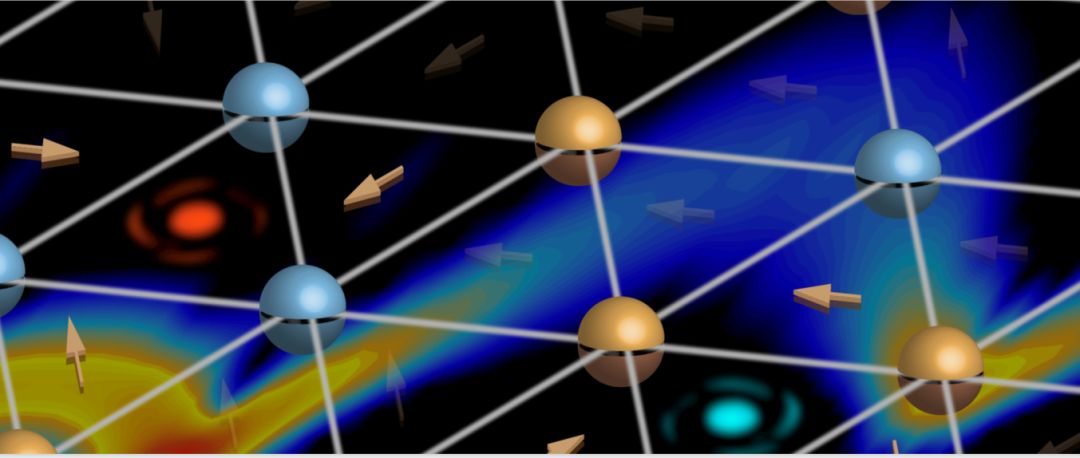
图 1 磁性晶体TMGO中的自旋织构与磁振子—涡旋对激发
阻挫反铁磁晶体是一类非常有趣的关联量子材料，丰富的多体效应使得其中涌现出新奇的量子物态与相变，不断吸引着人们在其中探寻凝聚态物理的新范式。在阻挫反铁磁中，由于存在强关联效应和磁有序的激烈相互竞争，开展精确理论计算并与实验对比仍然是亟待解决的前沿问题。在这项研究中，通过结合张量重正化群与量子蒙特卡洛方法等多体计算方法，开展了关联量子晶体材料的热力学—动力学的多体研究范式。揭示出反铁磁TMGO晶体的“材料基因”——量子伊辛微观模型及其精确模型参数，弥补了前期工作中的不足。如图2所示，通过指数张量重正化群计算，研究团队发现了一套正确的微观参数，可以在很宽的温度范围内完美地拟合实验观测 [2，3]的磁比热、熵曲线、磁化率、磁化曲线等诸多磁热力学性质。同时，采用这套参数进行的量子蒙卡动力学计算与实验自旋谱 [3]的直接比较也得到完全吻合的结果(图4(a))。因此，通过全方位、精确的关联量子材料模拟，确认TMGO晶体是一个研究多体涌现现象与物理的理想量子材料实验平台。图2 热态张量网络多体计算精确拟合 TMGO磁热力学测量数据尤为引人入胜的是，磁性晶体TMGO实现的是一个形式简单但内涵十分丰富的阻挫三角晶格横场伊辛模型。而精确定出的参数使得TMGO晶体处于令人感兴趣的包含KT相的区间内(图3(c))。在这个参数区间内，TMGO存在一种特殊的反铁磁序，“钟态有序”(clock order，图3(a))，被量子涨落所挑选出来成为基态，而另一个三角晶格反铁磁的有力竞争者“条纹序”(stripe order，图3(c))在低温不被相互作用所选择。然而，条纹序虽然不能实现在零温稳定的“存活”，但可以在自旋谱的中段能量区间留下幽灵般的痕迹——它们被称为旋子，对应很大的态密度。这些幽灵在比较低的温度下(～1 K)被大量激活，TMGO材料发生下临界KT相变，融化反铁磁序。随后系统进入一种类似两维超流态的奇特磁性“液体”状态，即著名的 KT相。
超流体中的旋子激发是一个非常有趣的问题，自朗道的唯象理论提出后 [4]，吸引了费曼、昂萨格等诸多著名物理学家来建立旋子的微观量子理论。昂萨格指出旋子代表超流体中涡管的“幽灵”(The Ghost of a Vanished Vortex Ring) [5]；费曼认为旋子对应着量子化的涡旋运动，旋子激发极小点对应着液态结构因子的极大点[6]；较为近代的观点认为，超流体旋子激发是近邻固体序竞争导致的软模 [7]，并在冷原子实验中被多次观察到。在TMGO固态材料研究中，如图4所示，自旋谱上清晰的看到，沿着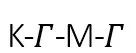
线，在布里渊区的M点附近存在一个平方色散的极小点，与超流旋子类似，称为自旋系统的旋子激发。全局来看，M点是一个鞍点，使得M旋子具有很大的态密度，这些与条纹反铁磁序关系密切的残存“幽灵”粒子，随温度升高其能隙逐渐降低、软化(图4(d))。特别地，M旋子在靠近上KT相变附近时急剧软化，但和通常意义下的软模不同，并不对应某种具体的对称性恢复，所以从这个意义上TMGO中的M旋子的确是一种奇特的“幽灵软模”。
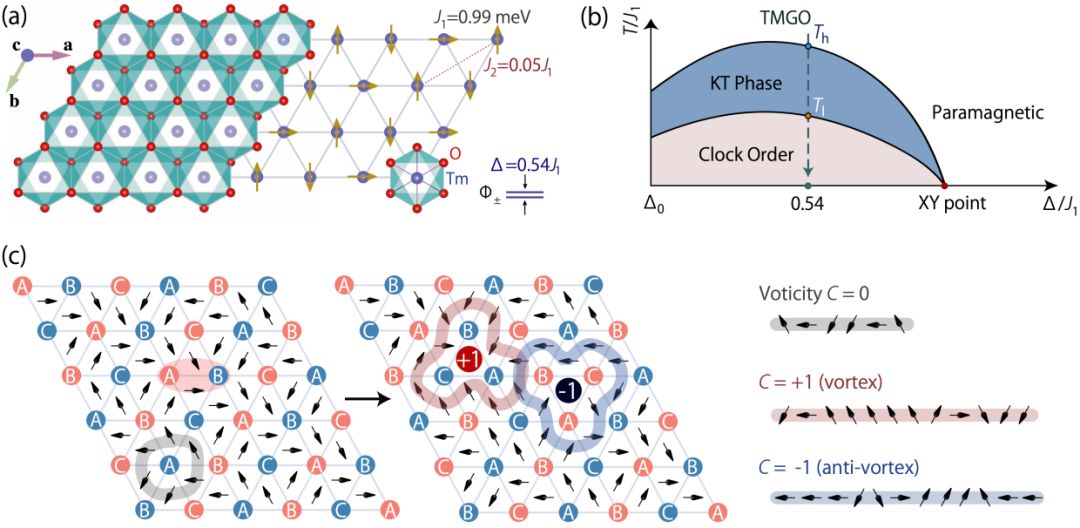
图 3 (a) TMGO晶体结构及钟态有序示意图；（b）热力学相图；（c）条纹状有序、赝自旋映射、自旋翻转与涡旋对激发图像
在KT相中，如图4(c)所示M旋子和无能隙长波磁振子激发一道，沿着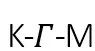
线，构成了类似于超流体的声子—旋子谱（著名的朗道能谱）。事实上，这些幽灵软模确实和旋转有关，通过赝自旋映射，研究发现鞍点附近的幽灵模式对应着涡旋—反涡旋对激发(图3(c))。在KT相中，系统演生出连续U(1)对称性，对应一个复序参量（赝自旋），并存在相位的（准）长程相干性（“超流序”）。在条纹反铁磁自旋织构的基础上，自旋的翻转激发会在赝自旋图像上激发一对涡旋(图3(c))。当温度超过上KT相变温度时，系统中的涡旋—反涡旋被拆散，发生十分有趣的拓扑相变，提供给系统破坏“超流序”的独特涡旋缺陷。随着涡旋等激发的数目激增，系统从可以类比于超流的“液态” 自旋KT相最终进入人们所熟悉的高温“气态”顺磁。图 4 二维自旋阻挫量子磁体 TMGO的量子多体蒙特卡洛动力谱学模拟结果。(a), (c), (d) 运用了正确的微观模型参数；(b)为之前工作中不准确的参数结果，在本团队的研究工作中得到了纠正综上，量子晶体TMGO提供了十分理想的实验平台，供人们研究有着丰富多体物理涌现性质的三角横场伊辛模型 。例如，可以通过进一步测量热力学数据在实验上得到系统的一些普适反常标度指数；通过动力学测量来探测二维磁性系统中的KT相，以及其中无耗散等“超流特性”的对应磁学性质等。因此，此项研究为进一步深入探讨二维量子磁性晶体TMGO提供了坚实的理论基础，并做出了若干进一步的实验预言。此外，对TMGO的研究同时也展示了综合平衡态与动力学多体计算开展精确研究关联量子晶体材料的新范式。北京航空航天大学博士生李涵（第一作者）和陈斌斌采用李伟课题组提出的指数张量重正化群方法[8]开展大规模模型热力学性质计算，与实验对比寻找到TMGO的精确模型参数。另一位第一作者为中科院物理研究所博士生廖元达，他采用物理所团队开发的量子蒙特卡洛＋随机解析延拓方法，开展了大尺寸动力学计算[9]，确认了模型计算可以精确重复出实验观察的动力学数据。复旦大学戚扬、中科院物理所和香港大学孟子杨与北航李伟分别围绕有效场论、自旋谱学和热力学性质对问题开展研究，并列为论文的通讯作者。北航硕士研究生曾旭涛和胜献雷助理教授对TMGO晶体开展了密度泛函计算与分析，为论文共同作者。
致谢： 本工作获得科技部重点研发计划(批准号：2016YFA0300502)，中科院先导专项(批准号：XDB28000000)，国家自然科学基金委(批准号：11421092, 11574359,11674370, 11974036, 11874115, 11834014)，以及香港特别行政区研究资助局 (批准号：17303019)和北航卓越百人计划、北航青年拔尖人才支持计划等项目资助。研究所进行的大规模并行计算，在中科院物理所量子模拟科学中心、国家超级计算天津中心的天河一号平台、国家超级计算广州中心天河二号平台上进行。研究团队特别感谢国家超算天津中心应用研发部孟祥飞部长、菅晓东工程师，国家超算广州中心应用推广部王栋部长、崔颖妍工程师等人的有力支持和配合。
孟子杨，中科院物理所研究员，香港大学副教授。发展和运用量子蒙特卡洛计算方法，研究凝聚态物理量子多体问题中的相变与临界现象。发表论文80余篇。获DFG (Deutsche Forschungsgemeinschaft, German Research Foundation, 德国研究基金) Mercator Fellow 奖项。国家超算中心颁发的“天河应用创新卓越奖”。
戚扬，复旦大学研究员，主要研究强关联电子系统理论、拓扑序、量子相变等量子多体现象，以及用数值模拟方法研究量子多体系统。2005年于清华大学物理系获学士学位，2010年美国哈佛大学物理系获博士学位，随后在清华高研院、加拿大理论物理圆周研究所、美国麻省理工学院从事博士后和访问教授研究工作等。
李伟，北航副教授，本科物理专业“固体物理学”主讲教师。2006年本科毕业于北航，2011年博士毕业于中国科学院大学，2012年-2015年在德国慕尼黑大学从事博士后科研工作，随后回到北航工作。研究方向为量子多体理论、张量重正化群方法等，发表论文40余篇。曾获中国科学院优秀博士学位论文奖等。
参考文献
[1] Han Li, Yuan Da Liao, Bin-Bin Chen, Xu-Tao Zeng, Xian-Lei Sheng, Yang Qi, Zi Yang Meng, and Wei Li, “Kosterlitz-Thouless Melting of Magnetic Order in the Triangular Quantum Ising Material TmMgGaO4”, Nature Communications, 11, 1111 (2020).[2] Y. Li, S. Bachus, H. Deng, W. Schmidt, H. Thoma, V. Hutanu, Y. Tokiwa, A. A. Tsirlin, and P. Gegenwart, “Partial up-up-down order with the continuously distributed order parameter in the triangular antiferromagnet TmMgGaO4,”
Phys. Rev. X 10, 011007 (2020).
[3] Y. Shen, C. Liu, Y. Qin, S. Shen, Y.-D. Li, R. Bewley, A. Schneidewind, G. Chen, and J. Zhao, “Intertwined dipolar and multipolar order in the triangular-lattice magnet TmMgGaO4,” Nat. Commun. 10, 4530 (2019).[4] L. Landau, “On the theory of superfluidity,”Phys. Rev. 75, 884–885 (1949).
[5] R. J. Donnelly, “The ghost of a vanished vortex ring,” in Quantum Statistical Mechanics in the Natural Sciences: A Volume Dedicated to Lars Onsager on the Occasion of his Seventieth Birthday, edited by S. L. Mintz and S. M. Widmayer (Springer US, Boston, MA, 1974) pp. 359–402.
[6] R. P. Feynman, Progress in Low Temperature Physics: Chapter II, Application of Quantum Mechanics to Liquid Helium, edited by C. G. Gorter, Vol. 1 (North Holland, 1955).
[7] P. Nozieres, “Is the roton in superfluid He4 the ghost of a Bragg spot?” J. Low Temp. Phys. 137, 45–67 (2004). [8] Bin-Bin Chen, Lei Chen, Ziyu Chen, Wei Li, and Andreas Weichselbaum, “Exponential Thermal Tensor Network Approach for Quantum Lattice Models”, Phys. Rev. X 8, 031082 (2018).[9] Nvsen Ma, Guang-Yu Sun, Yi-Zhuang You, Cenke Xu, Ashvin Vishwanath, Anders W. Sandvik, and Zi Yang Meng, “Dynamical signature of fractionalization at a deconfined quantum critical point”, Phys. Rev. B 98, 174421 (2018) Editors' Suggestion
1.无悔的岁月 永远的芳华——追忆著名女物理学家李方华先生
2.濒危元素
3.皮布尔斯的物理宇宙
4.量子多体中的呐喊与彷徨
5.锂离子电池过往与未来
6.百年物理诺奖回顾：我们的崇敬与误解
7.钻石中的量子达尔文主义
8.爱德华·威滕：基础物理学的重大变革会在哪里？
9.桃李满天下为大师之师 无缘于诺奖成无冕之王
10.从流浪地球到宇宙迷航——2019年诺贝尔物理学奖解读
