数理统计和KPI之间的千丝万缕

在数据分析师的圈子里，有好多初来的新手都会问这样一个问题：数据分析方法论中，数理统计那么难，在实际应用中到底有没有用？或者能用上多少？我看过很多留过洋的老司机对国外数理统计的实用性的评价都已经到了骨灰级的程度，而很多本土的老司机们也都有他们应用方面的实战故事。

这里我就也简单装下门面，举两个例子来说明下，看看能否对大家有帮助。

一、“中心极限定理”应用于指标间的量纲差异消除

还记得那会儿是初入职场不久的时候，有一天我的主管和我说，隔壁 J 部门的营销 KPI 管理职能划到咱部门了，让我对现行的 KPI 管理的方法做一个审视，然后拟一套新的出来。

末了我主管还加上一句“好好干，我相信你一定可以的。但别搞太复杂，到时候方案还要上事业部总经理会议做最后审批的。要是搞太复杂的话就你自己上去讲啊！”

哎呦我的妈呀，画的好香的一张饼和好怕人的一个紧箍咒啊！在这里我就不再详述当时仿佛端着一碗水过洪水中的独木桥那紧张心情了。

我记得当时修改了好几个地方，但有一点我印象最深刻：那就是指标之间的加权叠加改良。说实话，这件事放到现在来看，真的是感觉很小菜一碟，但那个时候一个大公司里面居然有这种低级错误发生，觉得太不可思议了。

啥问题呢？那就是几个 KPI 的考核指标，他们的原始值加权平均时，居然不做任何处理！下面的表是当时的几个指标，大家看看就知道问题在哪儿了。

分析完上面的各个指标的特点后，我们举个例子大家看看我当时的前任，对潜在或显性问题有多严重的忽视程度：假设有 A 和 B 两个地市的销售公司，某月的各个营销 KPI 指标如下：

我们看到， B 分公司促销场数多，费用因此也高，但任务没完成，检查得分也很一般，可以说投入产出比并不见得好看。但 B 分公司却比 A 公司得分要高，就是因为促销场次多，促销得分增加速度非常快，增幅影响也非常大。因此，只要你狂搞促销，哪怕促销效果不太好，投入产出不高，但得分还是会比较有优势。你还别笑，这种事情就在我接手的当时发生着。

如果时间放到现在的话，你只要上网我相信能够百度出一堆的方法出来，用以规避这一些量纲问题。但我刚进入社会的那个年代，百度还没那么丰富的内容可以搜索。我于是应用的是数理统计中的 “ 列维 - 林德伯格 ” 中心极限定理来做的原始数据处理。具体的计算公式可见下面方：

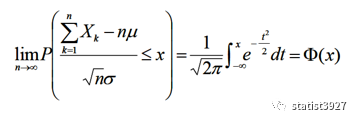
上面的中心极限定理在实用的过程中，有个非常有用的 “ 中心化 ” 过程：

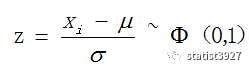
即 z 值服从标准正态分布。 其中

xi 为指标的原始值， n 为每个指标的样本个数。

这样做有什么优点呢？首先 z 值消除了数据的量纲差异，也就是说各个指标的变化幅度全部统一了，其次只要是正常能力范围内做到的事情，指标的映射 z 值出现的概率都不会低到哪里去；与此同时，你若真的有过人的天赋和过人的能力的话，指标的分数也足以拉开和众人的距离。

我记着广东省千禧年的高考还用这种标准分方法呢。不过如果熟悉标准正态分布的朋友您可能会担心， z 值有正有负，所以说届时大家得到负数分时会不会心理难接受啊。所以为了解决这个问题，我还是参考标准分法把它做了线性放大，这样就不会出现负数分了。方法如下：

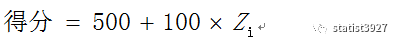
后来，我记得我把方法和主管做了说明以后，他还是用实际的数据试算了一把。看到结果很合乎他的预期后，又看了看我的方案，于是 他非常高兴地把向总经理介绍这个方案的任务交到了我手上！！

就这样过了几个忐忑的模拟演讲的夜晚，当我在会上把这个方案做了详细的解释之后，没想到老总竟然愉快的通过了我的方案！

再后来，过了几年在翻阅新成立的精品事业部的营销管理办法时，居然也用了我的这个思路，我当时那感觉真和“这 feel 倍爽”里的歌词一模一样呵。

二、随机游程检验预判指标的规律性

说到预测准确率，我想大家脑海里很容易就蹦出一个非常直觉得公式：偏差率。就是（预测值 - 实际值） / 实际值。它还有个亲兄弟即“准确率”： 1- 偏差率。

如果放眼望去，业界也有别的方法，比方说就有 MIN （实际，预测） /MAX （预测，实际）这种（以下简称 M ）。不久前我们还在一起开会讨论一个话题：那就是预测准确率的多种公式，哪种会好一点？

其实准确率的公式都是人定出来的，你说好跟差，实际上就是尽可能的看，谁更能反映预测或计划这个业务的能力要求。

这也不是我们第一次讨论他们的差异了，他们之间的差异确实也非常的清晰和简单。对于准确率的直观公式，唯一缺点就是变化幅度没有上下限，解释起来可能有些麻烦；而 M 的变化幅度为 [0 ， 1] 刚好可以修补这个 BUG 。

但 M 也存在其他问题。例如实际发生 100 ，但甲乙两人一个人预测 80 ，另个人预测 120 。偏差一样的情况下，前者准确率 80% ，后者准确率 83.33% ，后者准确率居然高于前者！

尽管之前我们看到了这样那样的问题，但本次我们讨论的是一个比较新的话题：直观准确率和 M 之间，会不会存在非随机问题。

如果这句话如果翻译一下的话，就是如果不是随机数，那么就有可能被预测，或找出规律。这样一来，是不是可能没那么努力也可以得到高分，或者说，再怎么努力也就只能这个分数上下？

就这个问题我于是按照最严苛的方式，假设某产品可能的订单数介于 [50 ， 10000] 之间，但预测跟实际发生都无法判断，我随机的生成了 2000 个预测值和 2000 个实际值，然后用这两种方法算出了各 2000 个准确率。（ 想要获取这2000个随机数序列，可以发邮件找我要。请发至[email protected] ）

于是我用非参数检验中的随机游程检验这 2000 个准确率，也就是 Npar test 做了测试。结果还真的让我大呼吃惊：