

说到公式,小编就头痛,小时候读书时,一大堆的公式真是难记,有数学公式,物理公式,化学公式,没有上千条,也是百上条,有些公式还十分相近,背这些公式真是十分伤脑筋的事情,但是每一个公式的出现都推动了科技的进步,每一个公式的发现都是先辈们付出了极大努力甚至是一生的努力的结果。这个地球上有多少伟大的智慧曾耗尽一生,才最终写下一个等号。每当你解不开方程的时候,不妨换一个角度想,暂且放下对理科的厌恶和对考试的痛恨。因为你正在见证的,是科学的美丽与人类的尊严。
今天就来和度哥世界之最网一起来看看世界上最伟大的十个公式。看完后你或许会发现这些东西原本如此美丽,如此精妙。
英国科学期刊《物理世界》曾让读者投票评选了“最伟大的公式”,最终榜上有名的十个公式既有无人不知的1+1=2,又有著名的E=mc2;既有简单的圆周公式,又有复杂的欧拉公式……欧拉公式你不知道吗?这可是被称为世界上最完美的公式,那么欧拉公式到底为什么被称为世界上最完美的公式了,下面就来跟随小编解开欧拉公式的神秘面纱吧。

世界上最伟大的十个公式:欧拉公式,麦克斯韦方程组,牛顿第二定律,牛顿第二定律,薛定谔方程,德布罗意方程组,傅立叶变换,圆的周长公式。
No.1 欧拉公式(Euler's Identity)

这个公式是上帝写的么?到了最后几名,创造者个个神人。欧拉是历史上最多产的数学家,也是各领域(包含数学的所有分支及力学、光学、音响学、水利、天文、化学、医药等)最多著作的学者。数学史上称十八世纪为“欧拉时代”。欧拉出生于瑞士,31岁丧失了右眼的视力,59岁双眼失明,但他性格乐观,有惊人的记忆力及集中力。他一生谦逊,很少用自己的名字给他发现的东西命名。不过还是命名了一个最重要的一个常数——e。
这个公式的巧妙之处在于,它没有任何多余的内容,将数学中最基本的e、i、pie放在了同一个式子中,同时加入了数学也是哲学中最重要的0和1,再以简单的加号相连。高斯曾经说:“一个人第一次看到这个公式而不感到它的魅力,他不可能成为数学家。”
虽然不敢肯定她是世界上“最伟大公式",但是可以肯定她是最完美的数学公式之一。
理由如下:
1。自然界的 e 含于其中。
自然对数的底,大到飞船的速度,小至蜗牛的螺线,谁能够离开它?
2。最重要的常数 π 含于其中。
世界上最完美的平面对称图形是圆。“最伟大的公式”能够离开圆周率吗?
(还有π 和e是两个最重要的无理数!)
3。最重要的运算符号 + 含于其中。
之所以说加号是最重要的符号,是因为其余符号都是由加号派生而来。减号是加法的逆逆运算,乘法是累计的加法……
4。最重要的关系符号 = 含于其中。
从你一开始学算术,最先遇见它,相信你也会同意这句话。
5。最重要的两个元在里面。
零元 0 ,单位 1 ,是构造群,环,域的基本元素。如果你看了有关《近世代数》的书,你就会体会到它的重要性。
6。最重要的虚单位 i 也在其中。
虚单位 i 使数轴上的问题扩展到了平面,而在哈密尔的 4 元数与 凯莱的 8 元数中也离开不了它。
之所以说她美,是因为这个公式的精简。她没有多余的字符,却联系着几乎所有的数学知识。
有了加号,可以得到其余运算符号;
有了0,1,就可以得到其他的数字;
有了 π 就有了圆函数,也就是三角函数;
有了 i 就有了虚数,平面向量与其对应,也就有了哈密尔的 4 元数,现实的空间与其对应;
有了 e 就有了微积分,就有了和工业革命时期相适宜的数学。
(3)三角形中的欧拉公式:
设r为三角形外接圆半径,r为内切圆半径,d为外心到内心的距离,则: d^2=r^2-2rr
(4)拓扑学里的欧拉公式:
v+f-e=x(p),v是多面体p的顶点个数,f是多面体p的面数,e是多面体p的棱的条数,x(p)是多面体p的欧拉示性数。
如果p可以同胚于一个球面(可以通俗地理解为能吹胀而绷在一个球面上),那么x(p)=2,如果p同胚于一个接有h个环柄的球面,那么x(p)=2-2h。
x(p)叫做p的欧拉示性数,是拓扑不变量,就是无论再怎么经过拓扑变形也不会改变的量,是拓扑学研究的范围。
在多面体中的运用:
简单多面体的顶点数v、面数f及棱数e间有关系
v+f-e=2
这个公式叫欧拉公式。公式描述了简单多面体顶点数、面数、棱数特有的规律。
(5)初等数论里的欧拉公式:
欧拉φ函数:φ(n)是所有小于n的正整数里,和n互素的整数的个数。n是一个正整数。
欧拉证明了下面这个式子:
如果n的标准素因子分解式是p1^a1*p2^a2*……*pm^am,其中众pj(j=1,2,……,m)都是素数,而且两两不等。则有
φ(n)=n(1-1/p1)(1-1/p2)……(1-1/pm)
利用容斥原理可以证明它。
此外还有很多著名定理都以欧拉的名字命名。
No.2 麦克斯韦方程组(The Maxwell's Equations)
积分形式:
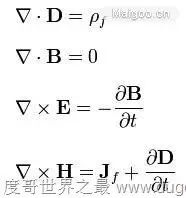
微分形式:

任何一个能把这几个公式看懂的人,一定会感到背后有凉风——如果没有上帝,怎么解释如此完美的方程?这组公式融合了电的高斯定律、磁的高斯定律、法拉第定律以及安培定律。比较谦虚的评价是:“一般地,宇宙间任何的电磁现象,皆可由此方程组解释。”到后来麦克斯韦仅靠纸笔演算,就从这组公式预言了电磁波的存在。我们不是总喜欢编一些故事,比如爱因斯坦小时候因为某一刺激从而走上了发奋学习、报效祖国的道路么?事实上,这个刺激就是你看到的这个方程组。也正是因为这个方程组完美统一了整个电磁场,让爱因斯坦始终想要以同样的方式统一引力场,并将宏观与微观的两种力放在同一组式子中:即著名的“大一统理论”。爱因斯坦直到去世都没有走出这个隧道,而如果一旦走出去,我们将会在隧道另一头看到上帝本人。
No.3 牛顿第二定律(Newton's Second Law of Motion)

有史以来最伟大的没有之一的科学家在有史以来最伟大没有之一的科学巨作《自然哲学的数学原理》当中的被认为是经典物理学中最伟大的没有之一的核心定律。动力的所有基本方程都可由它通过微积分推导出来。对于学过高中物理的人,没什么好多讲了。
No.4 勾股定理/毕达哥拉斯定理(Pythagorean Theorem)

做数学不可能没用到过吧,不多讲了。
No.5 质能方程(Mass–energy Equivalence)
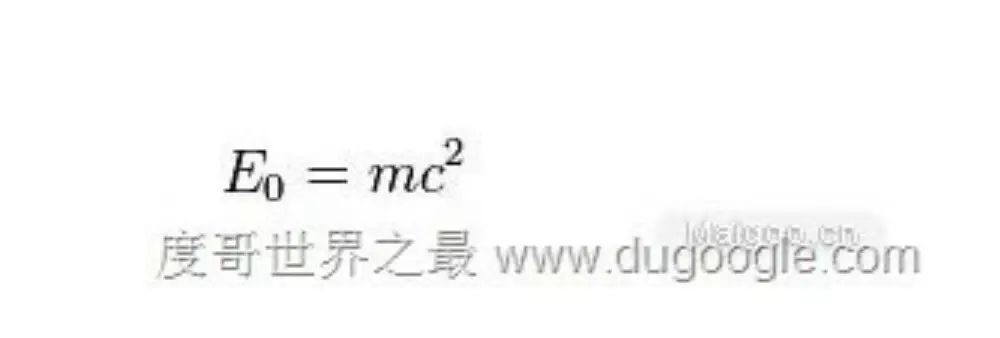
好像从来没有一个科学界的公式有如此广泛的意义。在物理学“奇迹年”1905年,由一个叫爱因斯坦的年轻人提出。同年他还发表了《论动体的电动力学》——俗称狭义相对论。这个公式告诉我们,爱因斯坦是挺NB的,能量和质量是可以互换的。副产品:原子弹。
No.6 薛定谔方程(The Schrödinger Equation)
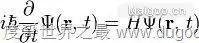
也是一般人完全不明白的。因此我摘录官方评价:“薛定谔方程是世界原子物理学文献中应用最广泛、影响最大的公式。”由于对量子力学的杰出贡献,薛定谔获得1933年诺贝尔物理奖。另外薛定谔虽然姓薛,但是奥地利人。
No.7 1+1=2
这个公式不需要名称,不需要翻译,不需要解释。
No.8 德布罗意方程组(The de Broglie Relations)

高中物理学到光学的话很多概念跟它是远亲。简要地说德布罗意这人觉得电子不仅是一个粒子,也是一种波,它还有 “波长”。于是搞啊搞就有了这个物质波方程,表达了波长、能量等等之间的关系。同时他获得了1929年诺贝尔物理学奖。
No.9 傅立叶变换(The Fourier Transform)
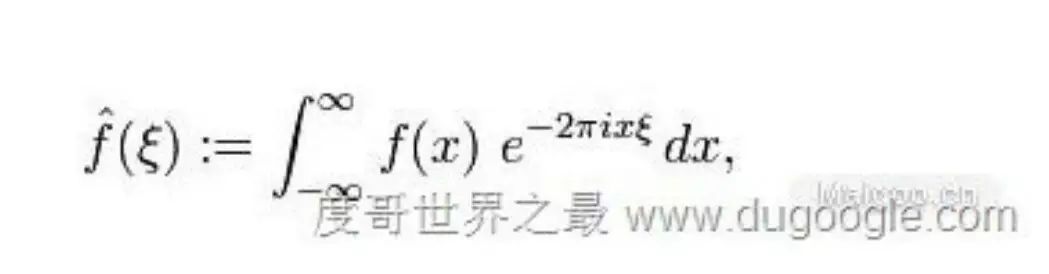
这个挺专业的,一般人完全不明白。不多作解释。简要地说没有这个式子没有今天的电子计算机,所以你能在这里上网除了感谢党感谢政府还要感谢这个完全看不懂的式子。另外傅立叶虽然姓傅,但是法国人。
No.10 圆的周长公式(The Length of the Circumference of a Circle)

目前,人类已经能得到圆周率的2061亿位精度。现代科技领域使用的圆周率值,有十几位已经足够了。如果用35位精度的圆周率值,来计算一个能把太阳系包起来的一个圆的周长,误差还不到质子直径的百万分之一。现在的人计算圆周率,多数是为了验证计算机的计算能力,还有就是为了兴趣。
当然,世界上除了这最伟大的十个公式外,还有许多的公式值得大家记住他们,让我们向伟人们表示敬意。

གཞིས་རྩེའི་དྲ་ཐོག
 点击“阅读原文”,即可查看“视频”,也可寻找你想要的更多内容。。。
点击“阅读原文”,即可查看“视频”,也可寻找你想要的更多内容。。。


















