
这次
我真的懂了
之前,超模君跟大家分享了
10张劲爆眼球的科学动图(
传送门
),最后压轴的
无限雪花
吸引了无数的“雪花粉”。


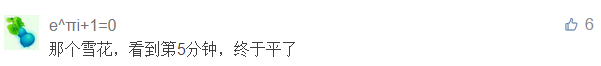


无限雪花其实
分形
的一种表现——
Koch(科赫) 曲线。
“
分形
Fractal
”,
是
曼德勃罗与1975年
创造出来的,其原意就是指不规则、破碎等,
曼德勃罗
想用这个词来描述自然界中传统欧几里德几何学所不能描述的一大类
复杂无规
的几何对象
。
这些几何对象
具有
自相似
的性质,即他们
可以分成数个部分,而每一部分都是整体缩小后的形状,就像上图的无限雪花那样。
那这样的曲线是怎样画出来的呢?
首先画一个线段,然后把它平分成三段,去掉中间那一段并用两条等长的线段代替。这样,原来的一条线段就变成了四条小的线段。用相同的方法把每一条小的线段的中间三分之一替换为等边三角形的两边,得到了16条更小的线段。然后继续对16条线段进行相同的操作,并无限地迭代下去。。。
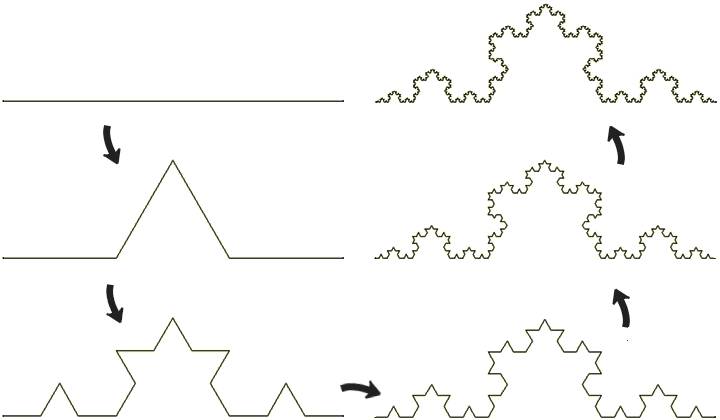


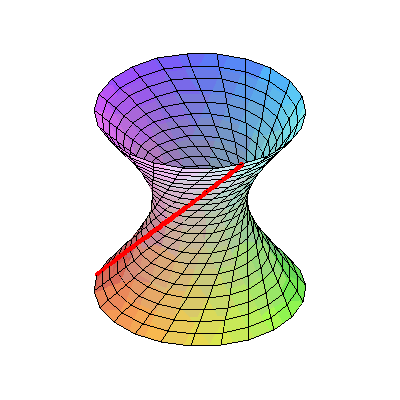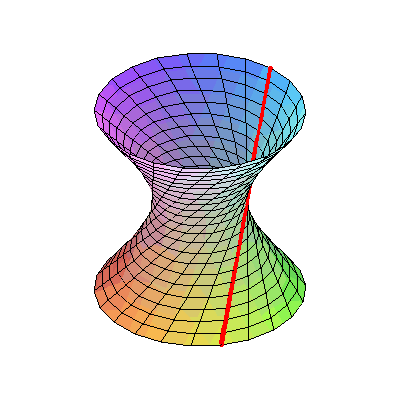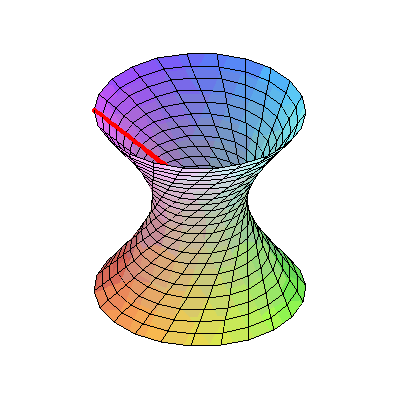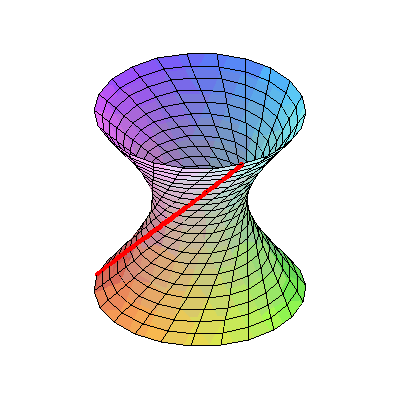
当你看到这张动图的时候,有没有这个疑惑:这根直杆为什么能从弯曲的洞里穿过?
其实很简单,
这根杆是
斜着
的,杆中间的点离旋转轴最近,因此对应的洞上的点离旋转轴也最近;杆两边的点离旋转轴比较远,与之对应的洞上的点离旋转轴就远。所以,能让这根杆通过的肯定不会是直线,只会是一条曲线,而且是双曲线。
实际上,这根斜着的杆旋转出来的面是一个
单叶双曲面
。

关于圆面积公式的推导,开普勒大胆地把圆分割成无穷多个小扇形,并果敢地断言:无穷小的扇形面积,和它对应的无穷小的三角形面积相等,而圆面积就等于无数个小扇形的面积和。
类似地,我们可以把圆
拆成无限个同心的细圆环,
然后,把这些圆环展开,就变成一个高为 r,底边长为 2πr 的三角形,于是,
S = 1/2·r ·
2πr =
πr
2
当然,这谈不上是严谨的证明,但其中已经蕴含了一些微积分的思想。我们甚至可以利用类似于古希腊穷竭法的办法,把它写成一个相对严谨的证明。

图片来源:Hyrodium's Graphical MathLand
球的体积公式的推导用到了
祖暅
(gèng)
原理。
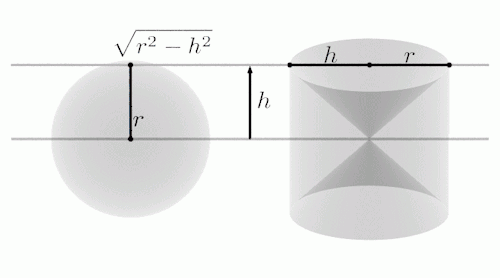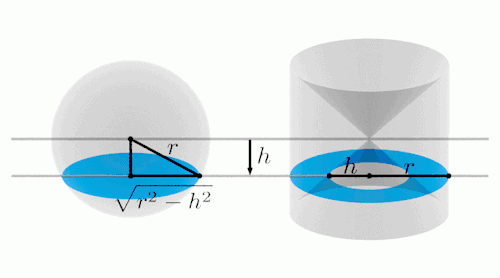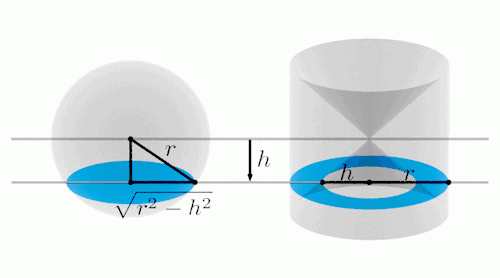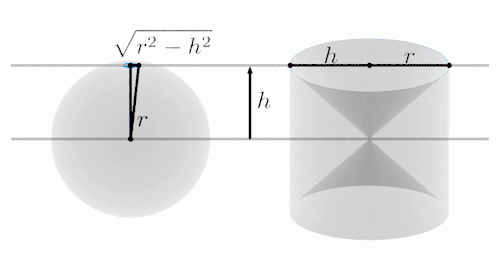
祖暅原理,又名等幂等积定理、卡瓦列里原理,是指夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任何平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等。
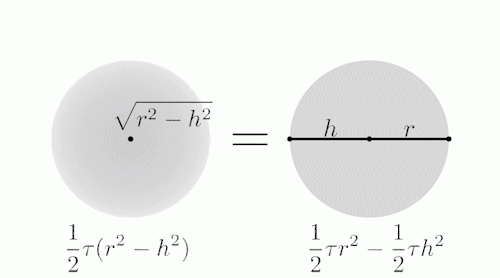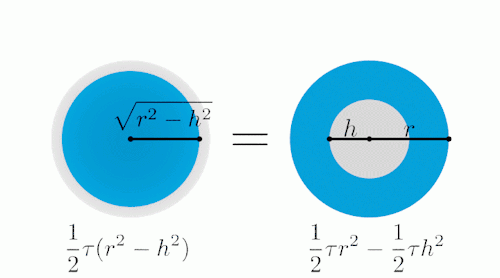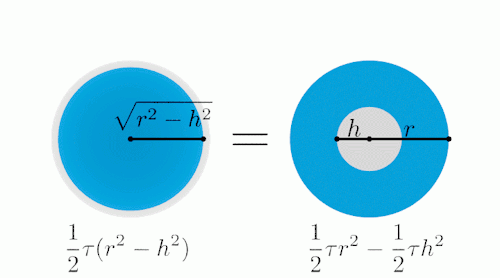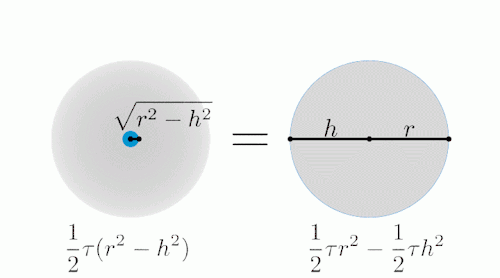
由上面的动图可以看出,我们从
底面半径为r、高为2r的圆柱体挖去两个高为r的圆锥,所得到的剩余部分
与半径为r的球体进行逐层比较,
你会发现二者在每个高度上的截面积都是相等的。
就这样,球体的体积等是圆柱与两个圆锥的体积之差:
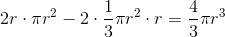
这相当于高等数学中的
二重积分能够通过逐次积分来计算,
可以看成是微积分的一个“前奏”。
在17世纪上半叶,意大利数学家卡瓦列里提出了这条原理,并用它计算了一系列几何体的体积,而在17世纪下半叶,牛顿和莱布尼兹发明了微积分。。。

其实,早
在公元5世纪,
祖暅
(
祖冲之的儿子
)
在求球的体积公式的过程中就提出了这条原理,
比卡瓦列里早了至少1100年。但他还不是第一个算出球体积公式的人。
第一个算出球体积公式的人是
古希腊的阿基米德,
在公元前3世纪,
他用一种奇妙的力学方法,算出半径为r的球体积是半径为r、高为2r圆柱体积的
2/3
,并用穷竭法给出了证明。
阿基米德的方法
已经有了微积分思想的雏形。

 最后,在这美好的周末,超模君送模友一份
无限巧克力
吧!
最后,在这美好的周末,超模君送模友一份
无限巧克力
吧!

本文由超级数学建模编辑整理
部分资料来源于网络
转载请在公众号中,回复“转载”
-----这里
是数学思维的聚集地------
“
超级数学建模
”(微信号
supermodeling
),
每天学一点小知识,轻松了解各种思维,做个好玩的理性派。30万数学精英都在关注!

↓
↓
↓
《
超级数学建模官方旗舰店
》已上线,赶紧来团!





