文章主要介绍了通过折纸方法确定正方形一边上的一个三等分点的操作过程及证明，并涉及两个小组的不同操作方法和思路。同时，文章还涉及一本名为《中考压轴专题》的书及其内容更新和增加的部分。
文章中介绍了通过折纸方法确定正方形一边上的三等分点的操作过程，包括乘风小组和破浪小组的不同操作方法，以及证明过程。
文章提及了《中考压轴专题》这本书，并介绍了其包含的专题和题型，以及最近的更新和增加的内容，包括解决几何最值问题的核心技巧和平面几何综合压轴题等。
文章认为题目篇幅较长，有偏离数学简洁美的风险，建议减小篇幅，避免将简单问题复杂化。同时，强调了精准训练和提升解题能力的重要性。
(
南山育才
)
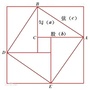
【综合与实践】在一次综合实践活动课上，王老师给每位同学各发了一张正方形纸片，请同学们思考如何仅通过折纸的方法来确定正方形一边上的一个三等分点
.
【操作探究】
“
乘风
”
小组的同学经过一番思考和讨论交流后，进行了如下操作：
第
1
步：如图
1
所示，先将正方形纸片
ABCD
对折，使点
A
与点
B
重合，然后展开铺平，折痕为
EF
；
第
2
步：将
BC
边沿
CE
翻折到
GC
的位置；
第
3
步：延长
EG
交
AD
于点
H
，则点
H
为
AD
边的三等分点
.
证明过程如下：连接
CH
，
∵正方形
ABCD
沿
CE
折叠
∴∠
D=
∠
B=
∠
CGH=90
°，
_______,
又∵
CH=CH
∴△
CGH
≌△
CDH
∴
GH=DH
由题意可知
E
是
AB
的中点，设
AB=6
，
DH=
x
，则
AE=BE=EG=3
，
在
Rt
△
AEH
中，可列方程：
_______
解得：
DH=______,
即
H
是
AD
边的三等分点
.
“
破浪
”
小组是这样操作的：
第
1
步：如图
2
所示，先将正方形纸片对折，使点
A
与点
B
重合，然后展开铺平，折痕为
EF
；
第
2
步：再将正方形纸片对折，使点
B
与点
D
重合，再展开铺平，折痕为
AC
，沿
DE
翻折得折痕
DE
交
AC
于点
G
；
第
3
步：过点
G
折叠正方形纸片
ABCD
，使折痕
MN||AD.
【思考过程】
(1)
“乘风”小组的证明过程中，三个空所填的内容分别是
______; _______; _______;
(2)
结合“破浪”小组的操作过程，判断点
M
是否为
AB
边的三等分点，并证明你的结论：
【拓展提升】
(3)
如图
3
，在菱形
ABCD
中，
AB=5
，
BD=6
，
E
是
BD
上的一个三等分点且
DE
连接
AE
，使点
D
关于
AE
的对称点为
D´,
连接
ED´
并延长与菱形
ABCD
的边交于点
F
，并依照上述描述在图
3
中将图补全，并直接写出
D´F
的长
_______
解：
(1)CG=CD,
,2
(2)
证明：延长
DE
交
CB
延长线于点
H
，易知
△ADE≌△BHE
，得
BH=AD
，
AD:CH=1
：
2
，故
AG:GC=1:2
，而
MG||BC
，得
AM
：
MB=1
：
2,
即
M
为
AB
的三等分点；
(3)
如图，易知
△
EMD
´
~
△
EFB
得
，得
EF=2EM
，设
EM=m
，则
EF=2m
，
BM=4-m
同时
△
MED
´
~
△
MAB
，得
，得
AM=
，
MD
´
=
,
AD
´
=5,
即
=5,
得
m=
，
D
´
F=
点评：题目篇幅有点长，但是立足点仍然是几何证明及求解，从全等至相似，从正方形到菱形，难度上有一定的梯度，有一定的探究性.建议减小题目篇幅，否则有些偏离了数学的简洁美，将简单问题复杂化，走偏的风险在增加.
2025版来了！经过了不断的积累和沉淀，不断对中考数学题型的研究与总结，《中考压轴专题》隆重推出，帮助同学们提升实力.本书包含6个大专题，每个专题下包含多个考点和题型，力求覆盖所有压轴题型.题目取自中考真题、平时模拟真题中的压轴题、经典题，可帮助同学们精准训练，提升解题能力.
2025版《中考压轴》经历了较长时间的修订，专题一增加了《解决几何最值问题的核心技巧》,帮助同学们站得更高，确保拿下此类题型.
增加了《平面几何综合压轴25题》,题目源自2024中考真题及模拟题，经历反复推敲和选择确定.
中考真题经典系列，增加了2024年各地中考及模拟题中的填空及选择题压轴，作为平时的练习题.
