1. GMM 简介
广义矩估计 ( Generalized Method of Moment , 简称 GMM ) 是一种构造估计量的方法，类似于极大似然法 ( MLE ) 。MLE 通过假设随机变量服从特定的分布，进而将待估参数嵌入似然函数，通过极大化联合概率密度函数得到参数的估计值。GMM 则是以随机变量遵循特定矩的假设，而不是对整个分布的假设，这些假设被称为矩条件。这使得 GMM 比 MLE 更稳健，但会导致估计量的有效性有所降低 (估计出的标准误比较大)。
2. MM 估计量
其中， N 表示样本数，
表示 y 的第 i 个观察值 。此处，估计量
被称为矩估计量( the method of moments estimator )，简称 MM 估计量。这是因为，该估计量的构造以母体矩条件( population moment condition )为基础，进而用其样本矩条件（依赖于我们使用的数据）做等价代换。因为我们从总体矩条件开始，然后运用类比原理得到一个依赖于观测数据的估计量。
2.1 PMC 和 SMC 样本均值的估计
我们想要估计随机变量 Y 的均值，即
，其中“母体矩条件( PMC )”为：
为从这个母体中随机抽取的一组样本观察值，则对应的“样本矩条件( SMC )”为
因此，我们可知母体矩条件的样本均值估计为：
，样本矩条件的样本均值估计为：
。
例子：
自由度为 k 的
随机变量的均值为 k ，方差为 2k ，因此两个母体矩条件( PMC )如下：
这个母体中随机抽取的一组样本观察值
，对应的样本矩条件( SMC )为：
2.2 MM 估计的一般形式
矩估计法是用样本的 k 阶矩作为总体的 k 阶矩的估计量，建立含待估计参数的方程，从而可解出待估计参数。
一般地，不论总体服从什么分布，总体期望
与方差
存在，则根据据估计法，它们的矩估计量分别为：
2.2.1 OLS 估计
OLS 估计可以视为矩估计的一个特例。OLS 估计的公式为：
其中，
与
不相关，则有
。因此，
其中
是母体矩条件，对应的样本矩条件为：
求解即可得到 OLS 估计下的
。
2.2.2 IV 估计
工具变量法（IV）是为了解决一个违反经典假设问题而设计的，假设条件是：解释变量与随机扰动项不相关。如果出现了违反该假设的问题，就需要找一个和解释变量高度相关的、同时和随机扰动项不相关的变量。
要注意的问题是，工具变量的设定除了上述两个条件以外，工具变量的个数至少要大于或者等于解释变量的个数，常数项是默认的工具变量，和随机扰动项不相关的解释变量也可以作为工具变量。工具变量是矩估计的一种形式。
假设公式为：
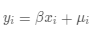，根据公式可得：
，
取得工具变量为
，其中
，
得到
，则
，
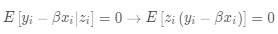为母体矩条件，
对应的样本矩条件为：
，
求解即可得到工具变量估计下的
。
3. GMM
3.1 为何要使用 GMM ？
GMM 估计中，假设待估参数的个数为 k ，矩条件的个数为 l ：
1.恰好识别( just or exactly identified )：当 k = l 时，即待估参数个数等于矩条件个数；2.过度识别( overidentified )：当 k < l 时，即待估参数个数小于矩条件个数。
GMM 是矩估计（ MM ）的推广。在恰好识别情况下，目标函数的最小值等于 0 ，GMM 估计量与 MM 估计量等价；然而在过度识别情况下，MM 不再适用，GMM 可以有效地组合矩条件，使 GMM 比 MM 更有效。
在 GMM 估计中，母体矩条件为：E[y]-u=0 ，
样本矩条件为：
，
通过求解样本矩条件得到 GMM 均值估计：
。
3.2 两阶段最小二乘法
两阶段最小二乘法其本质上是属于工具变量，回归分两个阶段进行，因此而得名。具体机理是：
第一步，将结构方程先转换为简化式模型（约简型方程），简化式模型里的每一个方程都不存在随机解释变量问题，可以直接采用普通最小二乘法进行估计。
第二步，由第一步得出的
的估计量替换 Y 。该方程中不存在随机解释变量问题，也可以直接用普通最小二乘法进行估计。
例子：一般 IV 回归模型为：
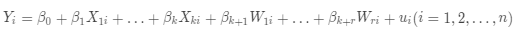(a)
其中：
-
为因变量；
-
为误差项，表示测量误差和/或遗漏因素；
-
表示k个内生回归变量，可能与
相关；
-
表示 r 个包含的外生变量，与
不相关；
-
为未知回归系数；
-
为 m 个工具变量。
以单内生回归变量的 2SLS 为例，当只有一个内生回归变量 X 和一些其他的包含的外生变量时，感兴趣的方程为：
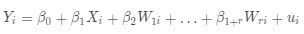（b），
其中同前
可能与误差项相关，但
与误差项不相关。
2SLS 的总体第一阶段回归将 X 与外生变量 W 和工具变量（ Z ）联系在了一起：
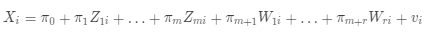(c)
其中
为未知回归系数，
为误差项。
在 2SLS 的第一阶段中，可用 OLS 估计（ c ）式中的未知系数，并记由该回归得到的预测值为
。
在 2SLS 的第二阶段中，用 OLS 估计
用第一阶段的预测值替换后的（ b ）式。也就是用 OLS 估计
关于
，
的回归。得到的
估计量就是 2SLS 估计量。
当存在多个内生回归变量
时，除了每个内生回归变量都需要自己的第一阶段回归以外， 2SLS 的算法是类似的。其中每个内生回归变量的第一阶段回归形式同（ c ）式，即因变量是某个 X ，回归变量是所有工具变量（ Z ）和所有包含的外生变量（W）。所有这些第一阶段回归一起得到了每个内生回归变量的预测值。
在 2SLS 的第二阶段中，用 OLS 估计内生回归变量（X）分别用其预测值（
）替换后的（a）式。得到的
估计量即为2SLS估计量。
3.4 过度识别检验
上面提到了，只有恰好识别和过度识别才能用 IV 方法估计。假设待估参数的个数为 k ，矩条件的个数为 l 。当 k=l 时，称为“恰好识别”，当 k
一个很重要的命题是：
只有过度识别情况下才能检验工具变量的外生性，而恰好识别情况下无法检验。
具体思路如下：工具变量的外生性意味着它们和
不相关。这表明工具变量和
近似不相关，其中
为基于所有工具变量的 2SLS 回归估计残差（由于抽样变异性因此是近似的而不是精确地，注意到这些残差是利用 X 值而不是用其第一阶段的预测值得到的。）
于是，如果工具变量事实上是外生的，那么
关于工具变量和包含的外生变量回归中工具变量的系数都应该等于零，而这个假设是可以检验的。
过度识别约束检验（ J 统计量），又称为 Sargan 统计量。令
为来自（a）式 2SLS 估计的残差。
利用 OLS 估计下面的回归系数：
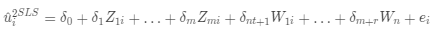(d)
其中
为回归误差项。令 F 表示检验假设
的同方差适用 F 统计量。则过度识别约束检验统计量为 J=mF 。如果
是同方差的，则在所有工具变量都是外生的原假设下， J 服从
分布，其中 m-k 为“过度识别度”，也就是工具变量的个数减去内生回归变量的个数。
3.5 Euler 方程范例
在 Hansen、Singleton （1982）的经典文章中，他们基于消费的资产资本定价模型分析了资产随时间的移动。
在他们的非线性理性预期模型的一个稍微简单的版本中，代表性最大化的期望贴现寿命效用为:
，
其中受到的预算约束为：
,
。其中，
为 t 时刻的阶段性消费；
,
,
是相应到期的价格、数量和资产收益；
是实际工资并且
是时刻t的代理信息集。
Hansen 和 Singleton 使用一个恒定的相对风险厌恶效用函数
，因此优化问题的一阶条件是
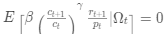,这个看起来像一个母体矩条件但是目前的问题是我们有两个参数
, 只有一个矩条件。
但是，对任意向量
，通过一个迭代的条件期望参数 Euler方程变成：
。
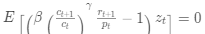因此，从理论上讲，该模型是通过时刻t已知的任何代理变量来识别的，比如
或者
，并且能够利用 GMM 方法一致的估计。与此相反，该模型的极大似然估计需要精确地指定变量的条件分布和大量的数值积分，这些都是计算上的负担。
4. GMM 过程的 Stata 简单实现
4.1 gmm 命令
在 Stata 中， gmm 的一般命令形式为：
gmm ([reqname1:]rexp_1) ([reqname2:]rexp_2) . . . [if] [in] [weight] [,options]
其中：
GMM 的矩估计命令形式为：
gmm moment_pro [if] [in] [weight],
{equations(namelist) | nequations(#)}
{parameters(namelist) | nparameters(#)} [options]
[program_options]
其中，
moment_prog
是以矩条件为基础构造的矩估计表达式。
各个选项具体说明如下：
Model 选项
-
derivative([reqname|#]/name=dexp_jk)
：指定
reqname （或 # ）
对参数名的导数；可指定多于一次。
-
twostep
：使用两步 GMM 估计
-
onestep
：使用一步 GMM 估计
-
igmm
：使用迭代 GMM 估计
-
variables ( varlist )
：在模型中指定变量
-
nocommonesample
：不要限制所有方程的估计样本都是相同的
Instruments 选项
-
instruments([reqlist:]varlist)[,noconstant])
：是制定工具；可以被多次指定
-
xtinstruments([reqlist:]varlist,lags(#_1/#_2))
：是制定面板类工具变量；可以被多次指定
Weight matrix 选项
-
wmatrix(wmtype[,independent])
：指定权重矩阵;
wmtype
可以是
robust
,
cluster
clustvar
,
hac kernel [lags]
，或者
unadjusted
-
center
：计算权重矩阵时的中心矩
-
winitial(iwtype[, independent])
：指定初始权重矩阵；
iwtype
可以是
unadjested
,
identity
,
xt xtspec
,或者 Stata 矩阵的名字
SE/Robust 选项
-
vce(vcetype[,independent])
：其中
vcetype
可以是
robust
,
cluster
clustvar
,
bootstrap
,
jackknife
,
hac kernel lags
,或者
unadjusted
-
quickderivatives
：采用VCE数值导数的另一种计算方法
Reporting 选项
-
level(#)
：设置置信水平;默认是水平( 95 )
-
title(string)
：将字符串显示为参数估计表上方的标题
-
title2(string)
：显示字符串作为副标题
-
display_options
：控制列与列格式、行间距、行宽、显示省略的变量、基单元格与空单元格，以及因子-变量标记
Optimization 选项
-
from(initial_values)
：参数的指定初始值
-
igmmiterate(#)
：指定迭代 GMM 估计的最大迭代次数
-
igmmeps
：迭代的 GMM 参数收敛准则指定为 # ；默认为 igmmeps(1e-6)
-
igmmweps( # )
：迭代的 GMM 权重矩阵收敛准则指定为 # ;默认是 igmmweps (1e-6)
-
optimization_options
：控制优化过程；很少使用
-
coeflegend
：显示图例而不是统计数据
4.2 简单例子
在对 gmm 命令的一般形式有了解之后，此处举个简单的案例来进行 gmm 的分析。以 Stata 自带的数据 auto.dta 为例，进行以下的 GMM 实验：
4.2.1 简单线性回归
Stata 操作为：
sysuse auto,clear
regress mpg gear_ratio turn
gmm (mpg - {b1}*gear_ratio - {b2}*turn - {b0}),instruments(gear_ratio turn
)
结果如下：
. gmm (mpg - {b1}*gear_ratio - {b2}*turn - {b0}),instruments(gear_ratio turn)
Step 1
Iteration 0: GMM criterion Q(b) = 471.67875
Iteration 1: GMM criterion Q(b) = 3.058e-21
Iteration 2: GMM criterion Q(b) = 2.545e-31
Step 2
Iteration 0: GMM criterion Q(b) = 1.691e-32
Iteration 1: GMM criterion Q(b)
= 1.691e-32 (backed up)
note: model is exactly identified
GMM estimation
Number of parameters = 3
Number of moments = 3
Initial weight matrix: Unadjusted Number of obs = 74
GMM weight matrix: Robust
------------------------------------------------------------------------------
| Robust
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
/b1 | 3.033 1.502 2.02 0.043 0.090 5.976
/b2 | -0.733 0.118 -6.21 0.000 -0.964 -0.502
/b0 | 41.218 8.397 4.91 0.000 24.761 57.675
------------------------------------------------------------------------------
Instruments for equation 1: gear_ratio turn _cons
4.2.2 利用线性组合的简单线性回归
Stata 操作为：
gmm (mpg - {xb:gear_ratio turn} - {b0}), instruments(gear_ratio turn)
结果如下：
Step 1
Iteration 0: GMM criterion Q(b) = 471.67875
Iteration 1: GMM criterion Q(b)
= 3.058e-21
Iteration 2: GMM criterion Q(b) = 4.073e-31
Step 2
Iteration 0: GMM criterion Q(b) = 3.566e-32
Iteration 1: GMM criterion Q(b) = 3.566e-32 (backed up)
note: model is exactly identified
GMM estimation
Number of parameters = 3
Number of moments = 3
Initial weight matrix: Unadjusted Number of obs = 74
GMM weight matrix: Robust
------------------------------------------------------------------------------
| Robust
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gear_ratio | 3.032884 1.501664 2.02 0.043 .0896757 5.976092
turn | -.7330502 .117972 -6.21 0.000 -.9642711 -.5018293
-------------+----------------------------------------------------------------
/b0 | 41.21801 8.396739 4.91 0.000 24.76071 57.67532
------------------------------------------------------------------------------
Instruments for equation 1: gear_ratio turn _cons
4.2.3 两阶段最小二乘(与
ivregress 2sls
相同)
最小二乘法的 Stata 操作为：
ivregress
2sls mpg gear_ratio (turn = weight length headroom)
结果为：
Instrumental variables (2SLS) regression Number of obs = 74
Wald chi2(2) = 90.94
Prob > chi2 = 0.0000
R-squared = 0.4656
Root MSE = 4.2007
------------------------------------------------------------------------------
mpg | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
turn | -1.246426 .2012157
-6.19 0.000 -1.640801 -.8520502
gear_ratio | -.3146499 1.697806 -0.19 0.853 -3.642288 3.012988
_cons | 71.66502 12.3775 5.79 0.000 47.40556 95.92447
------------------------------------------------------------------------------
Instrumented: turn
Instruments: gear_ratio weight length headroom
相应 GMM 的 Stata 操作为：
gmm (mpg - {b1}*turn - {b2}*gear_ratio - {b0}), instruments(gear_ratio weight length headroom) onestep
结果如下：
Step 1
Iteration 0: GMM criterion Q(b) = 475.42283
Iteration 1: GMM criterion Q(b) = .16100633
Iteration 2: GMM criterion Q(b) = .16100633
GMM estimation
Number of parameters = 3
Number of moments = 5
Initial weight matrix: Unadjusted Number of obs = 74
------------------------------------------------------------------------------
| Robust
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
/b1 |
-1.246426 .1970566 -6.33 0.000 -1.632649 -.8602019
/b2 | -.3146499 1.863079 -0.17 0.866 -3.966217 3.336917
/b0 | 71.66502 12.68722 5.65 0.000 46.79853 96.53151
------------------------------------------------------------------------------
Instruments for equation 1: gear_ratio weight length headroom _cons
4.2.4 两步 GMM 估计 (与
ivregress GMM
相同)
我们可以使用以下两种语句进行两步 GMM 估计：
ivregress gmm mpg gear_ratio (turn = weight length headroom)
gmm (mpg - {b1}*turn - {b2}*gear_ratio - {b0}), ///
instruments(gear_ratio weight length headroom
) wmatrix(robust)
第一条语句的结果为：
Instrumental variables (GMM) regression Number of obs = 74
Wald chi2(2) = 97.83
Prob > chi2 = 0.0000
R-squared = 0.4769
GMM weight matrix: Robust Root MSE = 4.1559
------------------------------------------------------------------------------
| Robust
mpg | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
turn |
-1.208549 .1882903 -6.42 0.000 -1.577591 -.8395071
gear_ratio | .130328 1.75499 0.07 0.941 -3.30939 3.570046
_cons | 68.89218 12.05955 5.71 0.000 45.25589 92.52847
------------------------------------------------------------------------------
Instrumented: turn
Instruments: gear_ratio weight length headroom
第二条语句的结果为：
Step 1
Iteration 0: GMM criterion Q(b) = 475.42283
Iteration 1: GMM criterion Q(b) = .16100633
Iteration 2: GMM criterion Q(
b) = .16100633
Step 2
Iteration 0: GMM criterion Q(b) = .00863899
Iteration 1: GMM criterion Q(b) = .00741189
Iteration 2: GMM criterion Q(b) = .00741189
GMM estimation
Number of parameters = 3
Number of moments = 5
Initial weight matrix: Unadjusted Number of obs = 74
GMM weight matrix: Robust
------------------------------------------------------------------------------
| Robust
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
/b1 | -1.208549 .1882903 -6.42 0.000 -1.577591 -.8395071
/b2 | .130328 1.75499 0.07 0.941 -3.30939 3.570046
/b0 | 68.89218 12.05955 5.71 0.000 45.25589 92.52847
------------------------------------------------------------------------------
Instruments for equation 1: gear_ratio weight length headroom _cons
4.3 进阶例子
当然 GMM 更有名的应用是在动态面板的估计上，我们可以使用 xtabond 估计动态面板。以 Stata 自带的数据 abdate.dta 为例，进行实验：
webuse abdata,clear
`
`xtabond n L(0/1).w L(0/1).k, lags(1) noconstant vce(robust)
结果如下：
Arellano-Bond dynamic panel-data estimation Number of obs = 751
Group variable: id Number of groups = 140
Time variable: year
Obs per group:
min = 5
avg = 5.364286
max = 7
Number of instruments = 32 Wald chi2(5) = 658.83
Prob
> chi2 = 0.0000
One-step results
(Std. Err. adjusted for clustering on id)
------------------------------------------------------------------------------
| Robust
n | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
n |
L1. | .8041712 .1199819 6.70 0.000 .5690111 1.039331
|
w |
--. | -.5600476 .1619472 -3.46 0.001 -.8774583 -.242637
L1. | .3946699 .1092229 3.61 0.000 .1805969 .6087429
|
k |
--. | .3520286 .0536546 6.56 0.000 .2468676
