今天,九章算法为大家悉心准备了
史上最强的位运算知识点大总结
!

位运算专题
将A的二进制表示的每一位向左移B位,左边超出的位截掉,右边不足的位补0
A = 1100 B = 2
A << B = 110000
右移操作分为算数右移和逻辑右移
算术右移是带符号的右移,逻辑右移是不带符号的右移。
算术右移:将A的二进制表示的每一位向右移B位,右边超出的位截掉,左边不足的位补符号位的数。
逻辑右移:将A的二进制表示的每一位向右移B位,右边超出的位截掉,左边不足的位补0。
C语言:只有逻辑右移 A >> B
JAVA 和 Python中:算术右移 A >> B , 逻辑右移 A >>> B
A = 11111111111111111111111110000001
B = 2
A >> B = 11111111111111111111111111100000
A >>> B = 00111111111111111111111111100000
将A和B的二进制表示的每一位进行与操作,只有两个对应的二进制位都为1时,结果位才为1,否则为0.
A = 001010
B = 101100
A & B = 001000
将A和B的二进制表示的每一位进行或操作,只要两个对应的二进制位有一个为1,结果位就为1,否则为0.
A = 001010
B = 101100
A | B = 101110
将A的二进制表示每一位进行取反操作,如果对应的二进制位为0,结果位为1,否则为0.
A = 00000000000000000000000000001010
~A = 11111111111111111111111111110101
将A和B的二进制表示的每一位进行异或操作,如果对应的二进制位不同,结果位为1,否则为0.
A = 001010
B = 101100
A ^ B = 100110
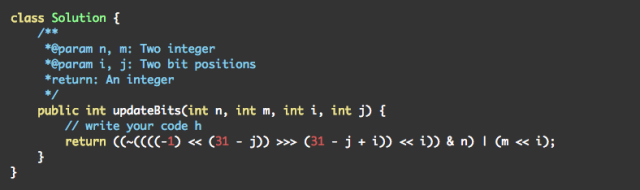
给出两个32位的整数N和M,以及两个二进制位的位置i和j。写一个方法来使得N中的第i到j位等于M(M会是N中从第i为开始到第j位的子串)。
http://www.lintcode.com/zh-cn/problem/update-bits/
思路解析:
根据题意,可以有一个想法,将n中第i位到第j位的先置为0,然后,按位或m << i即可。
现在问题是如何将n中第i位到第j位置为0,可以考虑构造一个数,这个数从第i位到第j位是0,其他位都为1。
这样的数并不是很好构造,所以,我们构造一个数从第i位到第j位都是1,其他位为0的数,然后将这个数取反,就可以得到从第i位到第j位是0,其他位是1的数。
-1的二进制表示是所有位为1,我们以这个数为起点。需要的做的是将高(31-j)位置0,将低i位置0。
将-1先左移(31-j)位,因为高(31-j)位都是不需要的。
然后再将((-1) << (31 - j))逻辑右移(31 - j + i)位,因为要将低i位置0.
然后再将(((-1) <>> (31 - j + i))左移i位,将1恢复到正确的位置即可。即得到第i位到第j位是1,其他位是0的数。
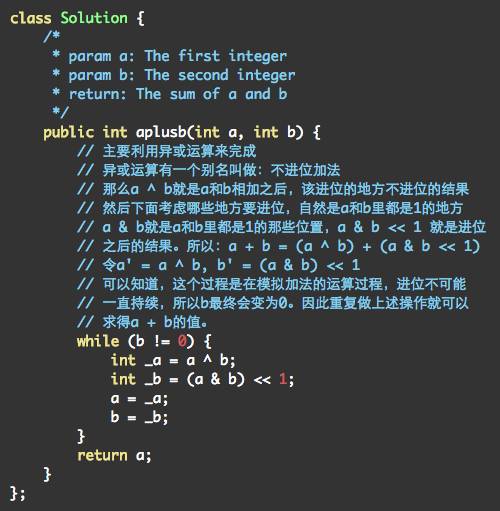
给出两个整数a和b, 求他们的和, 但不能使用
+
等数学运算符。
http://www.lintcode.com/zh-cn/problem/a-b-problem/
思路解析:
这里引用九章答案的答案
http://www.jiuzhang.com/solutions/a-b-problem/
x & (x - 1) 用于消去x最后一位的1
x = 1100
x - 1 = 1011
x & (x - 1) = 1000
用 O(1) 时间检测整数 n 是否是 2 的幂次。
http://www.lintcode.com/zh-cn/problem/o1-check-power-of-2/
思路解析:
N如果是2的幂次,则N满足两个条件。
1.N >0
2.N的二进制表示中只有一个1
因为N的二进制表示中只有一个1,所以使用N & (N - 1)将N唯一的一个1消去,应该返回0。

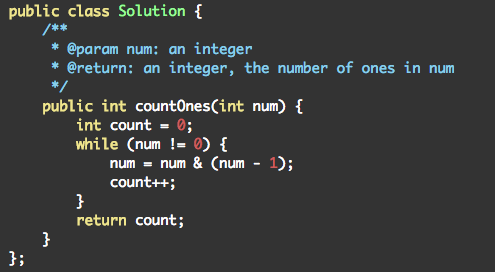
计算在一个 32 位的整数的二进制表式中有多少个 1。
http://www.lintcode.com/zh-cn/problem/count-1-in-binary/
思路解析:
由x & (x - 1)消去x最后一位的1可知。不断使用 x & (x - 1) 消去x最后一位的1,计算总共消去了多少次即可。
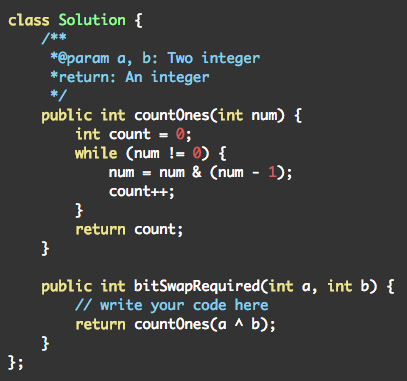
http://www.lintcode.com/zh-cn/problem/flip-bits/
解题思路:
这个应用是上面一个应用的拓展。
思考将整数A转换为B,如果A和B在第i(0<=i<32)个位上相等,则不需要改变这个BIT位,如果在第i位上不相等,则需要改变这个BIT位。所以问题转化为了A和B有多少个BIT位不相同。联想到位运算有一个异或操作,相同为0,相异为1,所以问题转变成了计算A异或B之后这个数中1的个数。
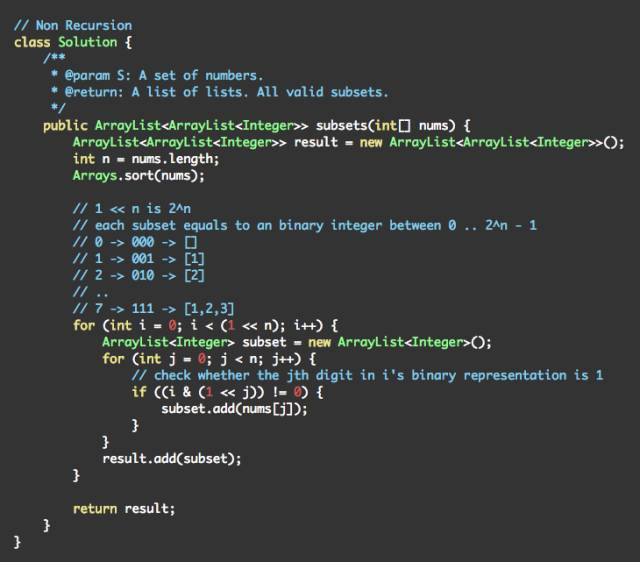
http://www.lintcode.com/zh-cn/problem/subsets/
解题思路:
思路就是使用一个正整数二进制表示的第i位是1还是0,代表集合的第i个数取或者不取。
所以从0到2^n-1总共2^n个整数,正好对应集合的2^n个子集。
S = {1,2,3}
N bit Combination
0 000 {}
1 001 {1}
2 010 {2}
3 011 {1,2}
4 100 {3}
5 101 {1,3}
6 110 {2,3}
7 111 {1,2,3}
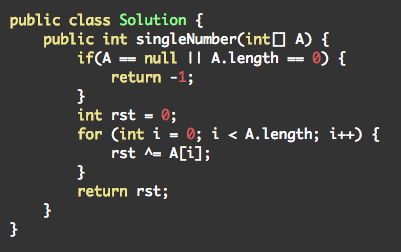
数组中,只有一个数出现一次,剩下都出现两次,找出出现一次的数
http://www.lintcode.com/en/problem/single-number/
思路解析:
因为只有一个数恰好出现一个,剩下的都出现过两次,所以只要将所有的数异或起来,就可以得到唯一的那个数。
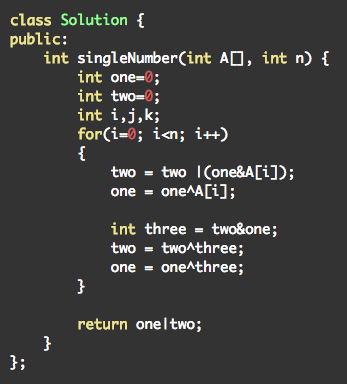
数组中,只有一个数出现一次,剩下都出现三次,找出出现一次的数
http://www.lintcode.com/en/problem/single-number-iii/
解题思路:
因为数是出现三次的,也就是说,对于每一个二进制位,如果只出现一次的数在该二进制位为1,那么这个二进制位在全部数字中出现次数无法被3整除。
膜3运算只有三种状态:00,01,10,因此我们可以使用两个位来表示当前位%3,对于每一位,我们让Two,One表示当前位的状态,B表示输入数字的对应位,Two+和One+表示输出状态。
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 1 0
1 0 1 0 0
One+ = (One ^ B) & (~Two)
Two+ = (~One+) & (Two ^ B)
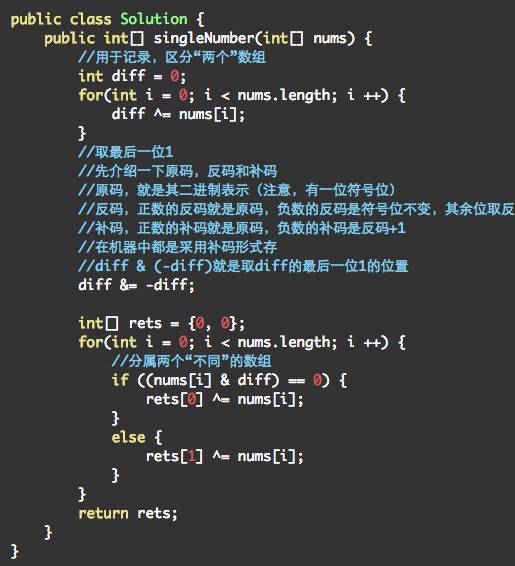
数组中,只有两个数出现一次,剩下都出现两次,找出出现一次的数
http://www.lintcode.com/en/problem/single-number-iii/
思路解析:
有了第一题的基本的思路,我们可以将数组分成两个部分,每个部分里只有一个元素出现一次,其余元素都出现两次。那么使用这种方法就可以找出这两个元素了。
不妨假设出现一个的两个元素是x,y,那么最终所有的元素异或的结果就是res = x^y。并且res!=0,那么我们可以找出res二进制表示中的某一位是1。对于原来的数组,我们可以根据这个位置是不是1就可以将数组分成两个部分。x,y在不同的两个子数组中。而且对于其他成对出现的元素,要么在x所在的那个数组,要么在y所在的那个数组。
《算法强化班》
2017年定制版
课程全面革新
正在报名中!
报名登陆官网
www.jiuzhang.com
或点击文末“阅读原文”






