磁性斯格明子：拓扑磁性的展现

在数学发展的历史长河中，有一个古老的问题：“七桥问题”。原普鲁士的著名城市柯尼斯堡(今俄罗斯加里宁格勒)的市区被河流分成了4 部分，有7 座桥将这4 部分连接起来(如图1 所示，绿色的桥依然存在，红色的桥已经不存在)。关于这座城市，有一个问题长期得不到解决：如果每座桥必须且只能经过一次，通过桥面时不能折返(必须完整地走过每一座桥)，起点和终点不必要重合，在上述条件下，是否有办法通过这7 座桥走完这座城市？1736 年，欧拉(Leonhard Euler)对这一问题作出了否定的回答，即不可能在上述条件下完成这一行走。在回答这一问题时，欧拉创造性地提出了拓扑(topology)的方法，将柯尼斯堡市区抽象成为由7 条线段连接的4 个点。经过每一个点时，如果只能利用某一条线段一次，那么经过一个点的线段数必须是偶数，作为起点或终点，可以有奇数条线段经过，因此整个系统最多只能有两个点的连接数为奇数(或者零个点)。而柯尼斯堡市区的4 片区域之间，每个抽象点的连接数都是奇数，所以不可能在限定条件下完成这一行走。在解决这一问题时，欧拉认为：被研究对象的数学特性与对象的形状没有关联，只与研究对象的拓扑有关。在研究过程中，可以在不改变对象拓扑结构的情况下任意变化研究对象的形状。欧拉所提出的这一数学方法是拓扑研究方法的首次实际应用，成为各个研究领域的拓扑学发展的起点，对科学的发展有非常重要的贡献。

图1 原普鲁士城市柯尼斯堡(今俄罗斯加里宁格勒)的市区地图和欧拉对其作出的拓扑抽象

拓扑学的研究，最早繁荣于数学领域，其中一个奠基性的工作是19 世纪由高斯提出的Linking number，用来描述三维空间中两个闭合曲线之间的winding。这一概念的提出为结理论(knot theory)和其他拓扑学的发展打下了基础。而拓扑(topology)这一词汇的出现则相对较晚，是由Johann Benedict Listing 在1847 年提出的。在数学家开始拓扑学研究的同时，物理学家也开始关注到这一概念，并将其运用到物理研究中，其中早期的开拓者是苏格兰物理学家Peter Tait，他和开尔文(William Thomson)一起推动了早期的拓扑物理学的发展(图2)。在19 世纪60 年代，开尔文首先提出原子与以太中的结(knot)之间的关联。根据这一基本思想，Peter Tait 和开尔文一起发展了结周期表(knot tables)，并且由Peter Tait 在1885 年首次发表了关于10 次交叉的结周期表。随着原子物理和量子力学的发展，原子的奥秘被逐渐揭示，在原子物理学的发展过程中，Peter Tait 和开尔文的结理论被证明并不成功。然而他们的开创性工作为结理论和拓扑物理学的发展奠定了基础，对现代物理学的发展起到了重要作用。

图2 开尔文(William Thomson)和Peter Tait 共同发展了结理论(Knot theory)

最近三十多年来，随着凝聚态物理和量子场论的发展，拓扑理论发挥着越来越重要的作用，在量子霍尔效应和分数量子霍尔效应的理论解释中，拓扑理论发挥了不可取代的作用。同时，在其他的研究领域中，各种各样的拓扑效应被一一发现。1962 年，Tony Skyrme 提出一种受拓扑保护的“粒子”，可以用来解释核物理中的强子(hadrons)，人们将这种具有粒子性质的激发态命名为Skyrmion(斯格明子)。1975 年，Polyakov 在理论上提出一种二维Heisenberg 自旋系统中的亚稳态，其自旋结构与Skyrme 提出的斯格明子一致(图3)，因此人们把这种二维自旋结构称作磁性斯格明子，这也是首次在磁性系统中提出斯格明子这一概念。随后，理论物理学家提出，在二维电子气的量子霍尔态中也存在斯格明子。虽然有一些理论预言，但是磁性斯格明子一直没有被观测到，直到2006 年，作为基态可以稳定存在的磁性斯格明子在理论上终于被提出。根据理论计算，磁性斯格明子可以广泛存在于薄膜材料和体材料中，只需由空间对称性破缺引入手性相互作用(chiral interaction)。由此产生的磁性斯格明子具有理想的二维拓扑自旋结构(图3)：中心自旋向下，周围的自旋逐渐改变方向指向外围，经由面内指向，最终在边界处自旋指向向上，形成一个完整的磁性斯格明子。磁性斯格明子的二维自旋结构可以连续地对应投影到一个球面上，球面上所有的自旋都指向球面外，类比于电荷的概念，此时可以认为球面内存在一个“等效”的磁单极(magnetic monopole)。因此磁性斯格明子可以被视为受拓扑保护的“磁性粒子”，具有许多准粒子的特性。例如，磁性斯格明子可以对流过自己拓扑自旋结构的电子产生一个等效的磁场，单个磁性斯格明子产生的等效磁场为一个flux quantum( Φ₀ = hc/|e| )，等效磁场方向指向上(垂直于二维平面)。

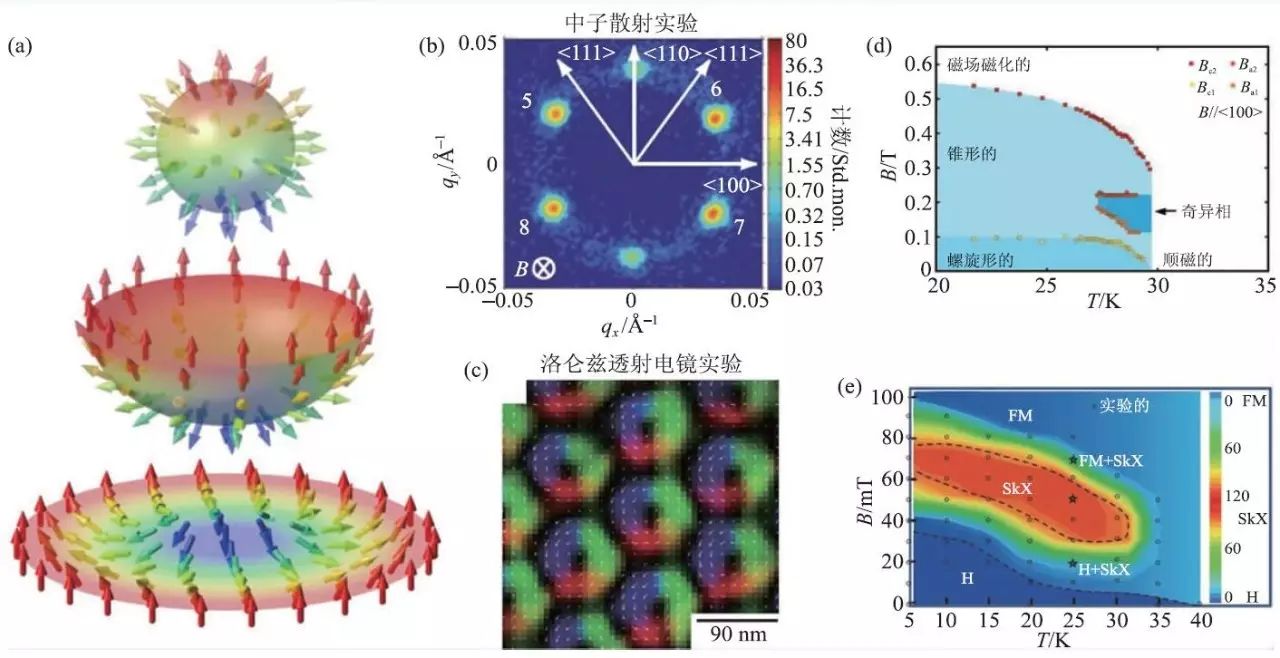
图3 (a)理想的斯格明子自旋结构示意图，磁性斯格明子的自旋方向可以由二维平面向球面进行对应的映射；(b)Mühlbauer 等人利用中子散射实验测量的斯格明子的衍射点；(c)Yu 等人利用洛仑兹透射电镜得到的磁性斯格明子在实空间的自旋分布；(d)中子散射实验得到的温度与磁场相图；(e)洛仑兹透射电镜得到的温度与磁场相图

2009 年，Mühlbauer 等人在实验中利用中子散射测量了MnSi 单晶体材料样品，并且成功观测到磁性斯格明子在倒空间中形成的中子衍射点，这个实验首次证实了磁性斯格明子的存在，为研究拓扑磁性铺平了道路。随后，Yu 等人利用洛仑兹透射电镜对Fe_0.5Co_0.5Si 单晶样品中的磁性斯格明子进行了实空间磁成像，首次清晰地展示了磁性斯格明子的拓扑自旋结构，并确认了手性涡旋自旋结构的长程有序性。Heinze 等人利用自旋极化扫描电子显微镜对Ir(111)衬底上的单层Fe 膜进行测量，也实现了对磁性斯格明子自旋结构的实空间成像。2014 年，Park 等人利用基于透射电镜的电子全息成像技术，对磁性斯格明子的拓扑自旋结构进行了三维全息成像，第一次完整地呈现出磁性斯格明子在三维实空间中的拓扑自旋结构。至此，磁性斯格明子的存在已经得到了充分的实验证据，这些探索性的实验研究工作为研究拓扑磁学创造了有利的条件，使得拓扑磁学的研究进入了一个崭新的阶段。

在磁性体材料中，如果空间对称性破缺引入手性相互作用，例如Dzyaloshinskii—Moriya Interaction(DMI)，在只考虑最近邻交换相互作用和外磁场导致的Zeeman 能的情况下，磁性系统的总能量可以表述为

其中E_ex = -JM_i∙M_j 是最近邻交换相互作用能，E_DM = -D_ijM_i ×M_j 是DMI 导致的手性相互作用能， E_zeeman = -B∙M_i 是外磁场导致的Zeeman 能。根据E_ex 和E_DM 的相对大小，可以在一定外磁场和温度范围内，形成磁性斯格明子的基态或亚稳态。根据不同的DMI的方向，可以形成布洛赫型(Bloch type)的磁性斯格明子或奈尔型(Néel type)的磁性斯格明子(图4)，并且磁性斯格明子的自旋周期长度a_sk 正比于J/D，可以在数纳米到数微米的范围内变化。目前已经发现的大部分体材料磁性斯格明子都属于布洛赫型，其中大部分均属于B20 立方结构的材料，比如MnSi，Mn_1-xFe_xSi，Fe_1-xCo_xSi，MnGe，Mn_1-xFe_xGe，FeGe，Cu₂OSeO₃等等，另外还有β-Mn 型结构的Co₁₀Zn₁₀，这也是唯一一种可以在温度高于室温的情况下稳定的体材料磁性斯格明子。而奈尔型的体材料磁性斯格明子比较稀少，目前仅在GaV₄S₈中观测到。由于DMI相对于最近邻交换相互作用来说普遍较弱，只有在低温下才可能体现出效果，而低温下较弱的热激发又会阻碍磁性斯格明子的产生，因此体材料磁性斯格明子往往只可能存在于温度与磁场相图中的小区域范围中，如图3 所示。另外，体材料磁性斯格明子往往出现在一些复杂的单晶化合物中，对晶体质量要求很高。上述两个限制条件严重阻碍了体材料磁性斯格明子的研究和应用。人们迫切需要寻找一种可以在温度与磁场相图中的大范围区域中稳定的、制备要求较低的、能够和传统磁性器件匹配的磁性斯格明子材料。目前有两种类型的磁性斯格明子材料可以满足上述几个要求，一种是人工斯格明子，另一种是基于界面自旋轨道耦合的磁性多层膜。

在磁性薄膜中，为了降低磁偶极能，磁矩方向一般平行于薄膜表面。因此，利用磁性薄膜的形状效应，在磁性材料微纳尺度的结构中可以形成涡旋磁结构(magnetic vortex)，利用层间耦合可以将这一涡旋磁结构印刷进一个具有垂直磁各向异性的磁性薄膜中，从而形成一个人工斯格明子。早期的微磁学模拟证实了这一猜想，而实验上首个人工斯格明子是在Co/Ni/Cu(001)单晶薄膜中实现的。在单晶的Cu(001)衬底上外延生长Ni 的单晶薄膜，在7 至50 个原子单层的厚度区间，Ni 薄膜具有垂直磁各向异性。通过原位成型的实验手段，在Ni 薄膜表面制备30 nm 厚的Co 圆盘(直径2 μm)。30 nm 厚的Co 圆盘在形成涡旋磁结构时，可以将磁结构印刷入Ni 薄膜中，从而形成一个完整的人工斯格明子(图4)。类似的人工斯格明子在Co/[Co/Pd]n磁性多层膜中也可以实现。相较于体材料磁性斯格明子，人工斯格明子的一大优势就是稳定性，利用磁性3d过渡金属的高居里温度的特点，可以保证人工斯格明子在较大温度范围内保持自旋结构的稳定。具有垂直磁各向异性的磁性薄膜具有较大的矫顽场(至少数百高斯)。而涡旋磁结构在获得拓扑保护后，可以在较大磁场下保持稳定，其磁核心(vortex core)的垂直翻转磁场可达数千高斯。因此人工斯格明子的稳定性要优于体材料磁性斯格明子。然而，人工斯格明子的形成离不开磁性微纳米结构，而磁性微纳米结构反过来限制了人工斯格明子的运动自由度，使得人工斯格明子的应用价值降低。

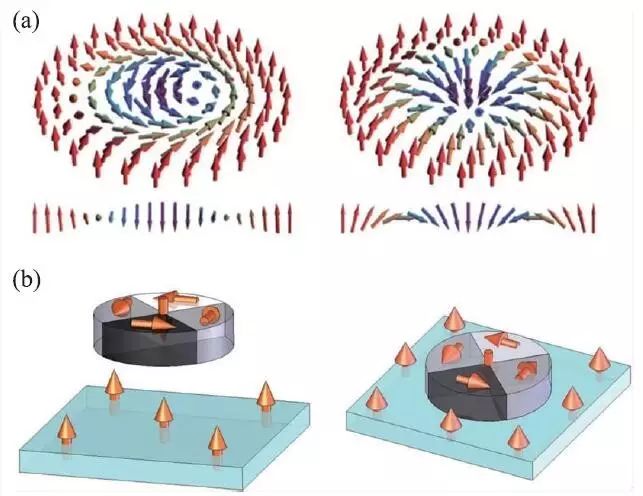
图4 (a)布洛赫型(Bloch type)的斯格明子和奈尔型(Néel type)的斯格明子自旋结构示意图；(b)人工斯格明子的制备示意图

从磁性斯格明子的稳定性、制备容易度、集成化磁性器件的兼容性等因素考量，磁性多层膜成为了实现磁性斯格明子的最优选择。在具有垂直磁各向异性的磁性多层膜中，由于垂直磁各向异性和磁偶极能之间的相互竞争关系，在磁矩从薄膜面外到薄膜面内的自旋重转向相变的过程中，可以形成条状磁畴和磁泡。其中，磁泡中的自旋结构可以分为平庸自旋结构和非平庸拓扑自旋结构，而非平庸的磁泡对应着一个完整的磁性斯格明子(图5)。在磁性薄膜中，如果只考虑最近邻交换相互作用、垂直磁各向异性和磁偶极能，则平庸磁泡和非平庸磁泡将随机出现。为了形成长程有序的磁性斯格明子(非平庸的磁泡)，必须计入手性相互作用(DMI)，即满足空间对称性破缺和有效的自旋轨道耦合，而这一条件可以利用过渡金属与贵金属之间的界面来实现，在具有垂直磁各向异性的磁性双层膜中(例如Co/Pt，Co/Ir 等)，由于界面处的空间对称性破缺，可以导入手性相互作用，同时考虑贵金属所导入的强自旋轨道耦合，就可以在磁泡的自旋结构中，确保非平庸拓扑自旋结构的形成。按照这一思路合成的磁性斯格明子，可以在室温下稳定，并且可以有效地制备成磁性器件，具有广泛的应用价值。目前，磁性多层膜中的斯格明子已经在Ta/CoFeB/TaO，Ir/Co/Pt，Pt/Co/MgO，Pt/CoFeB/MgO等体系中实现，基于磁性斯格明子的磁性器件也有望通过这类磁性多层膜实现。

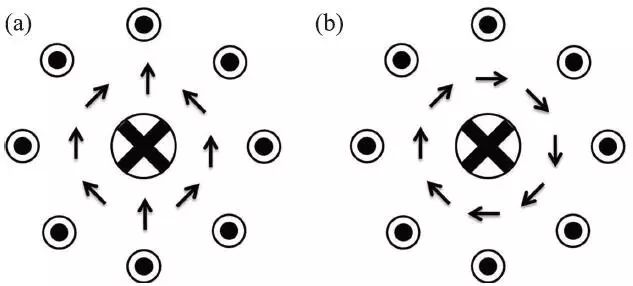
图5 (a)平庸磁泡；(b)非平庸磁泡(即磁性斯格明子)

磁性斯格明子是一种非共线性(non-collinear)的手性自旋结构，带有拓扑性质，其拓扑性质体现在由手性自旋所构成的闭合曲面(即图3 中的球面)，可以用拓扑数N_sk 来表征：

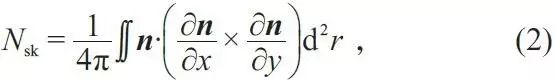
其中n = M/|M| ，当一个电子的自旋在这个闭合曲面上运动时，其波函数会引入一个相位(Berry phase)，可以表述为exp[iA(r)∙Δr] ，其中A(r) 表示矢势。相应的“等效磁场”(Berry curvature)可表示为Ω(r) =∇_r × A(r) ，由此同样可以得到某个自旋结构的拓扑数N_sk = 1/4π ∬Ω(r)d²r 。因此非共线性的手性自旋结构可以在实空间中产生Berry phase，并可以由拓扑数N_sk 来表示。对于磁性斯格明子，拓扑数N_sk 为整数，以图5 中的非平庸磁泡为例，其拓扑数可以为N_sk = ±1 。

由于Berry phase 的存在，电子在这个闭合曲面上运动时， 会感受到emergent magnetic field( Br^e )和emergent electric field( Er^e )，可以表述为

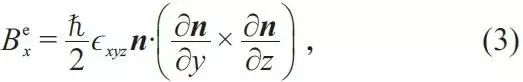
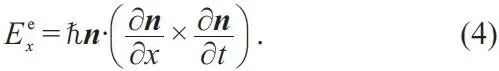
如果有电荷以v_e 的速度流过磁性斯格明子，由于emergent magnetic field ( Br^e )的存在，会产生一个横向电场E^s = v_e × B^e ，此效应可以类比电子在磁场中所受到的洛仑兹力。假设磁性斯格明子在电流驱动下以v_d 的速度移动，根据公式(3)和公式(4)，可以产生一个横向的电场E^e = -v_d × B^e 。最终的横向电场就是这两个电场合成之后的结果，并且总的横向电场正比于B_r^e ，而emergent magnetic field ( B_r^e )是正比于拓扑数N_sk 的，因此可以把这个效应称为拓扑霍尔效应(topological Hall effect)。当磁性斯格明子的尺寸远大于(非自旋翻转)电子散射长度时，拓扑霍尔效应由实空间中的Berry phase 主导；而在磁性斯格明子的尺寸接近或小于(非自旋翻转)电子散射长度时，拓扑霍尔效应由动量空间中的Berry phase主导。

与其他平庸的自旋结构不同，作为一个非平庸的拓扑自旋结构，磁性斯格明子在电流驱动下展现了独特的动力学性质，并且吸引了大量的关注和研究，展现出了潜在的应用价值。其动力学方程可以描述为

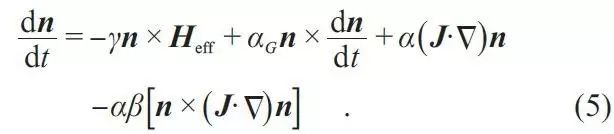
公式(5)右边的第一项为等效外磁场产生的力矩，第二项为Gilbert damping 项，第三项是绝热近似下的自旋转移力矩，而最后一项为非绝热近似下的自旋转移力矩。在平庸的自旋结构中，自旋转移力矩驱动磁畴壁移动，需要较大的电流密度(10⁷ A/cm²)。而作为非平庸的拓扑自旋结构，磁性斯格明子有望降低操控时的电流密度，从而推动电流驱动的磁性器件的改进和发展。在磁性斯格明子被实验证实后，立刻就有实验证据表明，磁性斯格明子的驱动电流远远小于平庸的磁畴壁(10² A/cm²)。这一实验结果也得到了重复验证，证实了磁性斯格明子和电流之间耦合的高效性。相关的理论工作讨论了这一特性的物理原因，认为有两个因素在其中占据了主导作用：(1)磁性斯格明子的拓扑自旋结构；(2)由此拓扑自旋结构引起的Magnus force，而这一Magnus force 正是拓扑霍尔效应的逆效应。另外，理论工作还研究了受限系统中的磁性斯格明子在电流下的自旋动力学性质，从一系列的计算结果可以看出，受限系统中的边界对磁性斯格明子会产生阻尼的效果，因此磁性斯格明子在受限系统中的运动需要更大的驱动电流密度。另外，公式(5)中的非绝热近似下的自旋转移力矩在磁性斯格明子的运动过程中起到了非常重要的驱动作用，简单来说，当非绝热近似的自旋转移力矩增强时，电流驱动的效果也会更加显著。

近期，相关的实验工作更加清晰地展现了磁性斯格明子在电流驱动下的动力学特征。首先，在受限体系中，驱动磁性斯格明子确实需要更大的电流密度(大约是10⁴-10⁷ A/cm²)。其次，在磁性斯格明子沿着电流方向运动的过程中，Magnus force 会引起一个明显的横向偏转，横向偏转的方向取决于磁性斯格明子的自旋拓扑结构。目前，如何在受限系统中降低磁性斯格明子的驱动电流密度，成为了实验研究的一个重点问题。在[Pt/Co/Ta]₁₅多晶磁性多层膜中，驱动电流密度可高达10⁷ A/cm²，界面的杂质缺陷和由此产生的手性相互作用(DMI)的不均匀性，会对磁性斯格明子的运动产生阻碍，当不均匀场的周期与磁性斯格明子的尺寸可比拟时，这一阻碍效果会被放大。为了降低杂质缺陷的影响，需要对样品的组分材料进行优化，例如， 在Ta/CoFeB/TaO 和Pt/CoFeB/MgO中，由于CoFeB 薄膜生长过程中，杂质缺陷被极大抑制，使得驱动电流密度大大减小，可低至10⁴ A/cm²。

作为非平庸的拓扑自旋结构，磁性斯格明子拥有非零的拓扑数，而平庸自旋结构的拓扑数为零，这种拓扑自旋结构上的差别会体现在磁性斯格明子的产生和湮灭过程中。早在磁性斯格明子被实验观测到之前，理论物理学家已经提出：在绝热近似下，磁性斯格明子受拓扑保护，通过连续的自旋转动变化，无法完成磁性斯格明子的产生和湮灭。换而言之，在绝热近似和自旋连续转动近似下，非平庸拓扑自旋结构和平庸拓扑自旋结构无法相互转换，这种拓扑自旋结构上的转换需要引入额外的磁单极(magnetic monopole 和magnetic anti-monopole)，而额外磁单极的引入需要额外的能量。因此，磁性斯格明子的拓扑自旋结构是受到拓扑保护的。

在实验中，这种拓扑保护效应也得到验证。例如，在利用自旋极化扫描隧道显微镜(SP-STM)对磁性薄膜中的斯格明子进行读操作和写操作时，人们发现产生和湮灭磁性斯格明子所需的自旋极化电流存在滞后现象，这一滞后现象已经揭示了磁性斯格明子的拓扑保护效应。而之后在对人工斯格明子的研究中，这种拓扑保护现象则更清晰地被揭示出来。通过实验，人们发现从一个非平庸的磁性斯格明子变化到平庸的磁单畴状态，比两个平庸自旋结构之间的转换需要更大的外磁场，两个过程中临界磁场的差别清晰地体现了磁性斯格明子的拓扑保护现象(图6)。

图6 湮灭平庸磁性斯格明子(N_sk=0)的临界磁场小于110 Oe，湮灭非平庸磁性斯格明子(N_sk=1)的临界磁场小于160 Oe。两者之间的差别直接体现了磁性斯格明子的拓扑保护现象

而这种拓扑保护现象在理论研究中也同样得到体现。在理论计算中，人们发现，从平庸状态转换到非平庸磁性斯格明子的过程中，需要额外的辅助能量(例如，热辅助)。这一结果也体现出了磁性斯格明子的拓扑保护效应。

拓扑和磁学都是古老的研究领域，而拓扑磁性则是近年来兴起的新兴研究方向。作为拓扑磁性的第一个完美研究对象，磁性斯格明子的研究才刚刚开始，磁性与拓扑之间的关联还需要更多的研究工作来揭示，拓扑磁性的奥秘依然等待着进一步的探索。除了对拓扑磁性的基础物理问题的研究兴趣，磁性斯格明子在工业应用中的前景也激励着应用性的研究工作。如何得到更稳定的磁性斯格明子材料？如何降低磁性斯格明子的驱动电流密度？如何将磁性斯格明子与现有的磁性器件进行整合？如何利用磁性斯格明子产生更多的新功能磁性器件？这一系列的疑问将激励研究者的探索热情，从物理兴趣和工业应用两方面推动拓扑磁性这一研究领域的进一步发展。