
来源:
超级数学建模
作者:不会停的蜗牛
导读:
通过本篇文章可以对ML的常用算法有个常识性的认识,没有代码,没有复杂的理论推导,就是图解一下,知道这些算法是什么,它们是怎么应用的,例子主要是分类问题。
每个算法都看了好几个视频,挑出讲的最清晰明了有趣的,便于科普。 以后有时间再对单个算法做深入地解析。
今天的算法如下:
-
决策树
-
随机森林算法
-
逻辑回归
-
SVM
-
朴素贝叶斯
-
K最近邻算法
-
K均值算法
-
Adaboost算法
-
神经网络
-
马尔可夫
1.
决策树
根据一些 feature 进行分类,每个节点提一个问题,通过判断,将数据分为两类,再继续提问。这些问题是根据已有数据学习出来的,再投入新数据的时候,就可以根据这棵树上的问题,将数据划分到合适的叶子上。
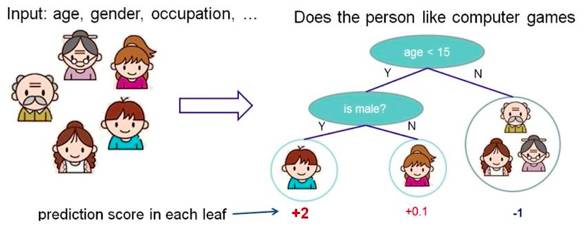
2、随机森林
在源数据中随机选取数据,组成几个子集:
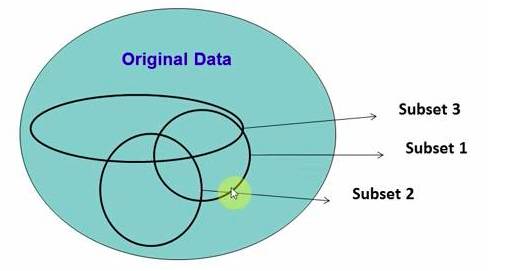
S矩阵是源数据,有1-N条数据,A、B、C 是feature,最后一列C是类别:
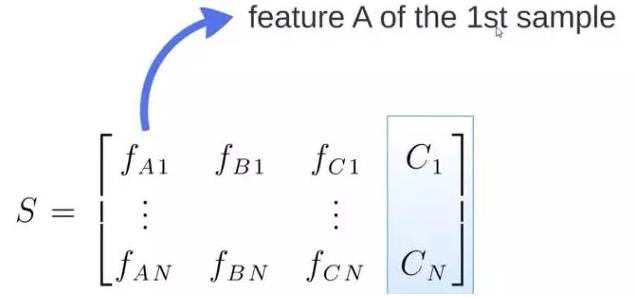
由S随机生成M个子矩阵:

这M个子集得到 M 个决策树:
将新数据投入到这M个树中,得到M个分类结果,计数看预测成哪一类的数目最多,就将此类别作为最后的预测结果。
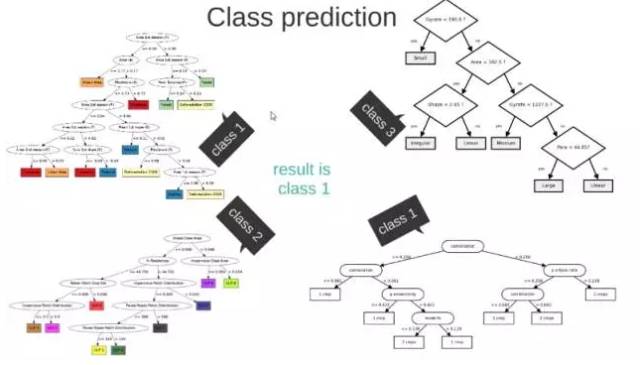
3、逻辑回归
当预测目标是概率这样的,值域需要满足大于等于0,小于等于1的,这个时候单纯的线性模型是做不到的,因为在定义域不在某个范围之内时,值域也超出了规定区间。
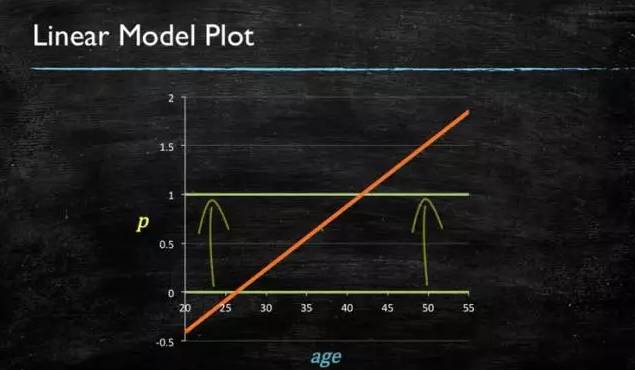
所以此时需要这样的形状的模型会比较好:
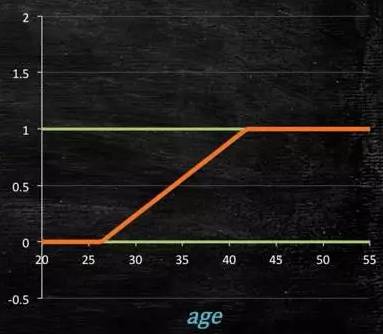
那么怎么得到这样的模型呢?
这个模型需要满足两个条件 “大于等于0”,“小于等于1”
大于等于0 的模型可以选择绝对值,平方值,这里用指数函数,一定大于0;
小于等于1 用除法,分子是自己,分母是自身加上1,那一定是小于1的了。
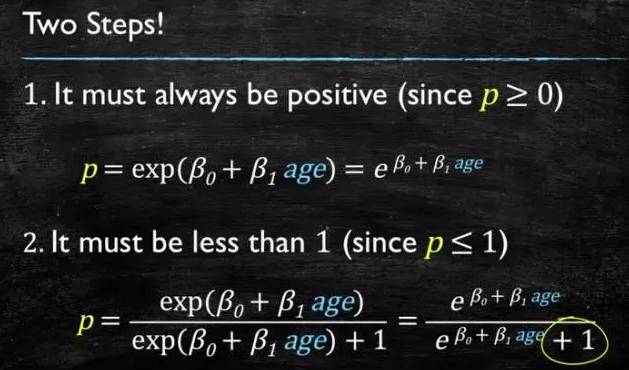
再做一下变形,就得到了 logistic regressions 模型:

通过源数据计算可以得到相应的系数了:

最后得到 logistic 的图形:
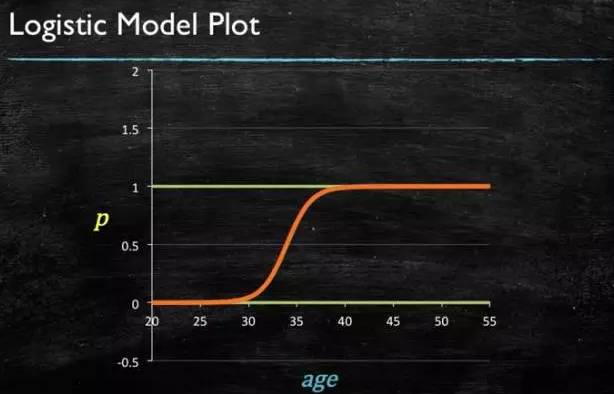
4、SVM
要将两类分开,想要得到一个超平面,最优的超平面是到两类的 margin 达到最大,margin就是超平面与离它最近一点的距离,如下图,Z2>Z1,所以绿色的超平面比较好。
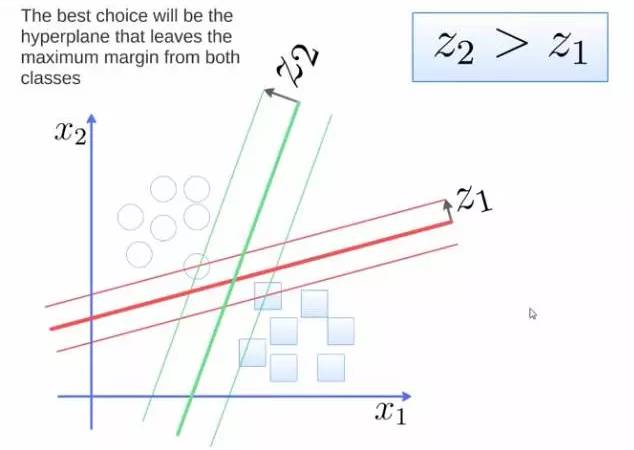
将这个超平面表示成一个线性方程,在线上方的一类,都大于等于1,另一类小于等于-1:
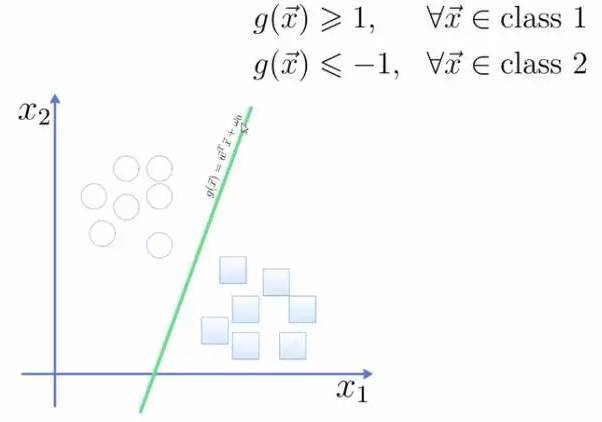
点到面的距离根据图中的公式计算:
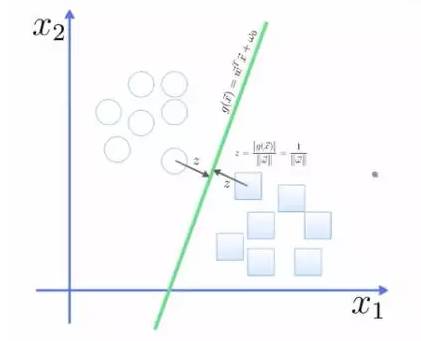
所以得到total margin的表达式如下,目标是最大化这个margin,就需要最小化分母,于是变成了一个优化问题:
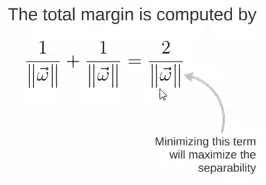
举个例子,三个点,找到最优的超平面,定义了 weight vector=(2,3)-(1,1):
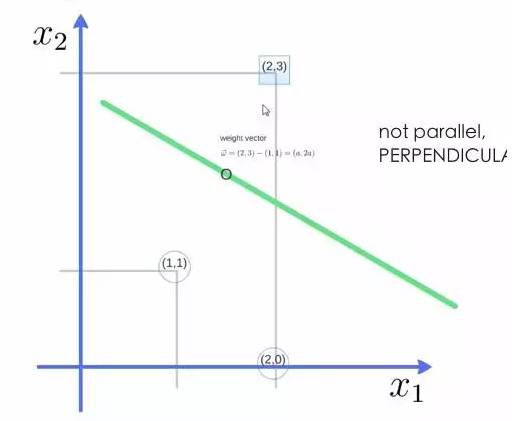
得到weight vector为(a,2a),将两个点代入方程,代入(2,3)另其值=1,代入(1,1)另其值=-1,求解出 a 和 截矩 w0 的值,进而得到超平面的表达式。
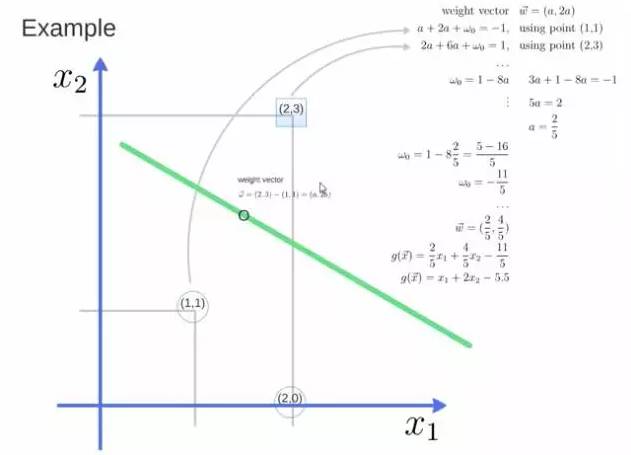
a求出来后,代入(a,2a)得到的就是support vector,
a和w0代入超平面的方程就是support vector machine。
5、朴素贝叶斯
举个在 NLP 的应用:
给一段文字,返回情感分类,这段文字的态度是positive,还是negative:






