本文共
5400字
，
建议阅读
10
分钟。
本文为你介绍一条在计算机辅助几何设计领域、计算力学领域有着根本的重要性的定理。
一条本应该数十年前就被发现的定理，在计算机辅助几何设计领域、计算力学领域有着根本的重要性，最近终于被证明【1】。
2019年六月下旬，国际数字几何峰会在加拿大温哥华召开。温哥华是一座独特而又美丽的城市。这里气候冬暖夏凉，温和湿润，在六月酷暑的骄阳中，老顾感到了刺骨的寒冷。英属哥伦比亚大学（UBC）的天体海滩在一片海湾之中，海滩对岸是蓊郁苍翠的群山，山顶覆盖着皑皑白雪。浩瀚的太平洋给温哥华带来了丰富的水产，这里的螃蟹、牡蛎享誉全球。香港移民而来的厨师，令温哥华的海鲜粤菜闻名天下。温哥华的艺术文化氛围极为浓厚，经常遇到街头的艺术家在涂鸦作画，满墙的涂鸦作品也极具水准。这里酒吧舞厅林立，周末年轻人彻夜狂欢，摇滚乐通宵震耳欲聋。街头的年轻人也多有纹身，佩戴鼻钉耳环，自由不羁。这里的社会氛围极其包容，经常看到年轻人当街围成一圈，分享吸食一根大麻。空气中时刻弥漫着大麻特有的气味。这里的政府每天为瘾君子免费提供食物和注射毒品，因此吸引了全世界的流浪汉。和纽约街头游荡的流浪汉相比，这里的流浪汉更加精神饱满，温和亲切，毫无暴戾之气。经常有流浪汉横卧街头，面带微笑地注视着每一个过往行人，似乎已不拘物外，斟破人生。
在温哥华，老顾见到了一位三十年未曾见面的老同学。老同学的父母都是大学教授，目睹父辈经济窘困的生活，老同学在商界沉浮半生，实现了财富自由，目前移民温哥华，和黄圣依比邻而居。在温哥华老城，“温哥华”先生的铜像附近，老同学宴请老顾海鲜大餐。夕阳西下，海风吹拂，灯影摇曳，大麻微醺（路人抽的）。在温哥华的夜色中，两人回顾半生经历，不禁唏嘘慨叹。我们两人出身自经济文化闭塞落后的边远地区，匮乏的童年令我们对外面的世界充满瑰丽的想像。逝去的人生经历远远超出了最为狂悖的幻想。在海外漂泊数十年，世事沉浮，历尽沧桑。老同学选择了入世经商，追求财富；老顾选择了出世治学，追求学问，价值观念不同，人生经历迥异，在温哥华不期而遇之后，回顾人生，对照印证，令人再度思考生命的意义。几天后，和科技大学的陈发来教授在温哥华的和平饭店吃正宗川菜，席间陈教授无意间说了一句话，对学者的生命意义给出恰切的总结：“作为一个学者，人们记住你，不是因为你的头衔，而是因为你的工作。”
同期召开的计算机视觉大会有上万学者参加，数字几何非常小众，仅有两百人与会。这一领域处于基础数学和计算机科学相交叉的领域，很多学者同时具有数学和计算机科学的双重背景。老顾见到了很多老朋友，王文平，Konrald Polthier，胡事民，Jorg Peters，陈发来，Helmut Pottman等教授。他们都同时既是微分几何学家也是数字几何学家。相近的知识结构使得思想交流非常直截了当，很多时候一句话就会彼此心领神会。例如这次，老顾向他们介绍了近期发现的一个定理就只说了一句话：“我们证明了四边形网格和黎曼面上亚纯四次微分的等价性，从而由阿贝尔定理得到四边形网格奇异点构型的充要条件。“大家都迅速理解了内在含义，并显示了浓厚的兴趣。陈教授鼓励老顾在博客中通俗解释这一理论。
图1. 样条曲面
在机械设计、计算力学、计算机辅助设计等领域，自由曲面都被表示成所谓的样条曲面，即由分片有理多项式曲面光滑拼接而成，全局二阶可导。样条曲面的架设需要将曲面表达成四边形网格。因此，四边形网格生成技术在机械领域具有根本的重要性。众所周知，在计算力学的模拟仿真过程中，人们需要在网格上求解各种物理偏微分方程，往往求解方程只需要一天，但是生成高质量网格却需要一个月。自动生成高质量的四边形网格一直是这一领域的工程师梦寐以求的理想。
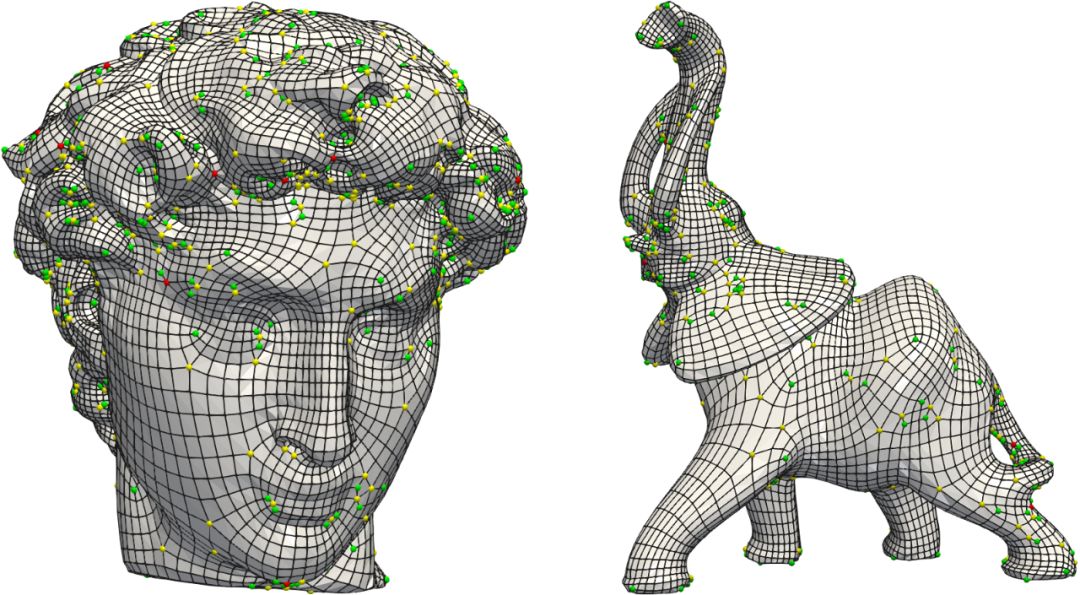
图2. 四边形网格和奇异点（可视化制作，徐考基）
目前通行的四边形网格生成方法如下：首先，人们在曲面上构造光滑的标架场（Frame Field）, 然后构造两族光滑曲线，一族和标架的水平轴相切，另一族和铅直轴相切，两族曲线将曲面进行胞腔分解，每个胞腔都是一个四边形。这一方法的困难在于曲面上不存在处处光滑的标架场，总会有一些奇异点，奇异点处标架的方向不定。在生成的网格中，每个顶点的拓扑度定义为与之相邻的四边形的个数。正常顶点的拓扑度为4，奇异顶点的拓扑度不等于4。如何精确决定奇异点的位置和拓扑度是四边形网格生成的核心困难之一。
四边形网格天然具有不同的几何拓扑结构。比如，四边形网格的组合结构满足欧拉公式，顶点数加上面数减去边数等于曲面的欧拉示性数。四边形网格也具有黎曼度量结构，如果我们将每个四边形的面视为单位正方形，那么我们为四边形网格定义了一个黎曼度量。在这个黎曼度量下，正常点的高斯曲率为零，奇异点的离散高斯曲率等于角欠，
,
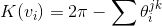根据高斯-博纳定理，总曲率等于
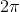乘以欧拉示性数。
那么，是否组合结构的欧拉公式和黎曼度量结构的高斯-博纳定理就完全刻画了四边形网格的奇异点构型呢？换言之，在曲面上用户随意指定有限点集，并且指定每个点的拓扑度，并且满足欧拉公式和高斯-博纳公式，那么是否存在一个四边形网格满足用户指定条件？
答案是否定的，我们考察下面的一个简单得无法再简单的例子：在亏格为1的封闭曲面上，是否存在一个四边形网格，只有一个拓扑度为3的奇异点和一个拓扑度为5的奇异点？
我们发现，如果这样的四边形网格存在，那么其组合结构满足欧拉公式；同时用离散黎奇流方法，可以得到满足高斯-博纳公式的度量。因此，我们无法排除这种四边形网格的存在性。但是无论我们多么努力地尝试，我们却无法真正构造这种四边形网格。这意味着四边形网格具有某种隐含的几何结构还没有被人类充分认识。
这种情形在工程领域经常发生，一项非常基本的技术，人类社会每天都需要用到，计算机可以自动完成99%的任务，但是最后的1%却不得不求助于人类的灵性，才能彻底完成。在所有的机械设计公司，都有一批资深专家，他们终生致力于网格生成，用每个人常年打磨的精湛技艺、画龙点睛般地修葺自动生成的网格，以达到实用要求。这些专家的技艺无法用数学或者工程语言来精确表达，只能世代口耳相传、成为一门神秘的艺术。能否将这种艺术变成一门技术，使得网格生成彻底自动化，从而脱离手工干预，其核心在于奇异点构型的彻底理解。
在过去的数十年间，在世界各地的所有机械设计公司中，从波音、因特尔到丰田，无数的工程师在整个技术生涯中，几乎天天遇到这一问题，但是一直没有本质突破。最近，老顾的团队从迥异的视角深入地思考了这一问题，取得了实质性的突破。
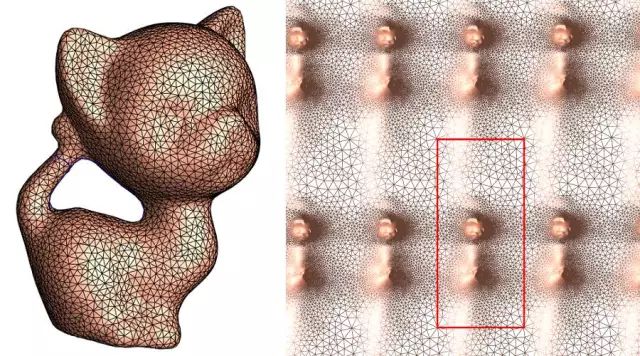
图3. 亏格为1的曲面共形地映射到平面上，每个周期被称为基本域
我们通过解剖一只麻雀来说明这一实质性的突破究竟在哪里。给定一个亏格为1的封闭曲面，根据黎曼-庞加莱单值化定理，我们可以共形地将曲面周期性地平展到平面上，其中的一个周期被称为是一个基本域。
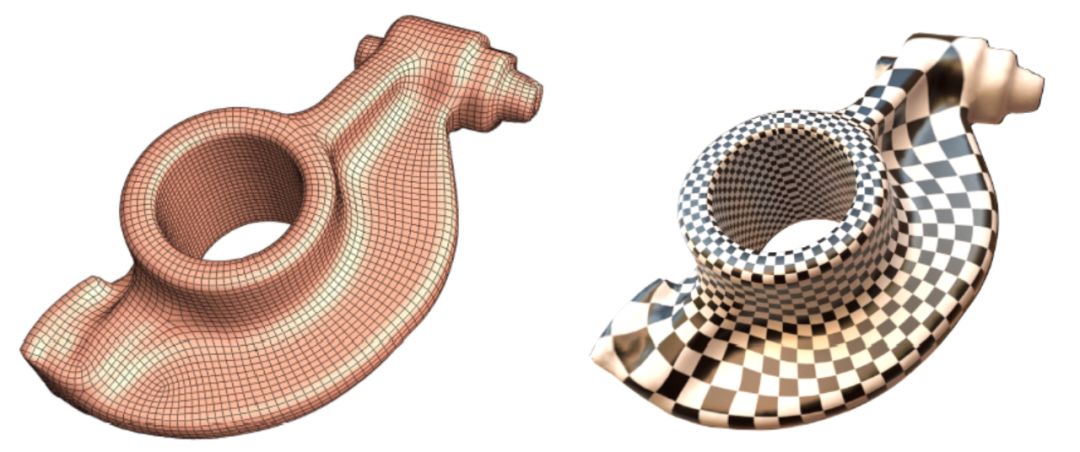
图4. 亏格为1的四边形网格和全纯微分
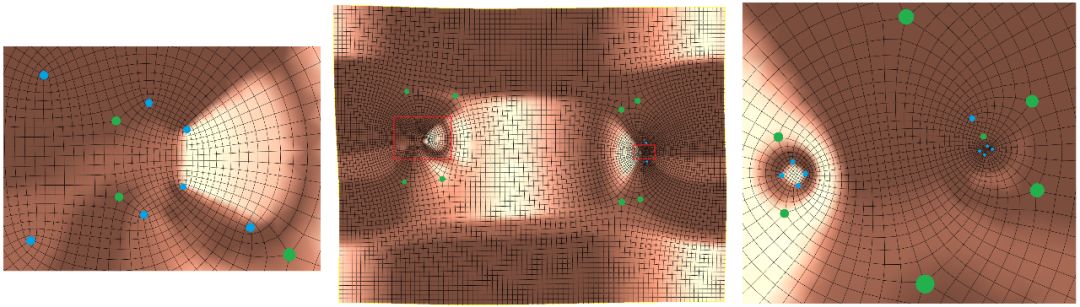
图5. 零极点的Abel-Jacobi映射的像
给定一个亏格为1的封闭四边形网格，我们设每个面是标准正方形，用由此得到的黎曼度量计算单值化共形映射，在其单值化的基本域内，所有极点的重心与所有零点的重心重合。如图5所示，这里有18个零点和18个极点，其坐标总和为零。这种规律对于所有亏格为1的封闭四边形网格都成立，这是迄今为止，前人都没有揭示过的现象。这一发现，及其对于一般拓扑曲面的推广，实质性地推进了四边形网格生成的基础理论发展。
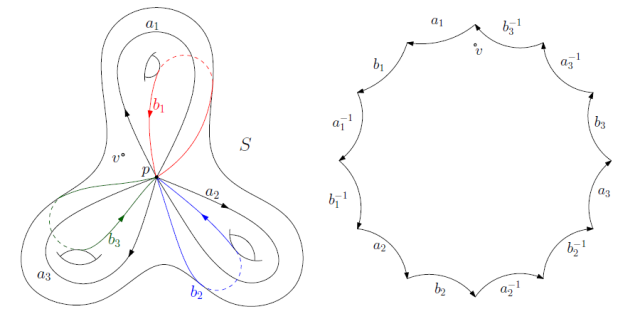
图6. 典范基本群基底和基本域
我们下面用较为严密的数学语言来解释四边形网格奇异点构型的条件。假设M是一个亏格为g的封闭曲面，嵌入在三维欧氏空间之中，因而具有欧氏度量诱导的度量
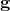。我们选取曲面的典范基本群基底
，
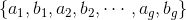满足条件：
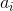和
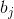的代数相交数为
，
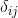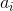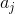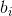和
,
和
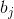的代数相交数都为0。我们将黎曼面沿着基本群典范基底切开，得到一个基本域。度量曲面
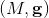同时为黎曼面，假设其全纯微分群的基底为
,
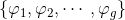由此我们构造所谓的周期矩阵
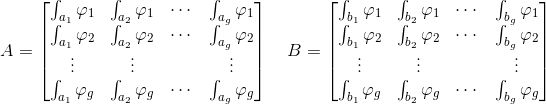
如此得到
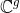中的格点群
,
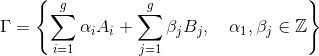这里
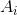是A周期矩阵的列向量，
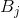是B周期矩阵的列向量，
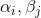都是整数。商空间
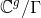被称为是黎曼面
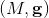的雅可比簇
。
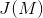从黎曼面到雅可比簇的Abel-Jacobi映射
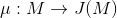被定义为：
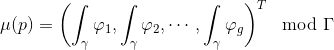
这里
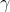是定义在基本域中，联结某个固定基点
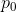和
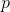的一条路径。
假如
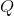是
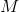的一个四边形网格剖分，我们将每个四边形面视作一个单位正方形，如此得到一个黎曼度量，称为由四边形网格诱导的度量，记为
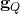。如果四边形网格的质量够高，则每个四边形的胞腔都接近和平面正方形相似，即四边形诱导度量和初始度量共形等价。在下面的讨论中，我们假设四边形网格的质量很高。
我们将四边形网格的奇异点用所谓的除子（Divisor）来表达，
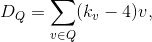
这里
是四边形网格的顶点，
是顶点的拓扑度，
被称为是顶点的阶（order）。如果
小于4，
被称为极点；如果
大于4，则
被称为零点。除子的Abel-Jacobi映射的像定义为：
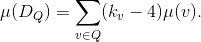
同样，给定亚纯微分
，其除子定义为形式和：
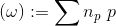
这里
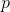是亚纯微分的零点或极点，
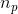是亚纯微分在
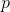点处的阶。
四边形网格奇异点构型的Abel条件可以表达为等式：
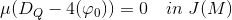
即在雅可比簇中，四边形网格奇异点构型
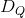的Abel-Jacobi映射的像等于任意一个全纯微分除子的Abel-Jacobi像的4倍。
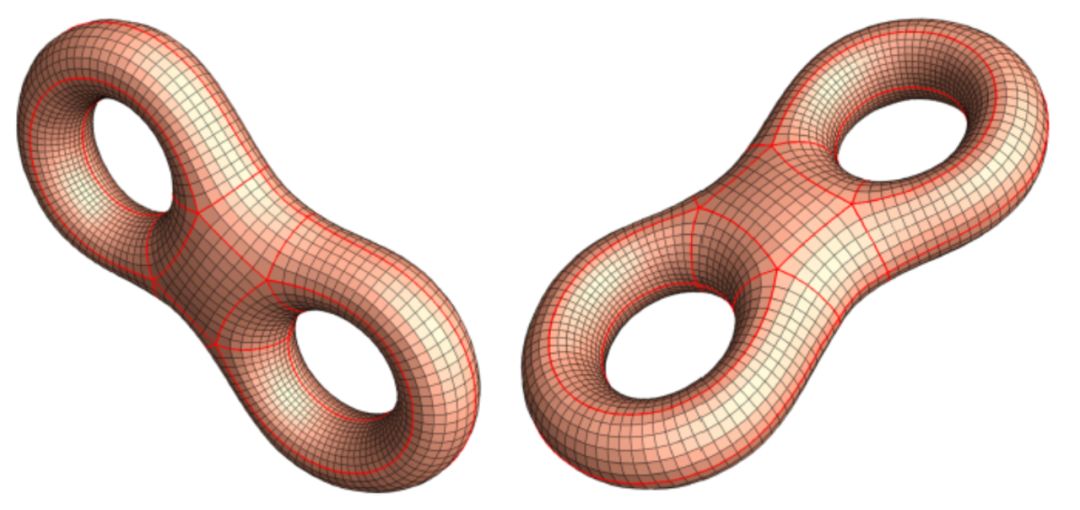
图7. 数值实验，输入亏格为二的四边形网格
图8. 数值实验，全纯1-形式基底
我们验算了高亏格曲面四边形网格的Abel条件，拓扑度为3的顶点为简单极点，拓扑度为5的顶点为简单零点，数值计算结果和理论预测完美吻合。
