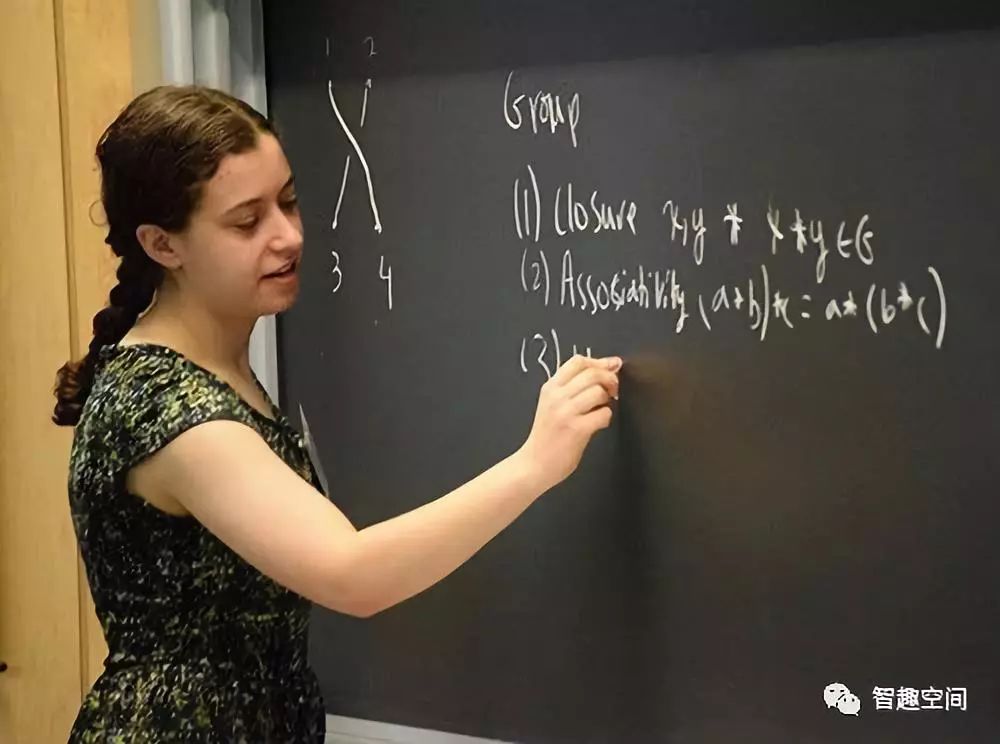
“群”
的概念是现代代数中伟大的思想之一,还是物理学中一个不可或缺的工具。这个概念曾经被Jame R.Newman比作英国作家卡罗尔著名童话故事《爱丽丝漫游奇境记》中柴郡猫的呲牙一笑。

代数课上,老师总是这样讲:当猫的身体消失不见时,只留下了一个让人琢磨不透的微笑。这一笑表明有什么有趣的事情发生了。如果我们不把群太当回事儿,也许群的概念就不那么神秘了。
说到群,大家感觉离自己太远了。其实,最近好些大家耳熟能详的益智玩具里面都包含这样的概念。比如:15 puzzle、魔方。

这个游戏的知名度是因为最强大脑而起,虽然国外它非常出名。当然这仅仅是因为在中国同为滑块游戏的华容道名气要比它大的多,而这个由美国萨姆劳埃德推出的移动十五游戏,现在也逐渐进入了国人的视野。
在15!=1*2*3*··· *15=1 307 674 368 000种排列组合中,正好一半的排列(即所谓的偶排列)是可以到达的状态,用数学的语言来说,这种滑动形成的排列就是一个
交代群
A
15
.
注:
S
n
中偶置换的全体构成一个1/2(n!)阶的子群,记作A
n
,称为交代群。

如果你熟悉三阶魔方,你会知道6个中心块,12个棱块和8个角块的概念。很多人复原魔方会用到白色中心块所在的面为底面。一个魔方的六个面上都有一块相当于不动的中心块。
我们以中心块作为定点,当双手拿着一个复原好的魔方放置在眼前的时候,我们可以知道单纯顶部和底部的旋转不改变顶部和底部色块与中心块的相对位置关系;转动前面或者后面,则将改变四个角块与中心块的相对位置;而如果再旋转左右面则将会改变四个角块和四个棱块与对应中心块的位置。
由于每次翻转都涉及偶数条边,于是,我们可以知道,对于魔方的任一可能状态来说:
边的翻转总数恒为偶数
又由于每次旋转都会产生相等数量角块的顺时针方向与逆时针方向的扭曲,所以:
角块上的扭曲总数总是按模3同余于0.
我们对角块的扭曲数记数时,把顺时针向的扭曲取为+1,逆时针向的取为-1,我们就能看到任意一个角块3次扭曲就回到原来的位置了,咱们可以看做一个一个被三等分的圆,每次转过120°,三次之后等于最原始的位置。
最后,魔方的滑动也和移动十五(大家都叫“数字华容道”)一样,是所谓的偶置换,我们可以想象它是可以通过偶数次对调来完成的。
所有20个角块和棱块总的置换必然是偶置换.
今天,我们的主题和辫子有关,同时也和数学有关,说到辫子,更多人可能脑海浮现的都是麻花辫,当然你想的是下图的样子,那也没关系的。

首先,隆重欢迎我们今天的主角:辫群。
辫子随处可见!珠宝、美发和许多装饰物都使用编织图案。


辫子也被研究作为数学对象,因为它们的数学结构是非常丰富和深刻的。辫群的第一个定义是两个平行圆盘之间的股线的集合。 辫子被认为是相同的,如果它们可以彼此变形而不切断辫子和保持两端点位固定(辫群同位素)。
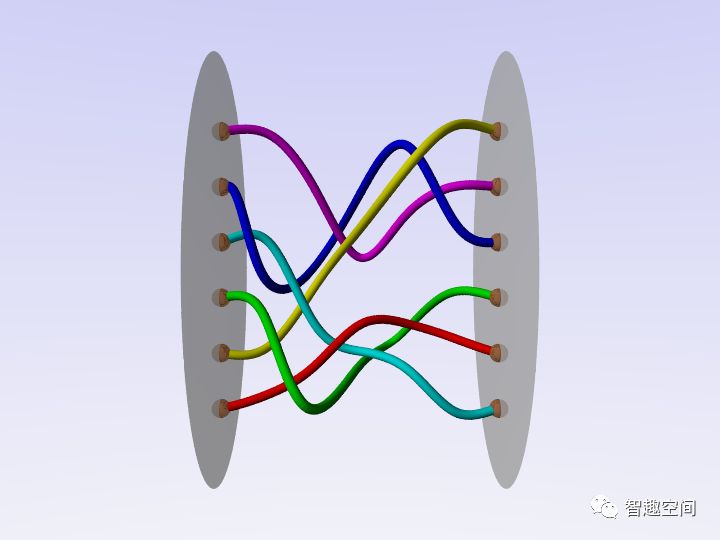
可以将两个辫子连接起来,得到一个新的辫子。这个操作被称为合成,并给出具有固定链数的辫子组的组结构。
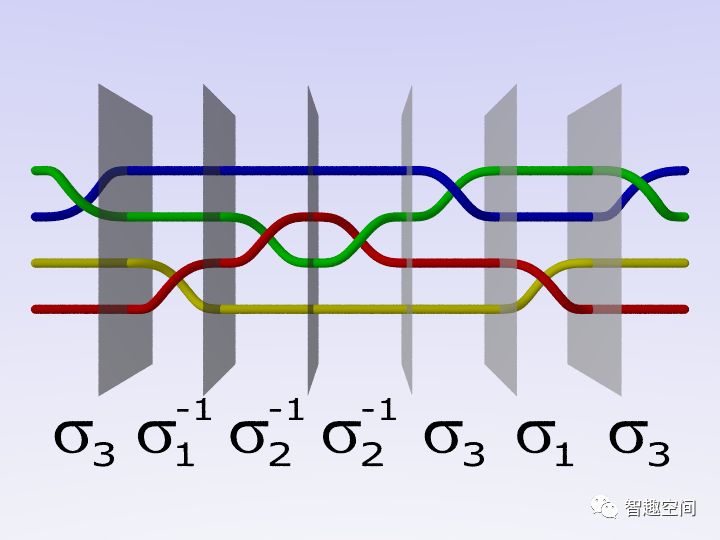
基本辫子是那些只有一个十字交叉的辫子。任何编织物都可以看作是基本辫子的组成,因此可以用一个词来描述。
下面是一个辫子群的Emil Artin示意图:

如果以上的部分,你看的一脸懵逼。那是因为咱们还没有给大家介绍开胃的游戏:
父母和孩子一家三口现在在玩儿一个游戏,首先,在一张白纸上画三条竖线,孩子自己在线条的一头随意标上A、B、C三个字母,然后把标有字母的部分折到后面,不要被父母看到哦!
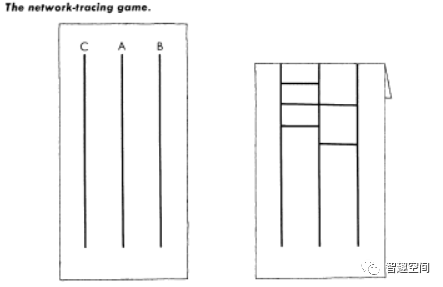
第二个人随意的在3条竖线之间画上一些横线,使得每条横线能和其中的两条竖线相连。最后一个人再加上一些横线,然后在其中一条竖线的地步标上字母 X .
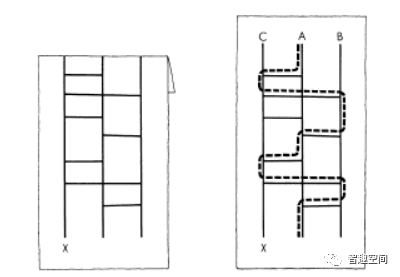
接下来,小朋友从A开始沿着竖线向下,碰到横线的一端时,(横线与竖线交叉位置忽略不计)沿着横线继续走到横线另一端后沿着竖线继续向下,直到遇见下一条横线的端头,如此反复直到走到底部。我们看到上图中,A并没有走到
X
的位置,
现在,该第二个人走这个画线游戏了,如果第二个是父亲,恭喜他,他就是为家庭服务的使者,可以是刷完,可以是其他任务,这个就由大家自己来决定啦!
刚才我们玩儿的游戏就是一个最简单的群,即3个符号的排列群。到底"群"是什么呢?
它是一个抽象的结构,包括一组没有明确定义的元素
(a,b,c,···
)
和一个没有明确定义的二进制运算(这里用
o
表示),这个运算使其中的一个元素与另一个元素结合产生了第三个元素。只有满足以下4个特点,这个抽象结构才能称之为“群”。
这四个特点分别是:
-
这组元素中的两个元素经过运算后,产生的结果是同组中的另外一个元素。这被称为“封闭性”;
-
这个运算遵循“结合律”:(a
o
b)
o
c=a
o
(b
o
c)
-
这组元素中有一个元素 e (叫做“单位元素”)符合a
o
e = e
o
a
-
对于任意元素 a 都对应一个逆元素 a‘ ,符合a
o
a' = a'
o
a = e
除了以上4个特点,如果运算还遵守交换律(a
o
b = b
o
a ),这样的群就叫做交换群或阿贝尔群。
如果你想跟我说你对群一无所知的话,其实我们在小学就学过一个群,就是关于加法运算的整数(正数、负数和零)的群。
加法运算的整数群是封闭的(
任一整数加上另一整数还是一个整数
),还符合结合律(
2+(3+4)=(2+3)=4
),群中有一个
单位元素
0,而且正整数的
逆元素就是他们相应的负数。
刚才咱们说了4个特点之外,如果还遵循交换律的话,那么我们可以吧加法运算的整数群叫做
阿贝尔群
。
留一个题目给读者:除法运算的整数具备一个群的特点吗?
再让我们回到家庭可以玩儿的那个画线游戏,这个游戏到底怎么体现了群的结构呢?

注:上图可以让孩子自行填一下每个圆圈内应该是什么顺序的排列?
咱们可以看到,A\B\C三个英文字母的排列组合一共有六种情况,意味着无论如何添加或者减少横线,结果无非就是这六种情况之一。
如果这个游戏你已经足够了解了,你可以试着验证一下是不是符合群的四个特点,是不是一个阿贝尔群呢?
我自己第一次看到这样一个游戏的时候,当时并没有关注马丁加德纳的第三本书,看到竟然无论如何添置横线,结果都不会让上面的线路最后走到同一个终点上,觉得这个游戏无比神奇。
现在让大家自行验证一下,通过表格里面的不同组合,咱们看看每两种元素的叠加后结果是什么?

同时,给大家提供一张游戏棋盘,大家自行打印覆膜后,就可以用完再擦掉了。

如果我们把刚才的画线游戏,变成给一个小女孩编三股的麻花辫,我们还能用群论来解释我们正在做的这件事情吗?
答案是肯定的,而且在我们之前的文章里面出现过的物理学家皮亚特·海因就用硬纸板做了这样一个不同寻常的游戏。
(注:用木片或者重一点的东西来做更好,一根长绳子也好于三根绳子的操作。)
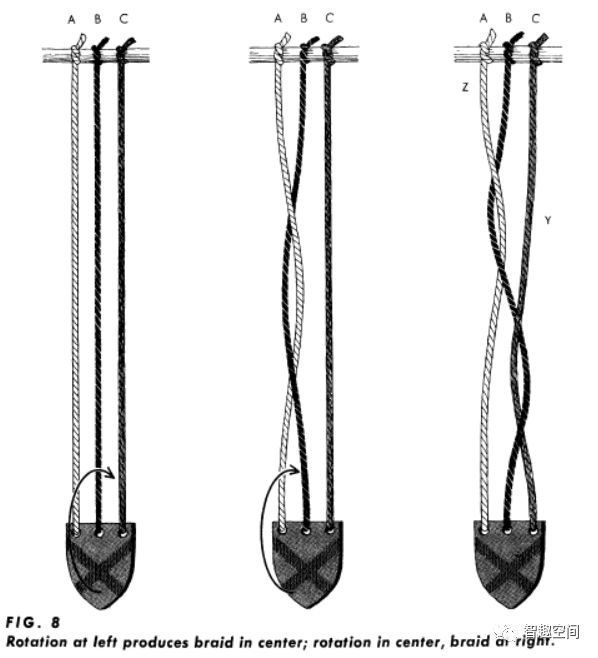
如上图所示,盾形的牌子两面要容易区分开来,比如像上图中一面画上
X
。
你用六种不同的方式旋转小牌子,就能编出6种不同的花样。咱们可以看出上图把盾牌沿着箭头先在B、C之间旋转,然后再在A、B之间旋转后就是最后一张图的样子。
20世纪30年代初,玻尔理论物理研究所的一次会议上,皮亚特·海因第一次听到埃伦·菲斯特把这个定理和量子论中的问题结合起来套路你,他们一起做了一个示范。之后海因又改进了这个游戏,绳子两头都系上一个小牌子就能形成一个对称的模型了,用这样的模型,两个人就可以玩一个拓扑游戏。
一人拿一个小牌子,把3根绳子抻直,两人轮流操作,一个人编辫,另一个人解开。计时,最快解开的人获胜。这个游戏后来就被叫做“Tangloids”。
因为解开它比你想象的简单,但是操作却比想象的更难想,而且在某些不熟悉的情况下你可能不知道该怎么解开。所以我们给出了一个制作一个这个游戏的图示方法,希望大家可以自行去做一个,实际体验一下游戏的效果。
下面是这个游戏的一个最终完成图:

首先,找到所需材料:






如何制作请自行脑补,最终,你就可以用它来验证你的猜测和操作是否完全对应了。


转偶数圈(每次旋转为任意方向)形成的辫子,不用再通过旋转小牌子就可以解开。转奇数圈的辫子就永远解不开了。
奇偶定理也可以应用到这个两人游戏中,初学者先限定为旋转的两圈编法,然后随着技术的不断提高,再按偶数的倍数增加。为什么转奇数圈和偶数圈有这么大的差别呢?这样的问题就留给大家自己去考虑了。
三根绳子已经够难了,所以四根绳子的游戏就不折磨大家了。

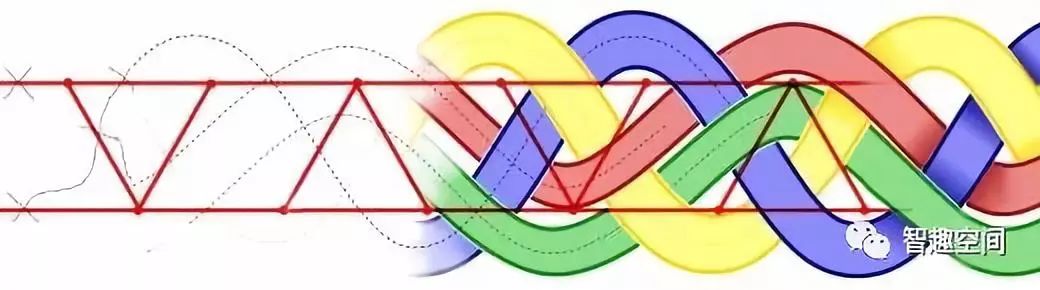
纽结论的应用更多,最有趣的是应用于DNA 链状结构的重新组合的研究。大家都知道DNA 的双链结构。这个长长的双链紧缩在细胞核里当然有很多纽结。有些酶的作用就是把链的某些地方断开,重新组合。这种重新组合可能会产生新的纽结,也可能去掉原来的纽结。搞清楚某些酶的工作机制很重要(某些病毒就是靠与DNA 组合来工作的)。数学家们利用数学中的纽结理论来研究DNA,从而搞清某些酶的工作机制,用到纽结论中很深刻的定理。数学的魔力再次展现。

-
参考资料:
-
马丁加德纳——《剪纸、棋盘游戏及堆积球》;















