关注上海房价的人都知道,市区又旧又破的老公房能卖到10来万,而许多郊区高大上的新房才只能卖到4万多。说起来,这其实是一个非常简单而重要的道理:
房子最重要的属性,就是区位(location)。
但仅仅是“区位”两个字,包含的东西有很多:到市中心的距离、临江临水、就业机会、人口密度、地铁、公交、商业、学校、医院……房价,很大程度上就是由这些要素决定的。
道理我们都懂,但从技术角度上看,区位对于房价的贡献度到底是怎样的呢?进一步说:
我们可以通过各种区位信息来模拟或预测一个未来开发地区的房价吗?
最近,我们针对上海的二手房价格,做了一个针对以上问题的研究。
首先,为了统一区位研究的空间单元,我们把上海划分为7000余个1km*1km的正方形格子。
其中,只有1000多个格子里是含有商品住宅的,因此,我们就选取了这1000多个格子作为样本对二手房均价进行模型的训练和验证。这1000多个格子在上海地图上的分布如下图所示,颜色越红表示房价越高(灰色区域是没有房子的6000个格子)。
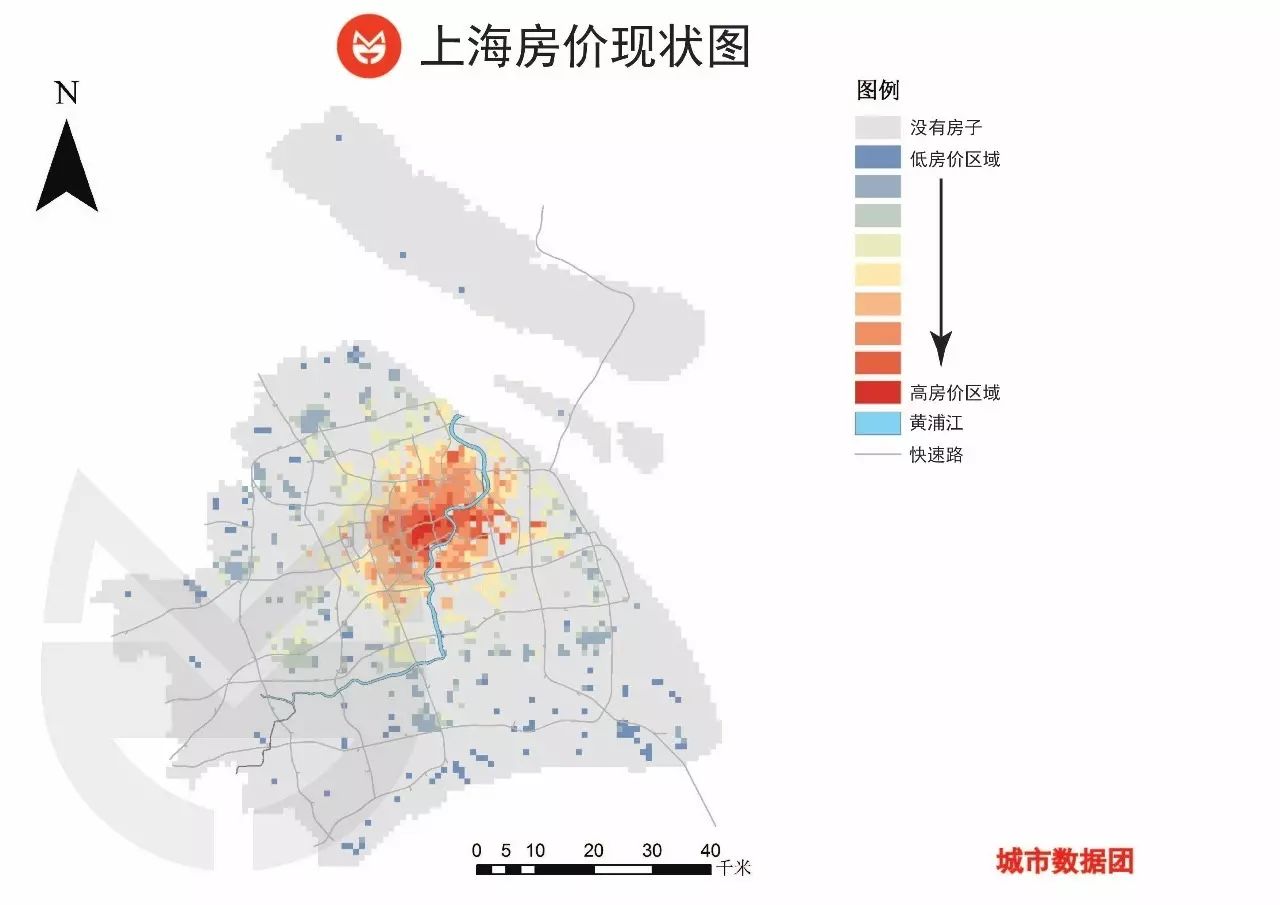
接下来,我们要开始准备数据了。
我们收集整理了每个格子的二手房均价、以及跟区位有关的3大类共26个特征要素,包括:
-
地理位置类(5个):到市中心及城市重要发展轴线的距离。
-
公共服务设施类(10个):本格子中的地铁站、加油站、学校等各种公共服务设施点的分布密度,以及受周边的影响情况。
-
城市要素类(11个):本格子日间人口、夜间人口、商业量等要素的分布密度,以及受周边的影响情况。
这些特征将会被我们纳入到房价预测的模型中。但是,它们的原始数据并不尽如人意,需要进行
预处理
后才能放进模型。
举一些例子吧:这些特征有的包含有异常值(远高于平均水平的样本)、有的数值分布极不均匀(分布形态不符合预期)、有的量级差异极大(如每个格子的地铁站数量往往只有个位数,而人数则以千或万作为量级)。与之相应的,预处理的流程包括去除异常值、降低分布的偏态系数、归一化等方法。
通过预处理把数据清洗得比较干净以后,我们要开始建立一个评判模型准确性的
检验机制
了。
我们需要把这1000个样本格子分为两部分:75%用于训练模型(训练样本),25%用于检验效果(验证样本)。这便是俗称的交叉验证法:用训练样本得到的模型对验证样本的房价进行预测,并与其实际价格进行比较。我们以均方根误差(缩写为RMSE)和误差率作为检验指标。
在完成这些麻烦的准备工作后,我们终于可以开始训练模型了。
我们选用的第一个模型是
Lasso回归
。
了解这个模型的同学们之后,这是一个普通最小二线性回归模型的升级版,其特征是在计算残差时加入了一个惩罚系数,而作用是抑制共线性对于回归模型的影响。
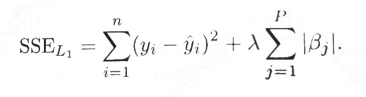
(标注1: Kuhn, Max, and K. Johnson. Applied Predictive Modeling. Springer New York, 2013. p.124)
惩罚系数的确定是模型根据RMSE的变化来自动确定的。在我们的模型中,当惩罚系数的参数项λ为0.9时,RMSE最小(如下图所示)。
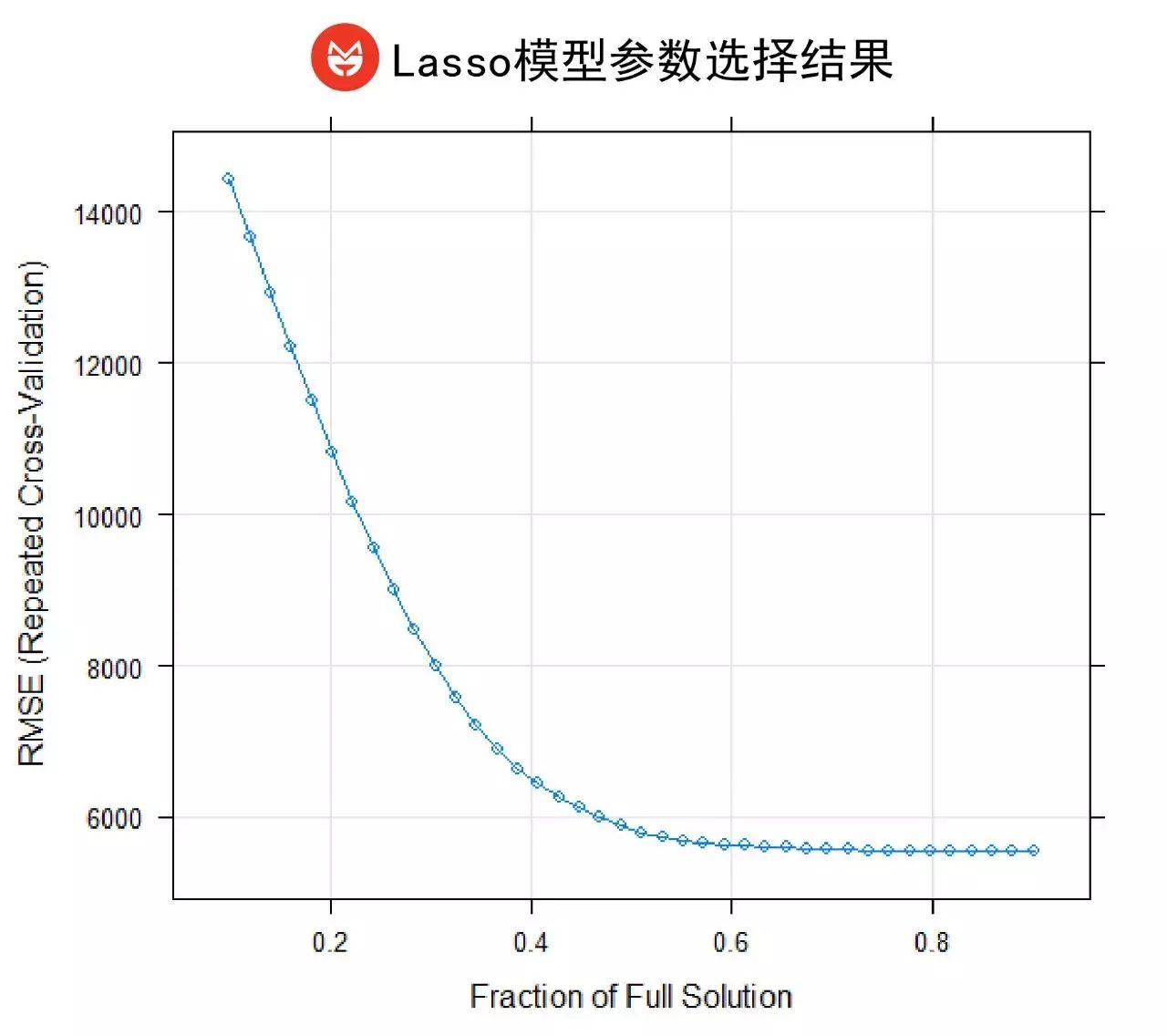
我们把λ=0.9代入Lasso模型中,并进行了验证。模型表现如下:

可以看到,预测结果的平均误差是4335元,误差率为9.8%。换句话说,当我们预测某个地区的房价时,很有可能会出现接近一成价格的偏差。这样的结果并不能令我们特别满意。
于是我们换了个模型——
偏最小二乘回归法(PLS
)。
这个模型可以简单地理解为监督学习版本的主成分回归。模型会根据均方根误差值的变化,提取出最合适的成分构成回归模型。在本研究中,当成分数为15时,RMSE最小并保持稳定。
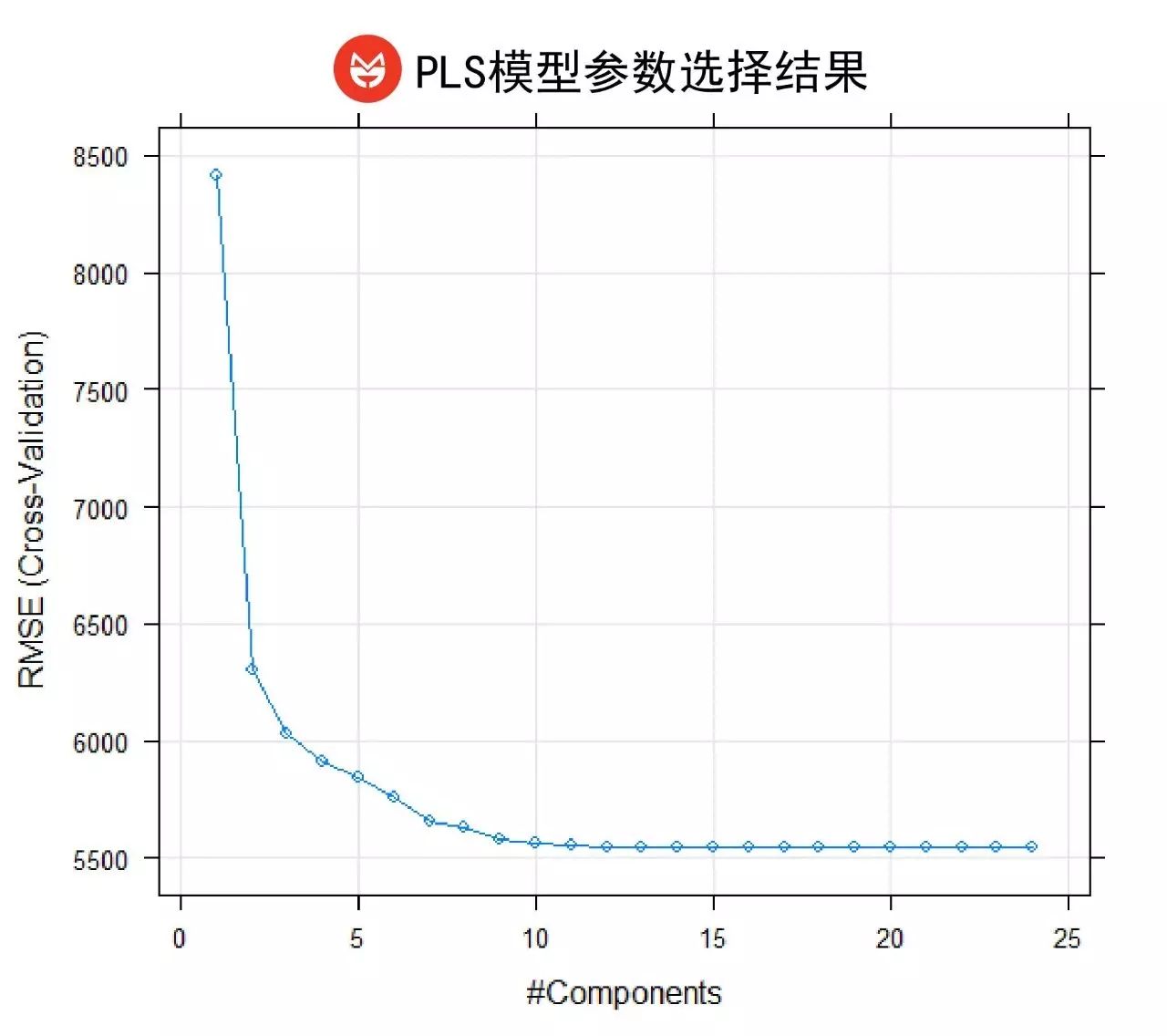
采用15个成分的PLS模型结果如下:

嗯……效果似乎并没有什么提升。
但我们是不会这么轻易放弃的。再试一次吧。我们觉得分段线性模型——
MARS模型
可能会更准一些。
这个模型会遍历每个特征的每个样本点,自动寻找最佳的分段点并构成回归模型。MARS模型也是一个典型的监督学习模型,其分段点和分段数都是模型根据RMSE的变化自动确定的。如图所示,我们的模型选取了17作为模型的分段数。
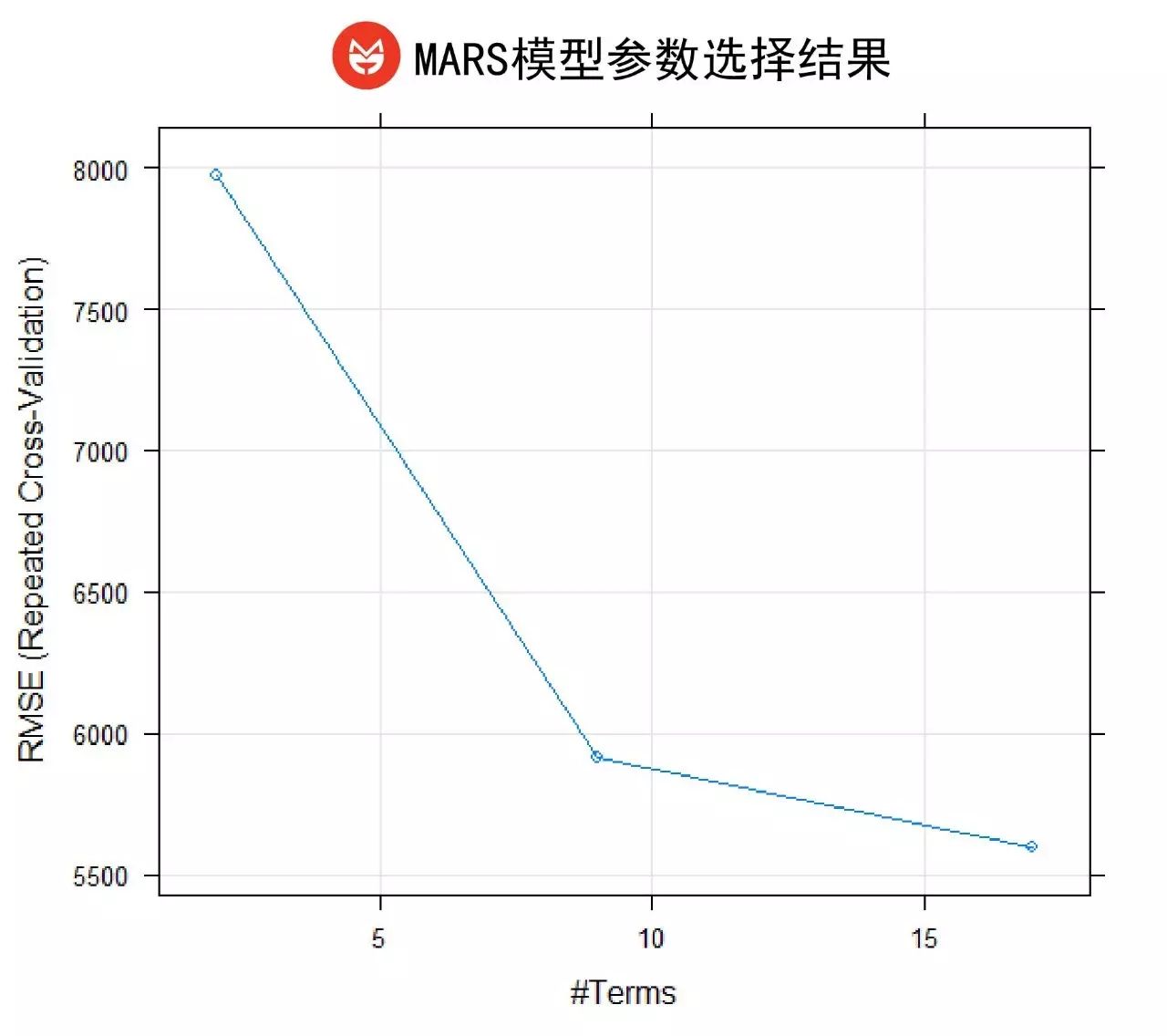
模型结果如下图所示:

嗯?……误差率不仅没有下降,居然还提高了。
好吧,看来我们必须祭出更加强大的“杀器”了!
我们先用一下同学们耳熟能详的
随机森林
吧。
随机森林是集成学习模型的代表,其大致的工作原理可以理解为,模型每次随机选取一部分的特征对一定量的样本构建回归树进行预测,每棵回归树拿自己的预测结果“投票”,最终模型选取“得票”最高的结果作为最终的输出结果。因为每棵回归树选取的特征是随机的且不同的,因此随机森林对于多元共线性并不敏感。
如图,模型自动决定每一次选取10个特征来构建回归树。
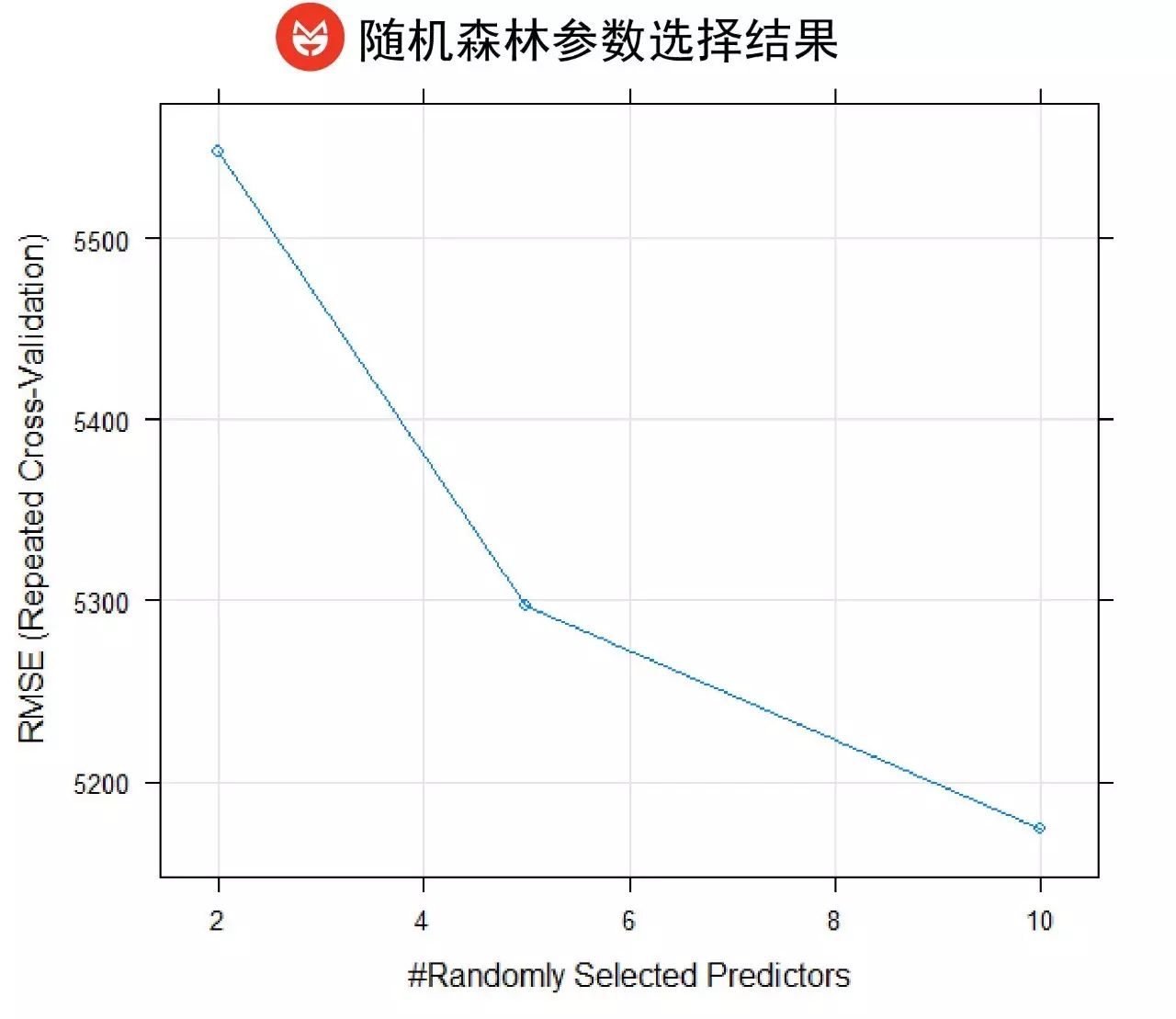
随机森林模型的结果如下图所示:

可以看到,均误差方根降低了整整500元,均误差率也从9.9%降到了8.6%。随机森林发挥了自己的威力,这不能不说这是一次可喜的进步。
但是,我们不能就此满足。
接下来出场的是新一代的集成学习模型——
Xgboot
。
该模型由华盛顿大学的陈天奇提出,具有很高的预测性和运行效率。由于原理比较复杂,在此就不详述了。运行一下就可以看到,xgboot模型使得我们的房价预测的准确率进一步提升了。请看下表:

使用了Xgboot模型的结果比随机森林的结果,误差率更低,下降到了8%。
至此,我们一共使用了5个模型,准确率最高可达92%。这就是用区位特征预测房价的极限了吗?
秉着精益求精的精神,我们决定引入
集成学习
的策略,综合不同预测模型的优势,从而获得更加准确的预测结果。
集成学习的方法有很多, 我们选取的是“Stacking”学习法:
将第一轮训练中得到的5个模型的预测结果作为新的特征构成新的数据集(现在我们有31个特征了),使用新的数据集重新训练模型并进行检验,从而使前序学习的有效结果也能够参与到新学习的贡献当中,以选取出表现最好的模型。
在第二轮的预测中,我们只选用了第一轮预测的优胜者:随机森林和Xgboot两个模型,结果如下图所示:

可以看到,通过集成学习,两个模型的均误差方根与第一轮相比都降低了10个以上的百分点。相对而言,Xgboot模型的表现要更好一些,其均误差方根仅为3286元,误差率降到了7.1%。换句话说,最后被我们集成出的这个模型的准确率高达
93%
!
最后,让我们回顾一下这次用区位特征预测房价的工作吧。
我们用1000个样本的平均价格和用第二轮Xgboot模型预测得到的误差值画成下面这张图(纵坐标表示误差值,若圆点的纵坐标越接近0,说明误差越小,预测得越准确):
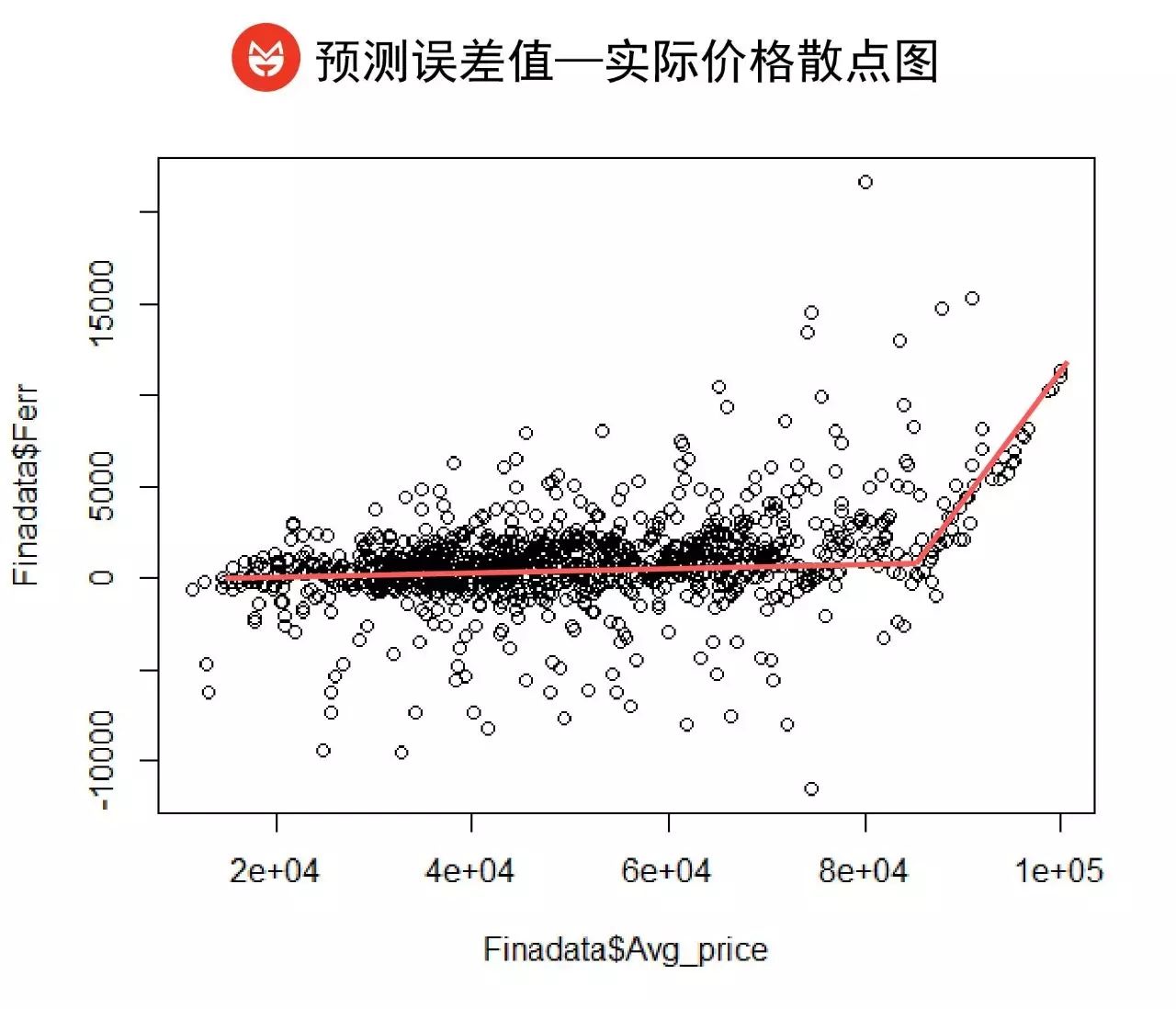
可以看到,在我们准确度高达93%的模型中,对8万元以下区域的房价均价预测是相当准确的,整个效果非常收敛。
但相比之下,它对于8万元以上土豪城区和豪宅区的价格预测结果就没有那么理想了。究其原因,我们猜想这可能是因为高价值地段的房屋样本太少,也可能是因为高价值地段的房子具有更多地理区位以外的附加价值:越是豪宅,可能越不完全依赖区位。
到这里,我们的房价预测基本完成了。但是,我们仅仅对上海市域内1000平米土地上的房价进行了预测,那剩下的6000平米土地呢?
虽然这些地方现在没有房子,但也许未来会有呢?如果这些地方未来建成了新房,大概会在什么价位呢?
我们把训练出的模型应用到全市,对全市7000个格子的房子的房价进行了预测。结果见下图:
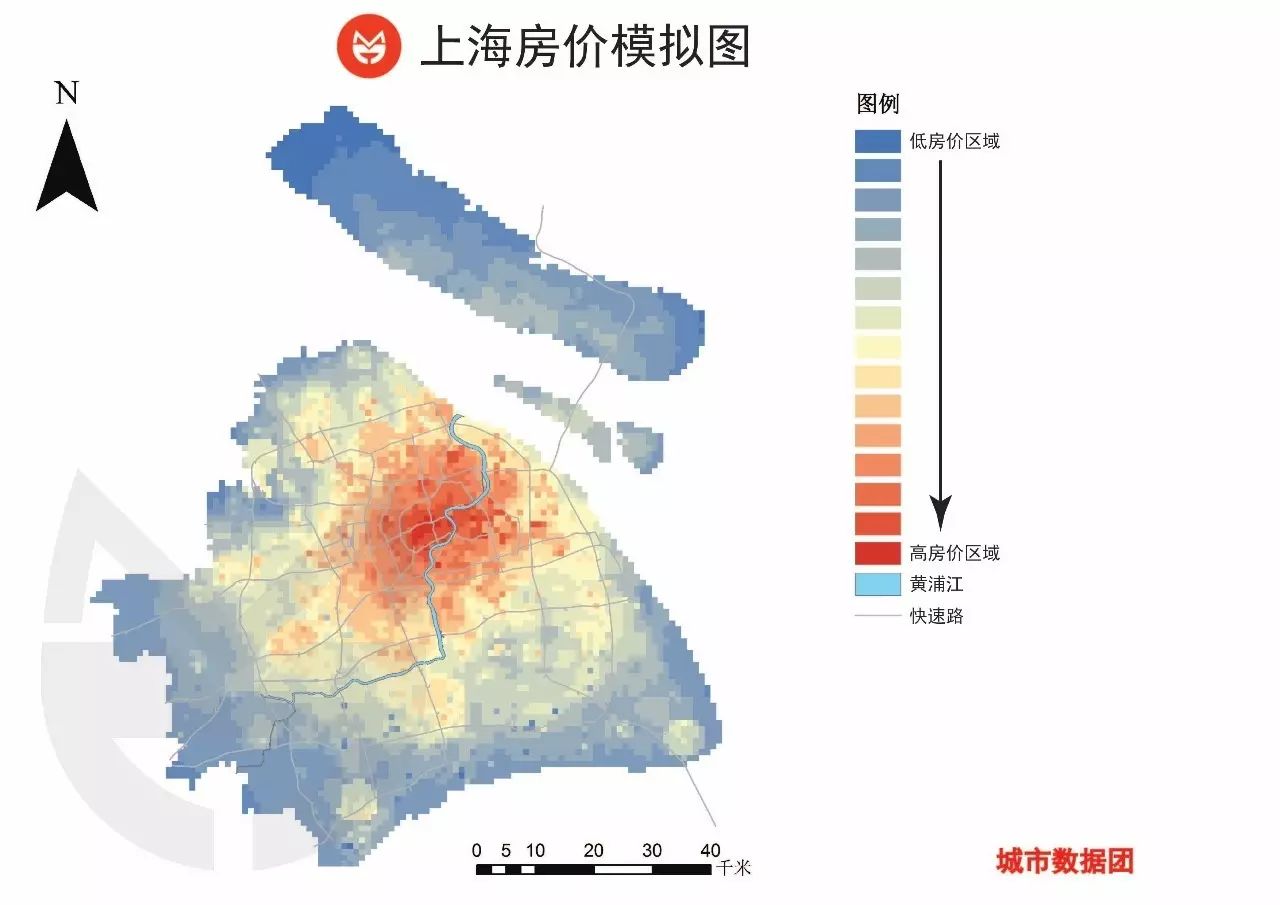
在这张图上,随着离市中心的距离增加,房价呈圈层状逐渐向外递减,但在嘉定、青浦、松江、奉贤等部分新城有所提升。这也符合我们的经验认知。
我想,科学的价值就是在此:即使是复杂如城市和房价,也应该有其规律可言的吧。而我们需要做的则是,从纷繁复杂的数据中,通过模型与技术,不断地把这些规律挖掘出来,使之更接近这个世界的真相。
当然,由于本次研究采用的是2017年年初的截面数据,收集到的房屋样本量和城市特征要素的种类也都不是特别多,以及研究者的水平有限,预测模型的准确性和可靠性还有进一步提升的空间。接下里,我们将在新的时间截面上不断地跟进此类研究,在更长的时间周期内对模型进行验证与调优工作。
也欢迎志同道合的小伙伴们加入我们。
说明:
-
本研究由 阮田 完成,团支书 协助文字整理。本文由微信公众号 城市数据团 原创并首发。
-
本文中使用的数据由 脉策数据 提供。
-
由于涉及商业机密,我们对研究中涉及的具体参数、算法和结果进行了模糊处理或未予展示,请各位读者谅解。





