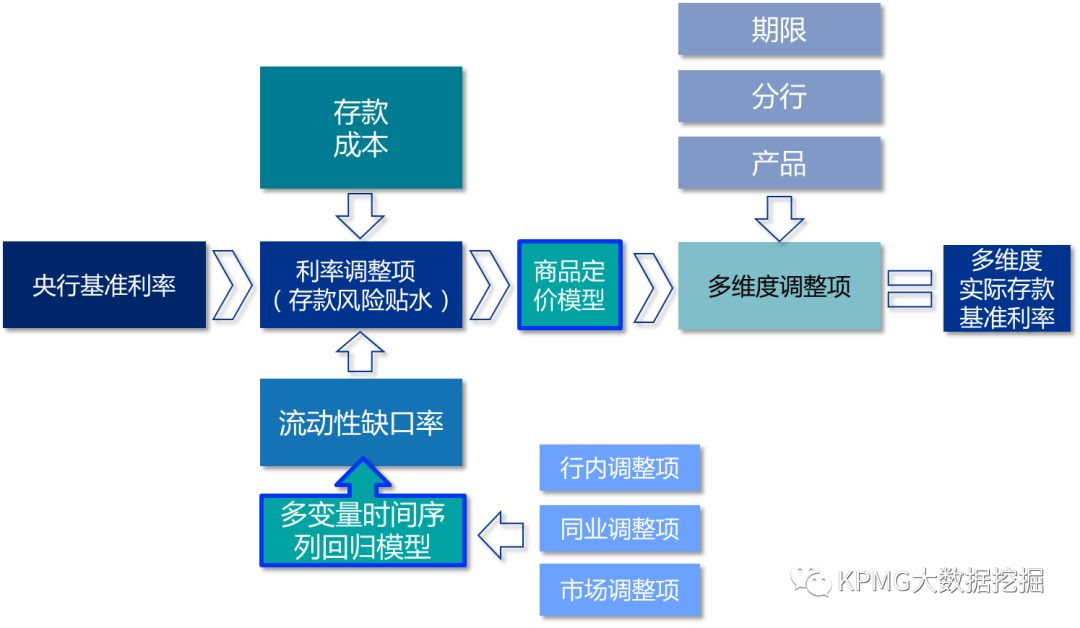
我们先看看存款利率定价的模型架构和分类:
01
商品定价模型
利率是存款的价格。运用蒙特卡罗模拟法是假设利率的价格变动服从某种随机过程的形态,随机路径是被一个随机利率模型决定。例如股价变动过程的主要特征为随机、不为负值及向上漂移等;利率过程特别需要建置具有均数复归特性的随机过程;能源价格则需要一个可以将均数复归和跳跃纳入考量的价格过程,以解释偶尔发生的价格飙涨。籍由电脑模型,产生几百次、几千次,甚至几万次可能价格的路径,并依次建构投资组合的报酬分配,进而推估其风险值。
蒙特卡罗模拟法是一种基于大数法则的实证方法,当实验的次数越多,它的平均值也就会越趋近于理论值。
结合金融商品无套利均衡理论,银行存款定价模型如下,di(t)是利率微分的表达式,即为本期与上一期利率的差额作为最终预测的目标值,利用差额微积分的方法可以将利率的局部的变化率描述成一种线性特征。
已知当期的存款利率,和预测的利率的差额,可以利用模型的微分表达式预测出未来一期甚至多期的利率。
因此,在理想情况下即为情况一,差额为0,市场上不存在套利的空间,投资在银行的金额得到的回报率与投资在市场上无风险金融商品的回报率相同,而在实际情况下,各种银行金融机构还是存在资金缺口,需要通过存款的风险贴水吸引存款弥补缺口,而实际市场上也不存在完全的无风险金融商品,即使接近无风险的国债也存在一定的风险贴水,因此需要通过情况二下的模型对利率进行存款的定价,将存款的风险贴水与市场上投资商品的金融风险考量进来,即商品定价模型。
|
情况一:理想情况下,无资金缺口
在无资金缺口的情况下,我们需要考虑的参数有国债收益率曲线r(t)、央行存款利率i(t)以及客户对利率的敏感性k,从而计算当期与上一期的利率差值。
|情况二:现实情况下,有资金缺口
在现实情况下,由于需要考虑资金缺口的问题,因此要新增
风险贴水
γ
和
存款风险贴水
μ
两个变量,作为对收益率及存款利率的调整。
02
多维度的调整项
以央行基准利率为基础,考量多变量时间序列回归模型产出的利率调整项,放入商品定价模型,再分多维度产出不同的时间存款基准利率。存款利率的维度分为三个层级,分别是期限,分行和产品,层级间相互独立。
期限
:定存产品的时间期限别
产品
:依据行内产品进行区分
分支行
:根据各行实际情况和颗粒度要求不同,考虑各分支机构的业务目标和地域差异作为划分依据。
由于维度有三层,在处理多变量时间序列回归模型或者是商品定价模型的时候需要考量到每一个维度的情况,区别作出调整,如在分行层级的情况下,在全行下,宏观变量为全国区域的宏观变量,但是在地域分行下,宏观变量为地域的宏观变量。
利率的多维度调整的基本处理方式
是以全行的变量指标(宏观、同业、行内、成本)为基础参考变量,宏观指标由全国指标对应到各分行对应的地域指标。
同业指标
由各分行提供的对标行作为对应地域的同业金融机构的参考,若分行无明确的对标行,则使用其余对标行的平均水平;行内指标包含成本则采取每一家分行的行内对应管理指标和每一家分行的行内成本。
不同的数据来源存在数据积累不全面,长度不一致,频率不齐全等问题,
在各家银行存款定价模型中的输入数据需保持维度、结构、长度及频率全部一致,方可以获得最准确完整的存款利率结果。
03












