【香樟推文0843】失落的美国梦

一代宗师中宫二小姐说习武之人有三个阶段：见自己，见天地，见众生。说的是除了自身条件及努力之外，还有更多的因素在影响着个人的发展。机会，就是其中最重要的因素之一。尤其是对于年轻人来说，能够在更注重个人能力的地方通过自身努力实现经济和社会地位的跃升，会极大地左右其就业和居住选择，因此机会常常被看作社会活力的象征。但是，不平等问题的出现使得人们对所在地能够提供给自己的发展机会产生了怀疑。今天推送的这篇文章介绍了曾经被认为是自由之地的美国，在1940年之后经历的代际流动性的急剧下降。

代际流动性是指子女和父母之间收入和受教育程度的相关性，而本文通过测算绝对收入流动性来衡量代际流动。绝对收入流动性指子女中收入超过父母的人数的比例，以此表示子女实现了经济地位的跃升，如果绝对收入流动性越高，社会机会就越均等。在基础测算中，通过对比1940-1942年出生的小孩在30岁左右（即1970-1972）时的绝对收入流动性以及1980-1982年出生的小孩在30岁左右（即2011-2012）时的绝对收入流动性来看是否出现了绝对收入流动性的下降。本文最大的难点在于历史数据的缺失，要对比1940出生的小孩和1980年出生的小孩的绝对收入流动性，就必须要有1940年有小孩的父母的收入数据以及1970年小孩的收入数据，而实际可获得的数据并没有1970年之前出生人口的跟踪调查数据，因此成为本文测算的难点。下文就逐步介绍衡量绝对收入流动性的指数的构造方法以及数据处理方法，以及在此基础上本文的稳定性检验和基本结论。

绝对收入流动指数衡量的是在某个时期中如1940-1942年所有的出生人口在30年后其收入超过父母收入的人口比重，所以绝对收入流动指数可以直观地构造为公式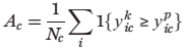（1）：

  (1)

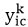表示在出生组C中的第i个小孩的收入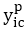，表示在出生组c中的小孩i父母的收入。公式表明如果出生组C中小孩的收入大于他们的父母，则记为1。Nc为出生组C中小孩的总数，可以看出AC即为在收入上实现了跃升的小孩的比例。因此，AC即表示出生组c中的绝对收入流动指数，如当C=1940时，AC表示出生在1940年的小孩在30岁时相比他们的父母所实现的绝对收入流动：AC越高，则绝对收入流动越多，社会机会越均等。

如何计算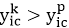个数呢？本文分别利用父母和小孩收入边缘概率分布以及通过copula函数（也称连接函数）构建的联合概率分布来计算AC，具体可写为：

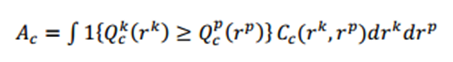(2)

其中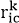，表示小孩i的收入在出生组c中所有小孩组成的收入分布中的百分位排名，相应地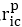表示小孩i的家长在出生组c中所有孩子家长组成的收入分布中的百分位排名。进一步，用

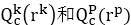
来分别表示处于出生组C中小孩和家长在各自的收入百分位排名下的用美元表示的收入。可知，如果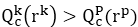则实现了绝对收入的代际流动，可记为1，而这种情况发生的概率为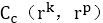。至此，我们只要知道在每个出生组中选取为样本的父母和孩子的边缘收入分布，利用copula函数构建在同一出生组的父母和孩子收入的联合概率分布，就可以计算Ac了。

计算方法解决后，Ac的计算还需要同一出生组中父母和孩子各自收入的边缘分布。现实情况是，1970年的人口普查数据（CPS）可以得到在20世纪80年代出生的小孩的父母在30岁时的收入数据，以及30年后这些小孩收入的追踪数据，但是1970年之后没有相应的追踪数据。因此，不知道1940-1942出生的小孩他们的父母在30岁时的收入分布数据（因为没有追踪数据，所以不知道1970-1972年时30岁的人，他们的父母是谁，他们的父母在30年前生他们的时候是多少岁，这就造成了估计得出20世纪40年代出生组中父母与孩子收入联合分布的困难）。本文为得到这个收入分布，提出了一个前提假设即：1940之后，任意出生组的copula函数是基本稳定的（本文通过copula函数定义父母收入和孩子收入的联合分布），基于此估计。

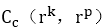为了估计那些在1970-1972年时孩子已经30岁的父母的收入边缘分布，本文利用1940-1942的混合数据（pool data）来计算这些父母在30岁时的收入分布。比如如果选择的出生组是1970年，而不知道这个出生组中孩子父母的收入边缘分布，于是这样选择：首先，利用1970年人口普查数据得到那些在1970年年龄为25-35岁的在当时拥有小于一岁的孩子的人为父母；然后到1980年的人口普查数据中选取在当时年龄为26-35的拥有年龄为10岁的孩子的人为父母（即在1970年的时候这些人年龄为16-25岁并且拥有年龄小于1岁的孩子）；最后，转到1960年的人口普查数据，找到年龄为25-35岁的人（到1970年的时候他们就为35-45岁的人），并用1970年人口普查中年龄为35-45并且拥有年龄小于1岁的孩子的人在总人口中的比重来乘以1960的数据。这样就可以同时找到那些在2000-2002年拥有30岁孩子的父母的在25-35岁时的收入。为什么要选择年龄为25-35岁的人呢，因为如果只在1970年选择年龄为30岁的人作为孩子的父母的样本数据，那么不一定能包括在那一年生孩子所有的父母，而25-35是关于30岁呈对称分布的年龄区间。至此，我们就在缺少面板数据的情况下得到了估计，估计20世纪40年代出生组中父母收入边缘分布的方法，以及在copula函数一致性假设下相应1940-1970孩子和父母收入的联合分布。

本文的基本估计是计算1940-1942年出生组的孩子和父母在30岁时绝对收入流动指数（A1940-1942）和1980-1982年出生组的孩子和父母在30岁时绝对收入流动指数（A1980-1982），并进行对比以观察绝对收入流动性是否出现变动。文章的基本结果是1940年之后，绝对收入流动性急剧下降，特别是对于中产阶级家庭来说。对于那些父母收入处于其收入分布中10%百分位排名的孩子来说，如果他出生在1940年则他的收入有94%的可能超过他的父母，而如果他出生在1980年则他的收入只有70%的可能超过他的父母；对于那些父母收入处于其收入分布中50%百分位排名的孩子来说，如果他出生在1940年则他的收入有93%的可能超过他的父母，而如果他出生在1980年则他的收入只有45%的可能超过他的父母；对于那些父母收入处于其收入分布中90%处百分位排名的孩子来说，他如果出生在1940年则他的收入有88%的可能超过他的父母，而如果他出生在1980年则他的收入只有33%的可能超过他的父母。

由于之前提出的假设——在1940之后，任意出生组的copula函数是基本稳定的这个条件并不一定满足，本文还利用边界分析，即通过选择copula函数的界来估算，具体可参照原文。

本文对结果的稳定性和异质性进行了进一步分析。在验证结论稳健性时，本文对衡量收入的指标利用不同的通货膨胀指标进行了计算，得到1980年代的绝对收入流动性有提高但是变化非常小；然后利用不同的价格指数对收入进行计算，同样对绝对收入流动指数的影响非常小；本文还将孩子和父母的收入对比年龄由30岁改为40岁，得到的结果依然稳健。总体来说，1940年之后绝对收入流动性是出现了大幅下降的。然后本文对结果进行了异质性检验。看看在不同的子样本下，绝对收入流动是否出现了相同的下降。首先，文章对不同的州的绝对收入流动进行计算，发现在美国的50个州中，绝对收入流动都出现了下降，但是在美国中西部工业城市的绝对收入流动出现了更大的下降，在曼彻斯特、纽约等城市的绝对收入流动下降的幅度较小；其次，本文还对性别异质性进行了检验，发现在孩子为男性的家庭中，绝对收入流动下降幅度较大，1940年出生的男孩有95%的可能性收入超过他们的父母而1984年出生的男孩只有41%的可能收入超过其父母；而孩子为女生的家庭，1940年出生的女孩有43%的可能收入超过他们的父母，而1984年出生的女孩有26%的可能收入超过其父母，下降幅度较小。

在稳健性检验和异质性检验中可以知道，总体来说，美国绝对收入流动出现了普遍的大幅的下降。

本文利用反事实分析方法对绝对收入流动性下降的原因进行了进一步的分析。本文认为1940-1980年出现绝对流动性下降的同时美国出现了GDP增速下降和收入差距扩大的基本事实，对这两个基本事实进行反事实分析发现：如果在保持收入分配不变，而提高GDP增速对1980年的绝对收入流动性进行在测算发现绝对收入流动为62%，而之前测算的为50%；而如果保持GDP增速不变，将收入分配变为1940年的水平重新测算绝对收入流动发现为80%。可知，在这个角度来看，收入分配不公是引起绝对收入流动性下降的更重要的原因。

至此，可知本文主要得到两个结论：第一，1940年之后，孩子想要比他们的父母挣得更多更难了；其二，绝对收入流动性降低的主要原因在于收入分配的不公平。曾经实现梦想的黄金热土也不免成为梦想失落的之地，而作者认为改变这一境况的当务之急是将增长带来的好处实现更加公平的分配。