
肖仰华:复旦大学计算机科学技术学院,副教授,博士生导师,上海市互联网大数据工程技术中心副主任。
主要研究方向为大数据管理与挖掘、知识库等。
大数据时代的到来,为人工智能的飞速发展带来前所未有的数据红利。在大数据的“喂养”下,人工智能技术获得了前所未有的长足进步。其进展突出体现在以知识图谱为代表的知识工程以及深度学习为代表的机器学习等相关领域。随着深度学习对于大数据的红利消耗殆尽,深度学习模型效果的天花板日益迫近。另一方面大量知识图谱不断涌现,这些蕴含人类大量先验知识的宝库却尚未被深度学习有效利用。融合知识图谱与深度学习,已然成为进一步提升深度学习模型效果的重要思路之一。以知识图谱为代表的符号主义、以深度学习为代表的联结主义,日益脱离原先各自独立发展的轨道,走上协同并进的新道路。
大数据为机器学习,特别是深度学习带来前所未有的数据红利。得益于大规模标注数据,深度神经网络能够习得有效的层次化特征表示,从而在图像识别等领域取得优异效果。但是随着数据红利消失殆尽,深度学习也日益体现出其局限性,尤其体现在依赖大规模标注数据和难以有效利用先验知识等方面。这些局限性阻碍了深度学习的进一步发展。另一方面在深度学习的大量实践中,人们越来越多地发现深度学习模型的结果往往与人的先验知识或者专家知识相冲突。如何让深度学习摆脱对于大规模样本的依赖?如何让深度学习模型有效利用大量存在的先验知识?如何让深度学习模型的结果与先验知识一致已成为了当前深度学习领域的重要问题。
当前,人类社会业已积累大量知识。特别是,近几年在知识图谱技术的推动下,对于机器友好的各类在线知识图谱大量涌现。知识图谱本质上是一种语义网络,表达了各类实体、概念及其之间的语义关系。相对于传统知识表示形式(诸如本体、传统语义网络),知识图谱具有实体/概念覆盖率高、语义关系多样、结构友好(通常表示为RDF格式)以及质量较高等优势,从而使得知识图谱日益成为大数据时代和人工智能时代最为主要的知识表示方式。能否利用蕴含于知识图谱中的知识指导深度神经网络模型的学习从而提升模型的性能,成为了深度学习模型研究的重要问题之一。
现阶段将深度学习技术应用于知识图谱的方法较为直接。大量的深度学习模型可以有效完成端到端的实体识别、关系抽取和关系补全等任务,进而可以用来构建或丰富知识图谱。本文主要探讨知识图谱在深度学习模型中的应用。从当前的文献来看,主要有两种方式。一是将知识图谱中的语义信息输入到深度学习模型中;将离散化知识图谱表达为连续化的向量,从而使得知识图谱的先验知识能够成为深度学习的输入。二是利用知识作为优化目标的约束,指导深度学习模型的学习;通常是将知识图谱中知识表达为优化目标的后验正则项。前者的研究工作已有不少文献,并成为当前研究热点。知识图谱向量表示作为重要的特征在问答以及推荐等实际任务中得到有效应用。后者的研究才刚刚起步,本文将重点介绍以一阶谓词逻辑作为约束的深度学习模型。
知识图谱是人工智能符号主义近期进展的典型代表。知识图谱中的实体、概念以及关系均采用了离散的、显式的符号化表示。而这些离散的符号化表示难以直接应用于基于连续数值表示的神经网络。为了让神经网络有效利用知识图谱中的符号化知识,研究人员提出了大量的知识图谱的表示学习方法。知识图谱的表示学习旨在习得知识图谱的组成元素(节点与边)的实值向量化表示。这些连续的向量化表示可以作为神经网络的输入,从而使得神经网络模型能够充分利用知识图谱中大量存在的先验知识。这一趋势催生了对于知识图谱的表示学习的大量研究。本章首先简要回顾知识图谱的表示学习,再进一步介绍这些向量表示如何应用到基于深度学习模型的各类实际任务中,特别是问答与推荐等实际应用。
知识图谱的表示学习旨在学习实体和关系的向量化表示,其关键是合理定义知识图谱中关于事实(三元组< h,r,t >)的损失函数 ƒ
r
(h,t),其中和是三元组的两个实体h和t的向量化表示。通常情况下,当事实 < h,r,t > 成立时,期望最小化 ƒ
r
(h,t)。考虑整个知识图谱的事实,则可通过最小化
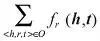
来学习实体以及关系的向量化表示,其中 O 表示知识图谱中所有事实的集合。不同的表示学习可以使用不同的原则和方法定义相应的损失函数。这里以基于距离和翻译的模型介绍知识图谱表示的基本思路[1]。
基于距离的模型。
其代表性工作是 SE 模型[2]。基本思想是当两个实体属于同一个三元组 < h,r,t > 时,它们的向量表示在投影后的空间中也应该彼此靠近。因此,损失函数定义为向量投影后的距离
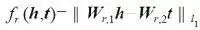
其中矩阵 W
r,1
和 W
r,2
用于三元组中头实体 h 和尾实体 t 的投影操作。但由于 SE 引入了两个单独的投影矩阵,导致很难捕获实体和关系之间的语义相关性。Socher 等人针对这一问题采用三阶张量替代传统神经网络中的线性变换层来刻画评分函数。Bordes 等人提出能量匹配模型,通过引入多个矩阵的 Hadamard 乘积来捕获实体向量和关系向量的交互关系。
基于翻译的表示学习。
其代表性工作 TransE 模型通过向量空间的向量翻译来刻画实体与关系之间的相关性[3]。该模型假定,若 < h,r,t > 成立则尾部实体 t 的嵌入表示应该接近头部实体 h 加上关系向量 r 的嵌入表示,即 h+r≈t。因此,TransE 采用

作为评分函数。当三元组成立时,得分较低,反之得分较高。TransE 在处理简单的 1-1 关系(即关系两端连接的实体数比率为 1:1)时是非常有效的,但在处理 N-1、1-N 以及 N-N 的复杂关系时性能则显著降低。针对这些复杂关系,Wang 提出了 TransH 模型通过将实体投影到关系所在超平面,从而习得实体在不同关系下的不同表示。Lin 提出了 TransR 模型通过投影矩阵将实体投影到关系子空间,从而习得不同关系下的不同实体表示。
除了上述两类典型知识图谱表示学习模型之外,还有大量的其他表示学习模型。比如,Sutskever 等人使用张量因式分解和贝叶斯聚类来学习关系结构。Ranzato 等人引入了一个三路的限制玻尔兹曼机来学习知识图谱的向量化表示,并通过一个张量加以参数化。
当前主流的知识图谱表示学习方法仍存在各种各样的问题,比如不能较好刻画实体与关系之间的语义相关性、无法较好处理复杂关系的表示学习、模型由于引入大量参数导致过于复杂,以及计算效率较低难以扩展到大规模知识图谱上等等。为了更好地为机器学习或深度学习提供先验知识,知识图谱的表示学习仍是一项任重道远的研究课题。
应用 1
问答系统。自然语言问答是人机交互的重要形式。深度学习使得基于问答语料的生成式问答成为可能。然而目前大多数深度问答模型仍然难以利用大量的知识实现准确回答。Yin 等人针对简单事实类问题,提出了一种基于 encoder-decoder 框架,能够充分利用知识图谱中知识的深度学习问答模型[4]。在深度神经网络中,一个问题的语义往往被表示为一个向量。具有相似向量的问题被认为是具有相似语义。这是联结主义的典型方式。另一方面,知识图谱的知识表示是离散的,即知识与知识之间并没有一个渐变的关系。这是符号主义的典型方式。通过将知识图谱向量化,可以将问题与三元组进行匹配(也即计算其向量相似度),从而为某个特定问题找到来自知识库的最佳三元组匹配。匹配过程如图 1 所示。对于问题 Q:“How tallis Yao Ming?”,首先将问题中的单词表示为向量数组 H
Q
。进一步寻找能与之匹配的知识图谱中的候选三元组。最后为这些候选三元组,分别计算问题与不同属性的语义相似度。其由以下相似度公式决定:
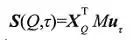
这里,S(Q,τ) 表示问题Q 与候选三元组τ 的相似度;x
Q
表示问题的向量( 从H
Q
计算而得),u
τ
表示知识图谱的三元组的向量,M是待学习参数。
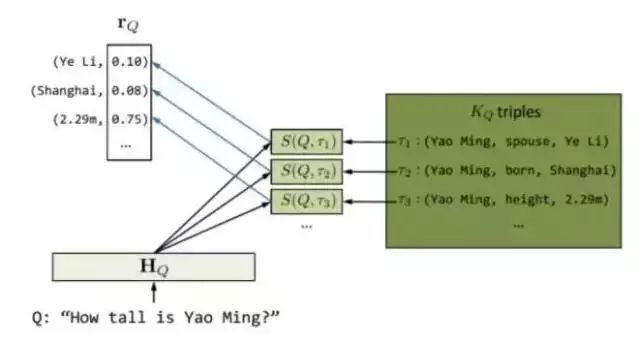
图1 基于知识图谱的神经生成问答模型
应用 2
推荐系统。
个性化推荐系统是互联网各大社交媒体和电商网站的重要智能服务之一。随着知识图谱的应用日益广泛,大量研究工作意识到知识图谱中的知识可以用来完善基于内容的推荐系统中对用户和项 目的内容(特征)描述,从而提升推荐效果。另一方面,基于深度学习的推荐算法在推荐效果上日益优于基于协同过滤的传统推荐模型[5]。但是,将知识图谱集成到深度学习的框架中的个性化推荐的研究工作,还较为少见。Zhang 等人做出了这样的尝试。作者充分利用了结构化知识(知识图谱)、文本知识和可视化知识(图片)[6]等三类典型知识。作者分别通过网络嵌入(network embedding)获得结构化知识的向量化表示,然后分别用SDAE(Stacked Denoising Auto-Encoder)和层叠卷积自编码器(stackedconvolution-autoencoder)抽取文本知识特征和图片知识特征;并最终将三类特征融合进协同集成学习框架,利用三类知识特征的整合来实现个性化推荐。作者针对电影和图书数据集进行实验,证明了这种融合深度学习和知识图谱的推荐算法具有较好性能。
Hu 等人提出了一种将一阶谓词逻辑融合进深度神经网络的模型,并将其成功用于解决情感分类和命名实体识别等问题[7]。逻辑规则是一种对高阶认知和结构化知识的灵活表示形式,也是一种典型的知识表示形式。将各类人们已积累的逻辑规则引入到深度神经网络中,利用人类意图和领域知识对神经网络模型进行引导具有十分重要的意义。其他一些研究工作则尝试将逻辑规则引入到概率图模型,这类工作的代表是马尔科夫逻辑网络[8],但是鲜有工作能将逻辑规则引入到深度神经网络中。
Hu 等人所提出的方案框架可以概括为“teacher-student network”,如图 2 所示,包括两个部分 teacher network q(y|x) 和 student network p
θ
(y|x)。其中 teacher network 负责将逻辑规则所代表的知识建模,student network 利用反向传播方法加上teacher network的约束,实现对逻辑规则的学习。这个框架能够为大部分以深度神经网络为模型的任务引入逻辑规则,包括情感分析、命名实体识别等。通过引入逻辑规则,在深度神经网络模型的基础上实现效果提升。
 图2 将逻辑规则引入到深度神经网络的
图2 将逻辑规则引入到深度神经网络的
“teacher-student network”模型
其学习过程主要包括如下步骤:
利用 soft logic 将逻辑规则表达为 [0, 1] 之间的连续数值。
基于后验正则化(posterior regularization)方法,利用逻辑规则对 teacher network 进行限制,同时保证 teacher network 和 student network 尽量接近。最终优化函数为:

其中,ξ
l,gl
是松弛变量,L 是规则个数,G
l
是第 l 个规则的 grounding 数。KL 函数(Kullback-Leibler Divergence)部分保证 teacher network 和student network 习得模型尽可能一致。后面的正则项表达了来自逻辑规则的约束。
对 student network 进行训练,保证 teacher network 的预测结果和 student network 的预测结果都尽量地好,优化函数如下:
 其中,t 是训练轮次,l 是不同任务中的损失函数(如在分类问题中,l 是交叉熵),σ
θ
是预测函数,s
n
(t)
是 teacher network 的预测结果。
其中,t 是训练轮次,l 是不同任务中的损失函数(如在分类问题中,l 是交叉熵),σ
θ
是预测函数,s
n
(t)
是 teacher network 的预测结果。
重复 1~3 过程直到收敛。
随着深度学习研究的进一步深入,如何有效利用大量存在的先验知识,进而降低模型对于大规模标注样本的依赖,逐渐成为主流的研究方向之一。知识图谱的表示学习为这一方向的探索奠定了必要的基础。近期出现的将知识融合进深度神经网络模型的一些开创性工作也颇具启发性。但总体而言,当前的深度学习模型使用先验知识的手段仍然十分有限,学术界在这一方向的探索上仍然面临巨大的挑战。这些挑战主要体现在两个方面:
如何获取各类知识的高质量连续化表示。当前知识图谱的表示学习,不管是基于怎样的学习原则,都不可避免地产生语义损失。符号化的知识一旦向量化后,大量的语义信息被丢弃,只能表达十分模糊的语义相似关系。如何为知识图谱习得高质量的连续化表示仍然是个开放问题。
如何在深度学习模型中融合常识知识。大量的实际任务(诸如对话、问答、阅读理解等等)需要机器理解常识。常识知识的稀缺严重阻碍了通用人工智能的发展。如何将常识引入到深度学习模型将是未来人工智能研究领域的重大挑战,同时也是重大机遇。
参考文献
[1] 刘知远, 孙茂松, 林衍凯, 等. 知识表示学习研究进展[J]. 计算机研究与发展, 2016, 53(2):247-261.
[2] Bordes A, Weston J, Collobert R, et al. Learning Structured Embeddings of KnowledgeBases[C]// AAAI Conference on Artificial Intelligence, AAAI 2011, SanFrancisco, California, Usa, August. DBLP, 2011.
[3] Bordes A, Usunier N, Garcia-Duran A, et al. Translating Embeddings for ModelingMulti-relational Data[J]. Advances in Neural Information Processing Systems,2013:2787-2795.
[4] Jun Yin, Xin Jiang, Zhengdong Lu,Lifeng Shang, Hang Li, Xiaoming Li, NeuralGenerative Question Answering. IJCAI2016.
[5] Giovanni Semeraro , Pasquale Lops , Pierpaolo Basile, Knowledge infusion intocontent-based recommender systems: ACM Conference on Recommender Systems, 2009.
[6] Fuzheng Zhang, Nicholas Jing Yuan, Defu Lian, Xing Xie, Wei-Ying Ma, Collaborative Knowledge Base Embedding for Recommender Systems, in Proc. of KDD, 2016.
[7] Hu, Z., Ma, X., Liu, Z., Hovy, E., & Xing, E. (2016). Harnessing deep neural networks with logic rules. arXiv preprint arXiv:1603.06318.
[8] Matthew Richardson and Pedro Domingos. 2006. Markov logic networks. Machine learning,62(1-2):107–136.
转载自中国人工智能学会通讯 2017 第 4 期
媒体合作请联系:
邮箱:[email protected]





